Дисперсия и среднее квадратическое отклонение случайной величины конспект

Обновлено: 07.07.2024

В теории вероятностей Дисперсия случайной величины Х называется математическое ожидание Е (Х — m_х) 2 квадрата отклонения Х от её математического ожидания m_х = Е (Х). Д. случайной величины Х обозначается через D (X) или через s 2 _X.

Для случайной величины Х с непрерывным распределением вероятностей, характеризуемым плотностью вероятности р (х), дисперсия вычисляется по формуле

Дисперсией (рассеянием)случайной величины называется математическое ожидание квадрата ее отклонения от ее математического ожидания:

Замечание 1. В определении дисперсии оценивается не само отклонение от среднего, а его квадрат. Это сделано для того, чтобы отклонения разных знаков не компенсировали друг друга.

Замечание 2. Из определения дисперсии следует, что эта величина принимает только неотрицательные значения.

Замечание 3. Существует более удобная для расчетов формула для вычисления дисперсии, справедливость которой доказывается в следующей теореме:

D(X) = M(X ²) – M ²(X). (7.7)

Используя то, что М(Х) – постоянная величина, и свойства математического ожидания, преобразуем формулу (7.6) к виду:

D(X) = M(X – M(X))² = M(X² - 2X·M(X) + M²(X)) = M(X²) – 2M(X)·M(X) + M²(X) =

= M(X²) – 2M²(X) + M²(X) = M(X²) – M²(X), что и требовалось доказать.

1) Дисперсия постоянной величины С равна нулю:

D (C) = 0. (7.8)

Доказательство. D(C) = M((C – M(C))²) = M((C – C)²) = M(0) = 0.

2) Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат:

D(CX) = C²D(X). (7.9)

Доказательство. D(CX) = M((CX – M(CX))²) = M((CX – CM(X))²) = M(C²(X – M(X))²) =

= C²D(X).

3) Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий:

D(X + Y) = D(X) + D(Y). (7.10)

Доказательство. D(X + Y) = M(X² + 2XY + Y²) – (M(X) + M(Y))² = M(X²) + 2M(X)M(Y) +

+ M(Y²) – M²(X) – 2M(X)M(Y) – M²(Y) = (M(X²) – M²(X)) + (M(Y²) – M²(Y)) = D(X) + D(Y).

Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме их дисперсий.

Следствие 2. Дисперсия суммы постоянной и случайной величин равна дисперсии случайной величины.

4) Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:

D(X – Y) = D(X) + D(Y). (7.11)

Доказательство. D(X – Y) = D(X) + D(-Y) = D(X) + (-1)²D(Y) = D(X) + D(X).

Дисперсия дает среднее значение квадрата отклонения случайной величины от среднего; для оценки самого отклонения служит величина, называемая средним квадратическим отклонением.

Средним квадратическим отклонением σ случайной величины Х называется квадратный корень из дисперсии:

Опр:Средним квадратическим отклонением (х) С.В.Х. называется число

Замечание:матем.ожидание М(х) характеризует среднее значение С.В.

Дисперсия D(x)характеризует квадратичное отклонение С.В. от среднего значения:

Св-ва D(x): 1)D(c)=0: 2)D(k*x)= *D(x)

Док-во:D(x)=M(x-M(x)) 2 )=M(x 2 -2x*M(x)+M 2 (x))=M(x 2 )-2M(x)*M(M(x))+M(M 2 (x))=M(x 2 )-2M(x)*M(x)+M 2 (x)=M(x 2 )-M 2 (x)

M(x) M 2 (X)-постоянные величины

Производящей функцией случайной величины x называется функция комплексного переменного z

производящая функцияпоследовательности f₀, f₁. f_n. функция

(в предположении, что этот степенной ряд сходится хотя бы для одного значения t ¹ 0). Производящая функцияназывают также генератрисой. Последовательность f₀, f₁. f_n. может быть как числовая, так и функциональная; в последнем случае Производящая функция зависит не только от t, но и от аргументов функций f_n. Например, если f_n= aq n где а и q - постоянные, то Производящая функция

если f_n - Фибоначчи числа; f₀ = 0, f₁ = 1, f_n+2= f_n+1+ f_n, то Производящая функция

если f_n = Т _n(х) - Чебышева многочлены: T₀(х)= 1, T_n (х)= cos (n arc cos x), то Производящая функция

и т.д. Знание Производящая функция последовательности часто облегчает изучение свойств последней. Производящая функция применяются в теории вероятностей, в теории функций и в алгебре (в теории инвариантов). Впервые метод Производящая функция был применен П. Лапласом для решения некоторых проблем теории вероятностей.

Названные числовые характеристики дают представление о разбросе случайных величин относительно их среднего значения.

Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

Для вычисления дисперсии можно использовать слегка преобразованную формулу

т.к. М(х), 2 и постоянные величины, то

Свойства дисперсии.

Свойство 1. Дисперсия постоянной равна нулю. По определению

Свойство 2. Постоянную можно выносить за знак дисперсии с возведением в квадрат.

Центрированной случайной величиной называется отклонение случайной величины от ее математического ожидания.

Центрированная величина обладает двумя удобными для преобразования свойствами:

Свойство 3. Если случайные величины Х и У независимы, то

Доказательство. Обозначим . Тогда и . Поэтому

Во втором слагаемом в силу независимости случайных величин и свойств центрированных случайных величин

поэтому равенство можно продолжить

Пример. Если a и b – постоянные, то D(ax+b)=D(ax)+D(b)=

Дисперсия, как характеристика разброса случайной величины, имеет один недостаток. Если, например, Х – ошибка измерения имеет размерность ММ, то дисперсия имеет размерность . Поэтому часто предпочитают пользоваться другой характеристикой разброса – средним квадратическим отклонением, которое равно корню квадратному из дисперсии.

Среднее квадратическое отклонение имеет ту же размерность, что и сама случайная величина.

Дисперсия числа появления события в схеме независимых испытаний.

Производится n независимых испытаний и вероятность появления события в каждом испытании равна р. Выразим, как и прежде, число появления события Х через число появления события в отдельных опытах

Так как опыты независимы, то и связанные с опытами случайные величины независимы. А в силу независимости имеем

Но каждая из случайных величин имеет закон распределения и , поэтому по определению дисперсии

Среднее квадратическое отклонение числа появления событий в n независимых опытах равно .

Моменты случайных величин.

Помимо уже рассмотренных случайные величины имеют множество других числовых характеристик.

Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени этой случайной величины.

Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени соответствующей центрированной величины.

Легко видеть, что центральный момент первого порядка всегда равен нулю, центральный момент второго порядка равен дисперсии, т.к. .

Центральный момент третьего порядка дает представление об асимметрии распределения случайной величины. Моменты порядка выше второго употребляются сравнительно редко, поэтому мы ограничимся только самими понятиями о них.

Числовые характеристики системы случайных величин составляют числовые характеристики каждой из величин, входящих в систему, и числовые характеристики, дающие представление о характере связи между величинами. Числовые характеристики каждой из величин по отдельности определяются как числовые характеристики обычных случайных величин. Из числовых характеристик зависимости между величинами назовем лишь наиболее употребимую.

15. Дисперсия и среднеквадратическое отклонение дискретных и непрерывных случайных величин; свойства дисперсии.

Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от своего математического ожидания

Для дискретной случайной величины дисперсия вычисляется по формуле

для непрерывной находят интегрированием

Если непрерывная величина заданная на интервале то дисперсия равна интегралу с постоянными пределами интегрирования

Для вычисления дисперсии можно использовать слегка преобразованную формулу

т.к. М(х), 2 и постоянные величины, то

Свойства дисперсии.

Свойство 1. Дисперсия постоянной равна нулю. По определению

Свойство 2. Постоянную можно выносить за знак дисперсии с возведением в квадрат.

Центрированная величина обладает двумя удобными для преобразования свойствами:

Свойство 3. Если случайные величины Х и У независимы, то

Доказательство. Обозначим . Тогда и . Поэтому

Во втором слагаемом в силу независимости случайных величин и свойств центрированных случайных величин

поэтому равенство можно продолжить

Пример. Если a и b – постоянные, то D(ax+b)=D(ax)+D(b)=

Среднее квадратическое отклонение имеет ту же размерность, что и сама случайная величина.

Дисперсия числа появления события в схеме независимых испытаний.

Но каждая из случайных величин имеет закон распределения и , поэтому по определению дисперсии

Среднее квадратическое отклонение числа появления событий в n независимых опытах равно .

Моменты случайных величин.

Помимо уже рассмотренных случайные величины имеют множество других числовых характеристик.

Для дискретной случайной величины дисперсия вычисляется по формуле

для непрерывной находят интегрированием

Закон распределения полностью характеризует случайную величину с вероятностной точки зрения. Однако при решении многих практических задач достаточно знать лишь некоторые Числовые параметры, выражающие наиболее характерные свойства (черты) закона распределения случайной величины. Такие числа носят название Числовых характеристик случайной величины.

Математическим ожиданием (или средним значением) (или ) дискретной случайной величины X называется сумма произведений всех ее возможных значений на соответствующие вероятности этих значений.

Если дискретная случайная величина X принимает конечное число значений , то ее математическое ожидание находится по формуле

Если же дискретная случайная величина X принимает бесконечное (счетное) число значений, то

При этом математическое ожидание существует, если ряд в правой части этой формулы абсолютно сходится, т. е. сходится ряд .

Математическое ожидание непрерывной случайной величины X с плотностью вероятности , находится по формуле

При этом математическое ожидание существует, если интеграл в правой части равенства абсолютно сходится (это значит, что сходится интеграл ).

Дисперсией (рассеянием) (или ) случайной величины Называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

Из определения вытекает часто используемая формула:

Если - Дискретная случайная величина, то ее дисперсия вычисляется по формуле:

В случае конечного числа значений, принимаемых случайной величиной X, и по формуле

В случае счетного числа значений.

Если X - непрерывная случайная величина С Плотностью , то

Средним квадратическим отклонением Случайной величины Называется величина .

Среднее квадратическое отклонение есть мера рассеяния значений случайной величины около ее математического ожидания.

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

11 класс.

Цели: определить алгоритм вычисления дисперсии ; формировать умение вычислять дисперсию и среднее квадратическое отклонение при решении задач.

I. Организационный момент.

II. Устная работа.

1. Для упорядоченных рядов найдите размах, среднее арифметическое, моду и медиану.

а) 0; 0; 1; 1; 2. б) 1; 2; 2; 3; 3; 4. в) 1; 2; 3; 4; 5; 6.

2. На гистограмме представлены данные о распределении рабочих цеха по возрастным группам:

Пользуясь гистограммой, найдите:

а) число рабочих цеха в возрасте от 18 до 48 лет;

б) возрастную группу, к которой относится наибольшее число рабочих;

в) общее число рабочих цеха.

III. Объяснение нового материала.

2. Рассматриваем пример 8 со с. 309 учебника. В нем проводится сравнение точности и надежности трех различных ружей, дается описательное определение того, за что, собственно, отвечает дисперсия.

На описательном уровне: если х ₁ , х ₂ , …, х _п – результаты измерения и М – их среднее значение, то дисперсия D вычисляется так:

D = .

Итак, дисперсия D результатов измерения равна среднему арифметическому квадратов отклонений этих результатов от их среднего значения. Если дисперсия D достаточно мала, то большинство ошибок измерения х _i – М невелики по модулю. Это значит, что числа х ₁ , х ₂ , …, х _п в основном довольно тесно группируются вокруг своего среднего значения М . В таком случае результаты, заметно отличающиеся от М , скорее всего следует отнести к ошибкам измерения. Другими словами, если D = 0, то х ₁ = х ₂ = … = х _п = М и, грубо говоря, если D  0, то х _i  М .

3. Затем выделяем алгоритм вычисления дисперсии (с. 311 учебника) и иллюстрируем этот алгоритм разбором ситуации, описанной в примере 8. Таким образом, это тот минимум, который нельзя пропустить при любом способе знакомства с такой важной числовой характеристикой как дисперсия.

IV. Формирование умений и навыков.

Возможно при решении этих задач использовать данные собственного класса. Задачи № 50.8 и № 50.9 можно выполнять по вариантам.

а) Выпишем сгруппированный ряд данных:

б) Составим таблицу распределения кратностей:

в) Вычислим процентные частоты: Построим многоугольник распределения процентных частот.

г) Вычислим среднее:

Ср = = 3,44.

а) Выпишем сгруппированный ряд данных:

б) Составим таблицу распределения кратностей:

в) Вычислим процентные частоты: Построим многоугольник распределения процентных частот

г) Вычислим среднее:

Ср = = 3,2.

а) Определим число итоговых двоек: 4;

б) Определим число итоговых пятерок: 5;

в) Составим таблицу распределения итоговых отметок. Для этого запишем ряд сумм отметок:

9, 9, 4, 7, 5, 6, 7, 8, 6, 3, 8, 6, 3, 8, 7, 7, 10, 8, 9, 4, 5, 7, 9, 5, 6.

Упорядочим ряд, сгруппировав по итоговой отметке:

г) Изобразим гистограмму распределения итоговых отметок.

Для решения данной задачи так же используем данные предыдущих трех задач.

а) Воспользуемся алгоритмом вычисления дисперсии.

1) Вычислим среднее значение отметок по литературе:

2) Вычислим отклонения данных от Ср и занесем в таблицу.

3) Вычислим квадраты отклонений и тоже внесем в таблицу.

4) Вычислим дисперсию как среднее значение всех квадратов отклонений.

D = =
= = 1,2864.

Среднее квадратичное  =  1,134.

б) Аналогично вычисляем дисперсию и среднее квадратичное отметок по русскому языку:

D = 1,12;   1,0583.

в) Анализируя полученные данные, получаем, что в среднем отметки выше по литературе.

г) Более устойчивый характер имеют отметки по русскому языку.

V. Итоги урока.

– Какая числовая характеристика отвечает за разброс (рассеивание) данных вокруг их среднего значения?

– Назовите алгоритм вычисления дисперсии.

– Как вычисляется среднее квадратическое отклонение? Что оно характеризует?

Итак, продолжаем. В предыдущей статье мы выяснили, насколько полезно знать математическое ожидание, однако только этой характеристики ещё не достаточно для исследования случайной величины. Представим двух стрелков, которые стреляют по мишени. Один стреляет метко и попадает близко к центру, а другой… просто развлекается и даже не целится. Но что забавно, его средний результат будет точно таким же, как и у первого стрелка! Эту ситуацию условно иллюстрируют следующие случайные величины:

Таким образом, возникает потребность количественно оценить, насколько далеко рассеяны пули (значения случайной величины) относительно центра мишени (математического ожидания). Ну а рассеяние с латыни переводится не иначе, как дисперсия.

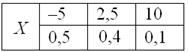
Посмотрим, как определяется эта числовая характеристика на одном из примеров 1-й части урока:

Там мы нашли неутешительное математическое ожидание этой игры, и сейчас нам предстоит вычислить её дисперсию, которая обозначается через .

–5 – (–0,5) = –4,5
2,5 – (–0,5) = 3
10 – (–0,5) = 10,5

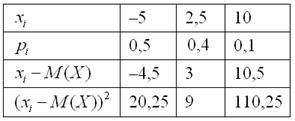
Чтобы обойти эту неприятность можно рассмотреть модули разностей, но по техническим причинам прижился подход, когда их возводят в квадрат. Решение удобнее оформить таблицей:

И здесь напрашивается вычислить средневзвешенное значение квадратов отклонений. А это ЧТО такое? Это их математическое ожидание, которое и является мерилом рассеяния:

– определение дисперсии. Из определения сразу понятно, что дисперсия не может быть отрицательной – возьмите на заметку для практики!

Иногда это значение называют стандартным отклонением.

В чём его смысл? Если мы отклонимся от математического ожидания влево и вправо на среднее квадратическое отклонение:

Во-первых, очевидно то, что при увеличении ставок, дисперсия тоже возрастает. Так, например, если мы увеличим в 10 раз, то математическое ожидание увеличится в 10 раз, а дисперсия – в 100 раз (коль скоро, это квадратичная величина). Но, заметьте, что сами-то правила игры не изменились! Изменились лишь ставки, грубо говоря, раньше мы ставили 10 рублей, теперь 100.

Второй, более интересный момент состоит в том, что дисперсия характеризует стиль игры. Мысленно зафиксируем игровые ставки на каком-то определённом уровне, и посмотрим, что здесь к чему:

То же самое происходит на Форексе, других биржах и так далее – примеров масса.

Наверное, вы заметили, что нахождение дисперсии – есть процесс длительный и кропотливый. Но математика щедрА:

Формула для нахождения дисперсии

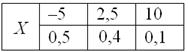
Данная формула выводится непосредственно из определения дисперсии, и мы незамедлительно пускаем её в оборот. Скопирую сверху табличку с нашей игрой:

и найденное матожидание .

Вычислим дисперсию вторым способом. Сначала найдём математическое ожидание – квадрата случайной величины . По определению математического ожидания:

В данном случае:

Таким образом, по формуле:

Как говорится, почувствуйте разницу. И на практике, конечно, лучше применять формулу (если иного не требует условие).

Осваиваем технику решения и оформления:

Дискретная случайная величина задана своим законом распределения:

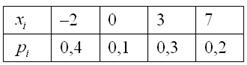
Найти её математическое ожидание, дисперсию и среднее квадратическое отклонение.

Эта задача встречается повсеместно, и, как правило, идёт без содержательного смысла.
Можете представлять себе несколько лампочек с числами, которые загораются в ~~дурдоме~~ с определёнными вероятностями :)

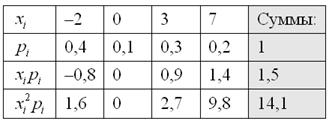
Решение: Основные вычисления удобно свести в таблицу. Сначала в верхние две строки записываем исходные данные. Затем рассчитываем произведения , затем и, наконец, суммы в правом столбце:

Собственно, почти всё готово. В третьей строке нарисовалось готовенькое математическое ожидание: .

Дисперсию вычислим по формуле:

И, наконец, среднее квадратическое отклонение:
– лично я обычно округляю до 2 знаков после запятой.

Все вычисления можно провести на калькуляторе, а ещё лучше – в Экселе:

вот здесь уже трудно ошибиться :)

Ответ:

Желающие могут ещё более упростить свою жизнь и воспользоваться моим калькулятором (демо), который не только моментально решит данную задачу, но и построит тематические графики (скоро дойдём). Программа доступна за символическую плaтy. Спасибо за поддержку проекта!

Пара заданий для самостоятельного решения:

Вычислить дисперсию случайной величины предыдущего примера по определению.

И аналогичный пример:

Дискретная случайная величина задана своим законом распределения:

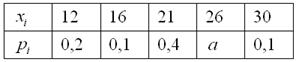
Да, значения случайной величины бывают достаточно большими (пример из реальной работы), и здесь по возможности используйте Эксель. Как, кстати, и в Примере 7 – это быстрее, надёжнее и приятнее.

Решения и ответы внизу страницы.

В заключение 2-й части урока разберём ещё одну типовую задачу, можно даже сказать, небольшой ребус:

Дискретная случайная величина может принимать только два значения: и , причём . Известна вероятность , математическое ожидание и дисперсия .

Решение: начнём с неизвестной вероятности. Так как случайная величина может принять только два значения, то сумма вероятностей соответствующих событий:

и поскольку , то .

Осталось найти …, легко сказать :) Но да ладно, понеслось. По определению математического ожидания:
– подставляем известные величины:

– и больше из этого уравнения ничего не выжать, разве что можно переписать его в привычном направлении:

ОК, едем дальше. По формуле вычисления дисперсии:
– подставляем известные данные:

О дальнейших действиях, думаю, вы догадываетесь. Составим и решим систему:

Десятичные дроби – это, конечно, полное безобразие; умножаем оба уравнения на 10:

Вот так-то лучше. Из 1-го уравнения выражаем:
(это более простой путь) – подставляем во 2-е уравнение:

Возводим в квадрат и проводим упрощения:

В результате получено квадратное уравнение, находим его дискриминант:
– отлично!

и у нас получается два решения:

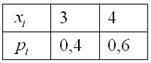
Условию удовлетворяет первая пара значений. С высокой вероятностью всё правильно, но, тем не менее, запишем закон распределения:

и выполним проверку, а именно, найдём матожидание:

В результате получены исходные значения, что и требовалось проверить.

Ответ:

Следует отметить, что это технически трудное задание, и поэтому в нём следует проявлять повышенное внимание. Потренируйтесь самостоятельно:

Случайная величина принимает только два значения: и , причём . Найти эти значения, если .

Тут вычисления попроще.

Жду вас в третьей, заключительной части урока, где мы познакомимся с многоугольником и функцией распределения. Её лучше изучить как можно скорее!

Решения и ответы:

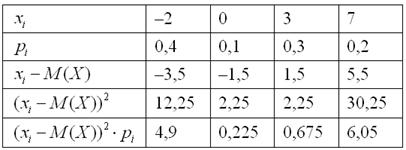
Пример 7. Решение: вычислим математическое ожидание:

Вычислим дисперсию по определению:
Заполним расчётную таблицу:

Таким образом:

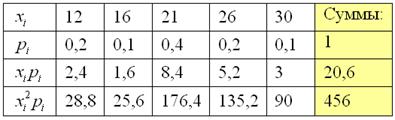
Пример 8. Решение: случайная величина может принять только 5 значений, поэтому:

Заполним расчётную таблицу:

Математическое ожидание: .
Дисперсию вычислим по формуле:

Среднее квадратическое отклонение:

Пример 10. Решение: т.к. случайная величина может принимать только 2 значения, то:
.
По определению математического ожидания:

По формуле вычисления дисперсии:

Составим и решим систему:

Умножим оба уравнения на 5:

Из первого уравнения выразим: – подставим во второе:

Решим полученное квадратное уравнение:

Условию удовлетворяет первая пара.

Автор: Емелин Александр

(Переход на главную страницу)

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

Читайте также: