Аксиомы геометрии 7 класс конспект
Обновлено: 06.07.2024
Цель: ввести понятие аксиомы, рассмотреть аксиому параллельных прямых и ее следствия.
I. Постановка цели урока
II. Проверка домашнего задания по вопросам
1. Дать определение параллельных прямых
2. Назвать все углы при пересечении двух прямых секущей
3.Сформулировать признаки параллельности двух прямых (1 - 3), рассмотреть их применение на примере такой задачи:
Дано: прямая с пересекает а и b, 1 = 30 о , 5 в 5 раз больше.
Решите задачу тремя способами: через накрест лежащие углы, через соответственные углы и через односторонние углы (устно, по вариантам).
4. Рассказать о практических способах построения параллельных прямых (по пункту 26 учебника).
Физкультминутка
Раз – потянуться
Два – нагнуться
Три – оглянуться
Четыре – присесть
Пять – руки вверх
Шесть – вперед
Семь – опустили
Восемь – сели
Девять – встали
Десять – снова сели
III. Изучение нового материала
Итак, исходя из вышеизложенного, мы можем решить такую задачу: через точку, не лежащую на прямой, провести прямую, параллельную данной. Возникает вопрос: а сколько таких прямых можно провести?
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
А как это доказать?
Может существует еще одна прямая b / , проходящая через т. М и параллельная прямой а?
Оказывается, доказать это невозможно, хотя ученые на протяжении многих веков пытались это сделать. Называли эту проблему проблемой пятого постулата, потому что в геометрии Евклида это утверждение называлось пятым постулатом, а Евклид жил в III веке до нашей эры.
И только наш русский ученый Н.И. Лобачевский, впоследствии ставший ректором Казанского университета, обосновал, что это утверждение не может быть доказано.
Значит это аксиома. Оказывается, кроме геометрии, которую изучают в школе, есть и другие геометрии, в которых нет параллельных прямых. Посмотрите на глобус, вот вам пример геометрии кривого пространства: меридианы пересекаются в двух точках, в северном и южном полюсах.
Послушайте об этом стихотворение.
Аксиома – это утверждение, которое принимается без доказательства. На самом деле, с аксиомами мы с вами уже встречались в I главе и во II главе.
Сколько прямых можно провести через 2 точки?
Через любые две точки можно провести прямую, и притом только одну. Это аксиома.
Сколько отрезков, равных данному, можно отложить на данном луче от его начала?
На любом луче от его начала можно отложить отрезок, равный данному, и притом только один. Это тоже аксиома.

Об аксиомах планиметрии вы можете прочитать в конце учебника в приложении 1.
Ребята читают по очереди аксиомы и рассматривают их геометрические интерпретации.


Так как же построена геометрия?
Вводятся основные понятия.
Затем принимаются без доказательства некоторые свойства – аксиомы.
На основании аксиом и ранее доказанных теорем доказываются следующие теоремы.
Пример: при доказательстве 2 и 3 признаков параллельности был использован 1 признак о накрест лежащих углах.
Цель последующих уроков – научиться использовать аксиому параллельных прямых при изучении свойств прямых и при решении задач.
У этой аксиомы есть следствия 1 о и 2 о .
Утверждения, которые выводятся непосредственно из аксиом или теорем, называются следствиями.
1 о . Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
2 о . Если две прямые параллельны третьей прямой, то они параллельны.
Следствия 1 о и 2 о доказываются с помощью аксиомы параллельных прямых. Изучите их доказательства самостоятельно по учебнику: 1-ый вариант - 1 о , а 2-ой вариант - 2 о .
Ребята рассказывают доказательства у доски.
В этих следствиях используется метод доказательства, называемый методом от противного, частично мы его уже использовали, например, при изучении свойства: если две прямые перпендикулярны третьей, то они не пересекаются.
IV. Задание на дом
V. Итоги урока
Какое утверждение называется аксиомой?
Сформулируйте аксиому параллельных прямых и следствия из нее.
В заключении посмотрите сценку о том, как построена геометрия.
Разговорились как-то аксиомы, теоремы, доказательства и задачи.
– Мы, аксиомы, основа всей геометрии! Без нас бы и геометрии не было! – горделиво заговорили аксиомы. Если человек попадет на необитаемый остров без учебника геометрии и с ним будем все мы, то он, опираясь на нас, создаст всю остальную геометрию. Значит, мы основа основ!
- Хороша бы была геометрия, если бы не было нас, теорем! – возразили мощным хором теоремы. – Любой школьник с грустью улыбнется, представив, что это за геометрия была бы без нас! Ничего, кроме аксиом. Мы, теоремы, царствуем по всему учебнику геометрии!
– Не ссорьтесь, - заговорило с достоинством доказательство.
– Без меня и аксиомы ни к чему. Зачем они тогда? Без меня и вы, теоремы, не появились бы на свет. Но и меня без вас бы не было. Разве можно считать доказательством рассуждения, которые опираются не на аксиомы и теоремы, а на то, что кому-то придет в голову.
– Вы забыли о нас, задачах! – прошумели мощной океанской волной задачи. – Ведь через нас только ученики и начинают вас по-настоящему понимать и ценить. Из-за задач – и в вас нужда, а то бы вас и забыли.
– Все вы правы, дети мои! – прозвучал могучий голос, которым словно говорили тысячелетия и современность. – У каждого из вас свои достоинства и заслуги. Вы о них и говорите. Но существуют они только тогда, когда вы все вместе. Коль не будет в вас единства, не будет и достоинств ваших. Исчезнет один из вас - погибнут все остальные. И я, Геометрия, погибну. Так держитесь вместе, будьте дружны и едины, помогайте друг другу – и ваша мать Геометрия будет жить вечно. Да расскажите об этом тем, кто меня изучает! Если они умны, они все поймут. Все сказанное мной и вами важно прежде всего для изучающих, любящих или желающих познать меня.
1. Атанасян Л.С. и др. Геометрия, 7-9, - М.: Просвещение, 2003. – 384с.
Аксиома – это утверждение, которое принимается в качестве исходного, без доказательства в рамках данной теории.
Аксиома параллельных прямых.
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Следствия из аксиомы.
Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
Если две прямые, параллельны третьей прямой, то они параллельны.
Основная литература:
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Дополнительная литература:
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения
Построение геометрии
Геометрия на плоскости изучает фигуры: сначала даются их определения, затем доказываются свойства или отношения в виде теорем.
Однако есть утверждения, которые принимаются в качестве исходных, они не доказываются. Это аксиомы.
Аксиома параллельных прямых.
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Следствия из аксиомы.
Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
Если две прямые параллельны третьей прямой, то они параллельны.
Приведём примеры аксиом, которые уже встречали в предыдущих параграфах, хотя они не назывались аксиомами.
- Через любые две точки проходит прямая, и притом только одна.
- На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.
- От любого луча можно отложить угол, равный данному неразвёрнутому углу, и притом только один.
Евклид является автором аксиоматического подхода к построению геометрии.

Аксиома параллельных прямых:
через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
На рисунке через точку М проведены две прямые. Но только одна из них прямая b параллельна прямой а.

Утверждения, которые выводятся из аксиом или теорем, называются следствиями, и они доказываются.
Следствия из аксиомы параллельных прямых.
1. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
Доказательство методом от противного.
Пусть a ║b, c пересекает прямую a в точке M. Предположим, что прямая c не пересекает b. Тогда через точку M проходит две прямые a и c параллельные b. Это противоречит аксиоме, значит предположение неверно, т. е. прямая c пересекает b.

2. Если две прямые параллельны третьей прямой, то они параллельны.
Доказательство методом от противного.
Пусть a ║ c, b ║ c.
Предположим, что прямые a и b не параллельны, т. е. пересекаются в точке M. Тогда через точку M проходит две прямые a и b параллельные c. Это противоречит аксиоме, значит, предположение неверно, т. е. прямая a параллельна прямой b.

Разбор заданий тренировочного модуля
№ 1. Доказать существование прямой, параллельной данной.

- Проведём через точку М прямую c ┴ а.
- Затем проведём прямую b ┴ c.
- Так как прямые a и b перпендикулярны прямой c, то они параллельны.
№ 2. Через точку А, не лежащую на прямой р, проведены четыре различные прямые.
Сколько из них пересекает прямую р?

1 случай. Если одна из прямых параллельна р. Тогда три других пересекают прямую р, согласно следствию 1 из аксиомы параллельных прямых.
2 случай. Если ни одна из прямых не параллельна р. Тогда все четыре пересекают прямую р.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности



Конспект урока "Аксиома параллельных прямых"
На предыдущих уроках мы рассмотрели ряд теорем, доказательства которых опираются на уже доказанные ранее теоремы. В таком случае возникает вопрос: А на чём основаны доказательства самых первых теорем? Ответ такой: Доказательства самых первых теорем основаны на аксиомах.
Аксиомы возникли из опыта, они являются наглядно очевидными и не вызывают сомнений.
Нам уже известны некоторые аксиомы. Например:
1. Через любые две точки проходит прямая и притом только одна.

2. На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.

3. От любого луча в заданную сторону можно отложить угол, равный данному неразвёрнутому углу, и притом только один.

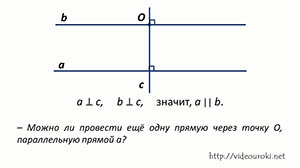
Пусть дана прямая а и не лежащая на ней произвольная точка О. Докажем, что через точку О можно провести прямую, параллельную прямой а.

Проведём две прямые: сначала прямую c, перпендикулярно к прямой а, а затем прямую b, перпендикулярно к прямой c.

Получили, что прямые а и b перпендикулярны к прямой c, а значит, они параллельны.
А теперь возникает вопрос: можно ли провести ещё одну прямую через точку О, параллельную прямой а? Ответ на этот вопрос не является очевидным. Оказывается, что утверждение о единственности прямой, проходящей через данную точку и параллельной прямой, не может быть доказано на основании остальных аксиом и само является аксиомой.
Аксиома параллельных прямых:
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Следствия из аксиомы:
1. Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.

2. Если две прямые параллельны третьей, то они параллельны.

Дан треугольник АВС. Сколько прямых, параллельных стороне АС можно провести через вершину В?

Так как по аксиоме параллельных прямых через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной:

То есть через точку В можно провести единственную прямую, параллельную стороне АС треугольника АВС.
И он предположил, что через точку, не лежащую на данной прямой, проходит более чем одна прямая, параллельная данной. В результате получилась новая система определений и теорем. Эту геометрию назвали геометрией Лобачевского.
Как оказалось, геометрия Лобачевского точнее описывает геометрию Вселенной, чем геометрия Евклида. Результатами геометрии Лобачевского пользовался учёный Альберт Энштейн.
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
Тема: Аксиома параллельных прямых
Цели: Дать представление об аксиомах геометрии; ввести аксиому параллельных прямых и следствия из нее.
Тип урока: Комбинированный.
Задачи урока:
Образовательная: Начать формирование у обучающихся представления об аксиоме параллельных прямых и следствий из нее.
Воспитательная: Воспитать у обучающихся интерес к предмету через исторические справки.
Развивающая: Развитие у обучающихся умения сравнивать через проведение изучение новой темы.
Средства урока: мел, доска, готовые чертежи, проектор и диск к учебнику.
1. Проверка домашнего задания.
Пройти посмотреть выполнение работы.
2. Актуализация опорных знаний.
- Что мы изучали на прошлом уроке?
- Какие прямые называются параллельными?
- Какие признаки параллельных прямых вы знаете? Сформулируйте их.
3. Изучение нового материала.
Изучение материала из пункта 27 учебника и из Приложения 1 на с. 344-348 учебника, Приложение 2 на с. 349-351.
Записать в тетрадях: Аксиомами называются те основные положения геометрии, которые принимаются в качестве исходных положений, на основе которых доказываются далее теоремы и строится вся геометрия.
Предложить учащимся задачу, решение которой дано в начале п. 28: через точку А, не лежащую на прямой а, провести прямую, параллельную прямой а. Решение этой задачи доказывает существование прямой, проходящей через данную точку и параллельной данной прямой.
1. Провести через точку А прямую b так, что а┴ b .
2. Провести через точку А прямую с так, что b ┴с.
Доказательство: 0 , т.е. накрест лежащие углы равны при прямых а и с секущей b , следовательно а‖с.
- Всегда ли можно провести такую прямую?
- Сколько таких прямых можно провести?
- Чем отличается вышеуказанное утверждение от аксиомы параллельных прямых? ( в аксиоме говорится о единственности такой прямой)
4.Закрепление изученного материала.
Устно решить задачу №197.
Полезно на рисунке показать учащимся два возможных случая расположения прямых:
1) все четыре прямые пересекают прямую р;
2) одна из четырех прямых параллельна прямой р, а три другие прямые пересекают ее.
Эти два случая иллюстрируют ответ на вопрос задачи: по крайней мере, три прямые пересекают прямую р.
Записать в тетрадях: следствиями называются утверждения, которые выводятся непосредственно из аксиом или теорем.
Рассмотреть следствия 1° и 2° из аксиомы параллельных прямых.
Прямая А D пересекает прямые АВ, АЕ и АС в точке А и прямые ВС и Р Q .
А D ׀׀ р, значит р пересекает прямые АВ, АЕ, АС, ВС и Р Q по следствию: если прямая пересекает одну из параллельных прямых, то она пересекает и другую.
5. Формирование умений и навыков.
Решение задачи № 218:
Отметим произвольную точку, не лежащую на прямой b , и проведем через нее прямую с, параллельную прямой b . Так как прямая а пересекает прямую b , то она пересекает и прямую с. Таким образом, прямая с пересекает прямую а и параллельна прямой b .
Решение задачи № 219*.
Предположим противное, что прямые а и b не параллельны, то есть пересекаются. Тогда можно провести прямую с, которая пересекает прямую а и не пересекает прямую b (из решения задачи № 218). Но это противоречит условию задачи. Значит, наше предположение неверно и а || b .
7. Итоги урока.
- Что нового вы сегодня узнали?
- С какими понятиями познакомились?
- Сформулируйте определение аксиомы, следствия.
- Сколько следствий из аксиомы параллельных прямых вы знаете? Сформулируйте их.
Читайте также:

