Точка перегиба определение кратко
Обновлено: 02.07.2024
Направление выпуклости кривой является важной характеристикой ее формы.
Понятие о выпуклости, вогнутости и точках перегиба функции дадим, исходя из рис. 6. На этом рисунке изображен график функции, выпуклой на интервале , вогнутой на интервале , и y которой точка x0, разделяющая интервалы выпуклости и вогнутости, есть точка перегиба функции . Кстати, точка M0 называется точкой перегиба графика функции (не путать точку перегиба функции x0 и точку перегиба её графика M0). Интервалы выпуклости, вогнутости и точки перегиба функции – важные характеристики любой функции, поэтому полезно уметь их находить.
Рассмотрим подробнее функцию на ее интервале выпуклости (рис. 7 (а)) и на ее интервале вогнутости (рис. 7 (б)).
Для выпуклой функции (рис. 7 (а)) касательная к ее графику в любой его точке расположена выше графика, причем с увеличением абсциссы x точки касания эта касательная поворачивается по часовой стрелке. Это значит, что с увеличением x угол наклона касательной к оси ох уменьшается. Но тогда уменьшается и угловой коэффициент касательной . А значит, с увеличением x уменьшается (убывает) равная ему производная функции . Но если некая функция убывает, то, как мы знаем, ее производная отрицательна. Значит, на всем интервале выпуклости функции .
Аналогичное рассуждение приводит к выводу, что если функция вогнута на некотором интервале (см. рис. 7 (б)), то для любого x из этого интервала (проведите это рассуждение самостоятельно).
Верно, естественно, и обратное: если на некотором интервале оси ох вторая производная функции положительна, то функция вогнута на этом интервале. А если эта производная отрицательна – то функция выпукла на указанном интервале.
Определение 3. Кривая обращена выпуклостью вверх на интервале , если все точки кривой лежат ниже любой ее касательной на этом интервале.
Определение 4. Кривая обращена выпуклостью вниз на интервале , если все точки кривой лежат выше любой ее касательной на этом интервале.
Кривая, обращенная выпуклостью вверх, будет называть выпуклой, а обращенную выпуклостью вниз – вогнутой.
Теорема 5:Если во всех точках интервала вторая производная f(x) отрицательна, т.е. , то кривая y=f(x) на этом интервале обращена выпуклостью вверх ( кривая выпукла )
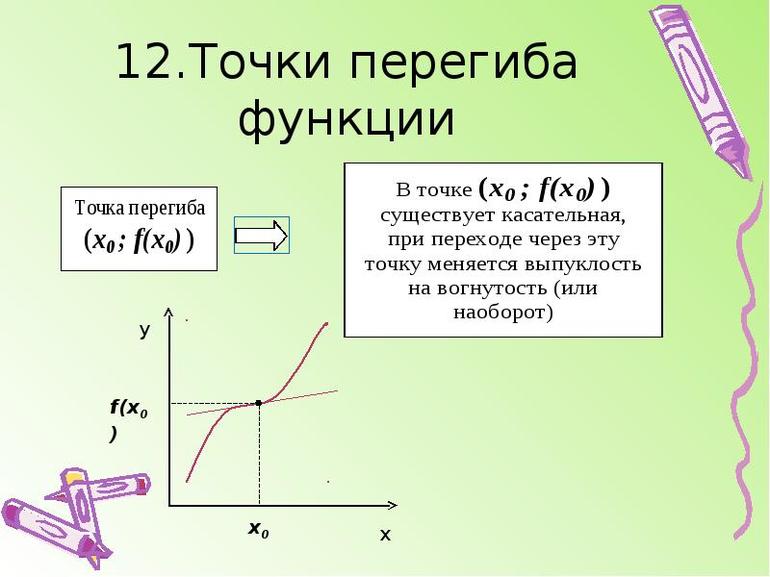
Доказательство. Возьмем в интервале произвольную точку х=х0 и проведем касательную к кривой в точке с абсциссой х=х0.Теорема будет доказана, если мы установим, что все точки кривой на интервале лежат ниже этой касательной, т.е. что ордината любой точки кривой y=f(x) меньше ординаты y касательной при одном и том же значении х.
Уравнение кривой имеет вид
Уравнение касательной к кривой в точке х=х0 имеет вид
Откуда следует, что разность ординат кривой и касательной при одном и том же значении х равна
Применяя теорему Лагранжа к разности , получим:
( где с лежит между х0 и х ). К выражению, стоящему в квадратных скобках, снова применим теорему Лагранжа, тогда
( где с1 лежит между х0 и с ).
Рассмотрим два случая:

1) Пусть х>x0. Тогда x0
Теорема 7.Пусть кривая определяется уравнениемy=f(x). Если или не существует и при переходе через значение x=a производная меняет знак, то точка кривой с абсциссой x=a есть точка перегиба.
Из всего сказанного вытекает
схема исследования функции на выпуклость-вогнутость
и точки перегиба:
1. Находим область определения функции, а заодно устанавливаем интервалы ее непрерывности и точки разрыва (стандартное начало любого исследования функции).
2. Находим вторую производную .
3. Находим точки (значения x), подозрительные на перегиб. То есть находим те точки (значения x), в которых вторая производная функции или равна нулю, или не существует:
б) не существует
4. Наносим все найденные подозрительные на перегиб точки на область определения функции (на ось ох) и отмечаем (например, дугами) интервалы, на которые разобьется этими дугами область определения функции. В каждом из этих интервалов выясняем знак второй производной . По установленным знакам этой производной отмечаем интервалы выпуклости и вогнутости функции ((–) – выпуклость, (+) – вогнутость), а также точки перегиба функции.
5. Вычисляем значения функции во всех найденных точках ее перегиба и находим тем самым точки перегиба графика функции.
Пример 4. Исследовать на выпуклость-вогнутость и точки перегиба функцию (в примере 2 она уже исследовалась на возрастание-убывание и точки экстремума).
Решение. Реализуем изложенную выше схему.
1. Функция определена, а следовательно и непрерывна для любых x от до .
3. Найдем точки (значения x), подозрительные на перегиб:
б) не существует Þ таких x нет.
4. Нанесем на ось ох найденную подозрительную на перегиб точку . Ось ох (область определения функции) разобьется этой точкой на два интервала:
Определяем знаки второй производной в этих интервалах (они отмечены на рис. выше). Тем самым устанавливаем интервалы выпуклости (знак ) и вогнутости (знак ) , а также устанавливаем, что – точка перегиба функции.
5. Вычисляем значение функции в точке ее перегиба и тем самым определим точку перегиба графика функции (она указана на рис. 4).
Направление выпуклости кривой является важной характеристикой ее формы.
Понятие о выпуклости, вогнутости и точках перегиба функции дадим, исходя из рис. 6. На этом рисунке изображен график функции, выпуклой на интервале , вогнутой на интервале , и y которой точка x0, разделяющая интервалы выпуклости и вогнутости, есть точка перегиба функции . Кстати, точка M0 называется точкой перегиба графика функции (не путать точку перегиба функции x0 и точку перегиба её графика M0). Интервалы выпуклости, вогнутости и точки перегиба функции – важные характеристики любой функции, поэтому полезно уметь их находить.
Рассмотрим подробнее функцию на ее интервале выпуклости (рис. 7 (а)) и на ее интервале вогнутости (рис. 7 (б)).
Для выпуклой функции (рис. 7 (а)) касательная к ее графику в любой его точке расположена выше графика, причем с увеличением абсциссы x точки касания эта касательная поворачивается по часовой стрелке. Это значит, что с увеличением x угол наклона касательной к оси ох уменьшается. Но тогда уменьшается и угловой коэффициент касательной . А значит, с увеличением x уменьшается (убывает) равная ему производная функции . Но если некая функция убывает, то, как мы знаем, ее производная отрицательна. Значит, на всем интервале выпуклости функции .
Аналогичное рассуждение приводит к выводу, что если функция вогнута на некотором интервале (см. рис. 7 (б)), то для любого x из этого интервала (проведите это рассуждение самостоятельно).
Верно, естественно, и обратное: если на некотором интервале оси ох вторая производная функции положительна, то функция вогнута на этом интервале. А если эта производная отрицательна – то функция выпукла на указанном интервале.
Определение 3. Кривая обращена выпуклостью вверх на интервале , если все точки кривой лежат ниже любой ее касательной на этом интервале.
Определение 4. Кривая обращена выпуклостью вниз на интервале , если все точки кривой лежат выше любой ее касательной на этом интервале.
Кривая, обращенная выпуклостью вверх, будет называть выпуклой, а обращенную выпуклостью вниз – вогнутой.
Теорема 5:Если во всех точках интервала вторая производная f(x) отрицательна, т.е. , то кривая y=f(x) на этом интервале обращена выпуклостью вверх ( кривая выпукла )
Доказательство. Возьмем в интервале произвольную точку х=х0 и проведем касательную к кривой в точке с абсциссой х=х0.Теорема будет доказана, если мы установим, что все точки кривой на интервале лежат ниже этой касательной, т.е. что ордината любой точки кривой y=f(x) меньше ординаты y касательной при одном и том же значении х.
Уравнение кривой имеет вид
Уравнение касательной к кривой в точке х=х0 имеет вид
Откуда следует, что разность ординат кривой и касательной при одном и том же значении х равна
Применяя теорему Лагранжа к разности , получим:
( где с лежит между х0 и х ). К выражению, стоящему в квадратных скобках, снова применим теорему Лагранжа, тогда
( где с1 лежит между х0 и с ).
Точкой перегиба функции называется точка, в которой эта функция меняет направление выпуклости.
Геометрический смысл точки перегиба функции
В точке перегиба график функции переходит с одной стороны касательной на другую.
Необходимое условие существования точки перегиба функции. Для того чтобы функция имела перегиб в точке ,\; f\left(x_\right)\right)" width="117" height="18" />
, необходимо, чтобы либо вторая производная этой функции обращалась в нуль в точке " width="18" height="11" />
, либо чтобы " width="18" height="11" />
была для второй производной точкой разрыва, либо чтобы вторая производная в точке " width="18" height="11" />
не существовала.
Первое достаточное условие существования точки перегиба функции. Пусть функция имеет вторую производную в некоторой выколотой -окрестности точки " width="18" height="11" />
и дифференцируема в этой точке. Если при переходе через точку " width="18" height="11" />
вторая производная функции меняет знак, то точка ,\; f\left(x_ \right)\right)" width="117" height="18" />
является точкой перегиба функции .
![]()
вторая производная равна нулю, а третья нет
![]()
является точкой перегиба функции .
Примеры решения задач
| Задание | Найти точки перегиба функции |
| Решение | Найдем вторую производную заданной функции. По определению , следовательно, найдем сначала первую производную |
![]()
Приравниваем к нулю вторую производную и находим корни полученного уравнения
![]()
Найдем третью производную заданной функции и проверим её значение в найденных точках
![]()
![]()
Следовательно, в точках =-1;\ x_ =1" width="134" height="16" />
функция -6x^ +4" width="137" height="20" />
имеет перегиб. Найдем значение функции в этих точках:
![]()
| Задание | Найти точки перегиба функции |
| Решение | Найдем вторую производную заданной функции |
![]()
Приравняем её к нулю и найдем корни полученного уравнения
![]()
В промежутках функция принимает положительные значения, следовательно , а в промежутках . Значит, в точках вторая производная меняет знак и в этих точках график функции имеет перегиб.

Общие сведения
Для определения точек перегиба функции необходимо разобрать основные определения и базовые компоненты, необходимые для их нахождения. Функция — математическая запись зависимости одной переменной от другой. Последняя называется аргументом, а на графике в декартовой системе координат ее определяет абсцисса.
Графиком или графическим представлением называется геометрическое тело, находящееся в системе координат и состоящее из определенного количества точек с заданными координатами. Перегиб — совокупность координат по ординате и абсциссе, в которой наблюдается изменение поведения функции, образующих выпуклость или вогнутость.
Для нахождения последних следует иметь определенные базовые навыки определения производных первого, второго и третьего порядков.
Понятие производной
Производная — операция, используемая не только при исследовании функции, но и при описании какого-либо процесса, определения площади геометрических тел и т. д. Она позволяет существенно сократить время, необходимое для вычислений. Главным условием ее определения является постоянный рост функции. Если последняя не растет (остается постоянной — константой), ее дифференциал равен нулю. В этом случае говорят, что она не существует.
Однако производная применяется не только в алгебре, но и в других сферах деятельности человека. С ее помощью можно вычислить силу, мощность, величину тока и другие физические величины, зависящие от определенных параметров.

В медицине производная применяется при исследовании лекарственных препаратов, обладающих побочными действиями. Последние отрицательно влияют на жизнедеятельность организма человека. Следовательно, ученые в области фармацевтики добиваются лучшего лечебного эффекта с минимальной вероятностью пагубного воздействия на организм.
Производная применяется при проектировании компьютерных игр, в которых персонажи осуществляют сложные движения.
Траектории последних нужно рассчитать скоростными методами, а их и предоставляют дифференциалы функций движения различных компонентов системы, т. е. прыжки героя и противников, движение элементов внешней среды (деревьев, травы и т. д. ).
Смысловые интерпретации
Для понимания физического и математического смысла производной нужно разобрать ее определение в математической интерпретации: производная представляет границу предела отношения приращения некоторой функциональной зависимости двух или более переменных к приращению независимой переменной (аргумента), который стремится к нулевой величине.
Из определения можно сделать вывод, что обязательное условие существование дифференциала — постоянный рост или убывание функции в заданной точке. Обратной операцией дифференцирования является интегрирование или поиск первообразной.
Геометрическим смыслом является величина тангенса угла наклона прямой-касательной к графическому отображению. Для построения необходимо провести прямую, которая должна пересекать график функции минимум в двух точках, а затем рассмотреть место пересечения. Это будет ось вращения прямой. Если и далее вращать секущую, она в некотором положении будет касаться графика функции в одной точке, т. е. преобразуется в касательную.
Физический смысл основан на характеристике изменения скорости роста физической величины. Например, при рассмотрении закона движения тела в пространстве S= s (t). Путь, пройденный им, зависит от времени и скорости. Для нахождения последней V (tм) в текущий момент времени tм необходимо вычислить производную, т. е. V (tм)=[s (tм)]'.
При вычислении производной второго порядка величина будет называться ускорением, т. е. a (tм)=[[s (tм)]']'=[V (tм)]'. Для выполнения операции дифференцирования необходимо знать основные правила.
Правила дифференцирования
Для нахождения производных простых и сложных функций существуют определенные правила. К ним относятся:

- Постоянную величину (const) можно вынести за знак производной, т. е. (const*p (t))'=const*(p (t))'
- Дифференциал суммы (разности) двух и более тождеств эквивалентен производной каждой из компонентов, т. е. (p (t)+r (t)+s (t))'=p'(t)+r'(t)+s'(t) или (p (t)-r (t)-s (t))'=p'(t)-r'(t)-s'(t).
- Производная произведения двух простых выражений соответствует сумме дифференциала первой функции, умноженной на вторую, и l компонента, который умножается на дифференциал второго тождества. Математическая запись: (p (t)*r (t))'=p'(t)*r (t)+p (t)*r'(t).
- Если взять производную тождества частного двух функций, в числителе обыкновенной дроби следует записать разность произведений, состоящих из дифференциала I компонента и II, и дифференциала второго и первого, а затем результат разделить на квадрат второго выражения. Короткая математическая формулировка имеет вид: (p (t)/r (t))'=[p'(t)*r (t)-p (t)*r'(t)]/[r (t)]^2.
- Дифференциал сложного тождества состоит из произведения производных элементов, которые входят в его состав, т. е. [р (r (t))]'=[r (t)]' * [p (r (t))]'.
Для понимания последнего пункта необходимо разобрать пример p=(3/2)*sin (4t 2 −5). Для вычисления производной следует воспользоваться специальным алгоритмом, первым и последним правилами:
- Записать выражение с учетом знака дифференциала: p'=[(3/2)*sin (4t 2 −5)]'.
- Постоянную величину вынести за знак дифференциала (1 правило): p'=(3/2)*[sin (4t 2 −5)]'.
- Взять производную I элемента: [4t 2 −5]'=8t-0=8t.
- II: [sin (4t 2 −5)]'=cos (4t 2 −5).
- Записать результат: p'=8tcos (4t 2 −5).
Методика нахождения
Нахождение производной заданной функции строится на правилах. Методика имеет следующий вид:

- Написать выражение.
- Произвести математические операции по упрощению тождества, чтобы удобно было находить дифференциал.
- Выполнить операцию нахождения производной.
- Записать ответ.
Однако при нахождении точек перегиба необходимо уметь вычислять дифференциалы второго и третьего порядка. Это делать несложно, поскольку достаточно взять один раз производную (l порядка), а затем — второй (II), а также III.
Все правила действуют для дифференциалов любого порядка. Кроме того, очень важно после операции дифференцирования приводить подобные компоненты, т. к. это действие позволит осуществить вычисления за короткий промежуток времени, а также избежать множества ошибок.
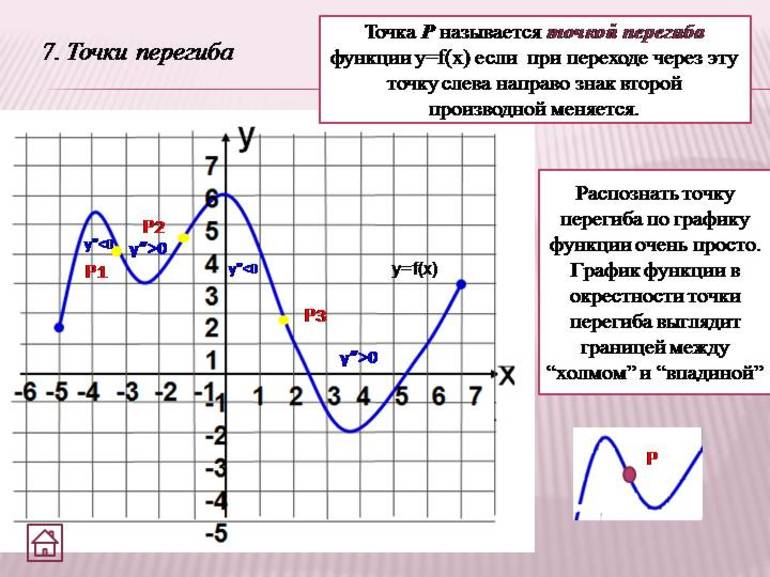
- Написать выражение, учитывая знак производной: s'(t, v)=[4t*8v+2t 2 +3v 3 ]'.
- Найти производную произведения: [4t*8v]'=32v+32t.
- Дифференциал суммы: [2t 2 +3v 3 ]'=t+v.
- Привести подобные слагаемые: 32v+32t+t+v=33t+33v.
- Вынести 33 за скобки и взять вторую производную: 33[t+v]'=66.
- Результат: s'(t, v)=66.
Cледует обратить внимание на четвертый пункт алгоритма, в котором нужно приводить подобные элементы, поскольку в пятом пункте дифференциал найти довольно просто.
Для проверки результата можно воспользоваться специальным приложением, которое называется онлайн-калькулятором. Однако на начальных стадиях обучения специалисты не рекомендуют пользоваться им для решения задач.
Выпуклости и вогнутости
Для нахождения точек перегиба на заданном интервале необходимо знать основное условие их существования.
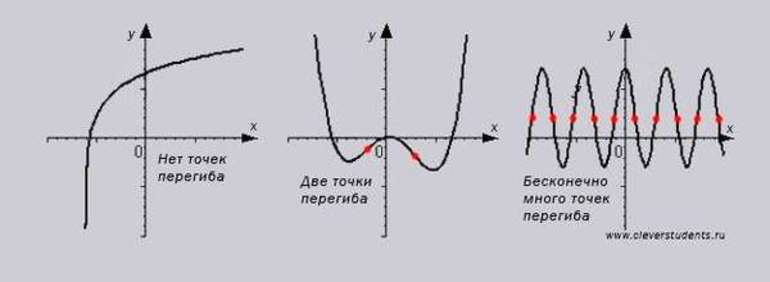
Оно гласит: функция s (t) имеет выпуклость или вогнутость в некоторой точке P (to, s (t)), когда производная II порядка обращается в нулевую величину, отсутствует или является разрывом. Кроме того, существуют 2 достаточных условия существования искомых точек:
- ll производная меняет знак и направление, но по модулю эквивалентна искомой функции.
- В заданной точке дифференциал ll порядка эквивалентен нулю, а третьего — нет.
Пример решения
Задача решается по следующему алгоритму:
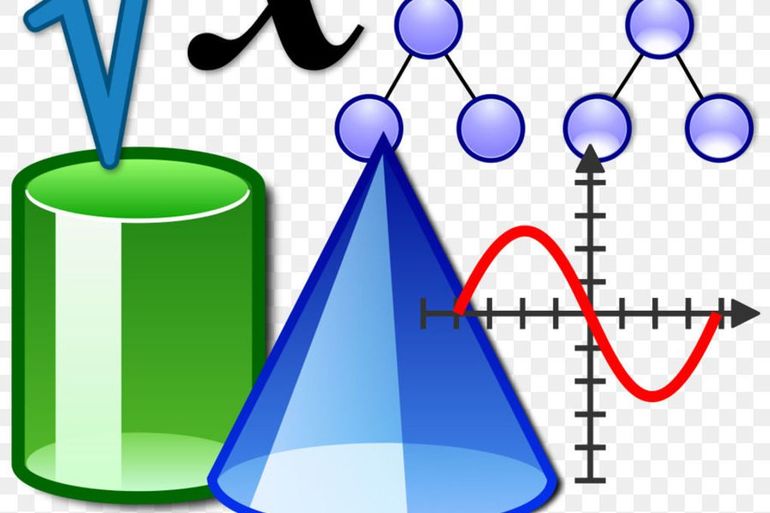
Следует обратить внимание на 6 пункт алгоритма. В нем значения не равны нулю. Из этого следует, что у этого графика функции всего 2 точки перегиба, координаты которых эквивалентны (0;-2) и (2/3;2).
Таким образом, для нахождения точек перегиба функции для начала следует ознакомиться с производной и правилами ее нахождения, а затем переходить к условиям поиска вогнутостей и выпуклостей.
Локомотив исследования функции методами дифференциального исчисления неумолимо приближает нас к конечной станции, и после изучения непрерывности, области определения, интервалов знакопостоянства, асимптот, интервалов монотонности и экстремумов функции осталось рассмотреть выпуклость, вогнутость и перегибы графика. Начнём с так полюбившихся посетителям сайта физических упражнений. Пожалуйста, встаньте и наклонитесь вперёд либо назад. Это выпуклость. Теперь вытяните руки перед собой ладонями вверх и представьте, что держите на груди большое бревно… …ну, если не нравится бревно, пусть будет ещё что/кто-нибудь =) Это вогнутость. В ряде источников встречаются синонимичные термины выпуклость вверх и выпуклость вниз, но я сторонник коротких названий.
Назовём хордой отрезок, соединяющий две различные точки графика.
График функции является выпуклым на некотором интервале, если он расположен не ниже любой хорды данного интервала. Подопытная линия выпукла на , и, очевидно, что здесь любая часть графика расположена НАД своей хордой. Иллюстрируя определение, я провёл три чёрных отрезка.
График функции являются вогнутым на интервале, если он расположен не выше любой хорды этого интервала. В рассматриваемом примере пациент вогнут на промежутке . Пара коричневых отрезков убедительно демонстрирует, что тут и любой кусок графика расположен ПОД своей хордой.
Второй подход к определению выпуклости/вогнутости в теории даётся через касательные:
Выпуклый на интервале график расположен не выше касательной, проведённой к нему в произвольной точке данного интервала. Вогнутый же на интервале график – не ниже любой касательной на этом интервале.
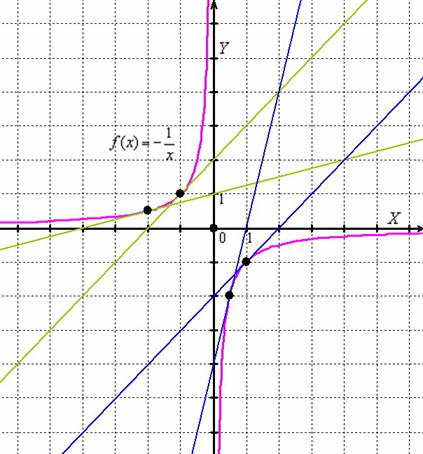
Гипербола вогнута на интервале и выпукла на :
При переходе через начало координат вогнутость меняется на выпуклость, однако точку НЕ СЧИТАЮТ точкой перегиба, так как функция не определена в ней.
Более строгие утверждения и теоремы по теме можно найти в учебнике, а мы переходим к насыщенной практической части:
Как найти интервалы выпуклости, интервалы вогнутости
и точки перегиба графика?
Материал прост, трафаретен и структурно повторяет исследование функции на экстремум.
Выпуклость/вогнутость графика характеризует вторая производная функции.
Пусть функция дважды дифференцируема на некотором интервале. Тогда:
– если вторая производная на интервале, то график функции является выпуклым на данном интервале;
– если вторая производная на интервале, то график функции является вогнутым на данном интервале.
Необходимое условие перегиба
Если в точке есть перегиб графика функции , то:
либо значения не существует (разберём, читайте!).
Данная фраза подразумевает, что функция непрерывна в точке и в случае – дважды дифференцируема в некоторой её окрестности.
Необходимость условия говорит о том, что обратное справедливо не всегда. То есть из равенства (либо небытия значения ) ещё не следует существования перегиба графика функции в точке . Но и в той, и в другой ситуации называют критической точкой второй производной.
Достаточное условие перегиба
Если вторая производная при переходе через точку меняет знак, то в данной точке существует перегиб графика функции .
Точек перегиба (встретился уже пример) может не быть вовсе, и в этом смысле показательны некоторые элементарные образцы. Проанализируем вторую производную функции :
Экспоненциальная функция также вогнута на :
Точек перегиба у графика , разумеется, нет.
Исследуем на выпуклость/вогнутость график логарифмической функции :
Таким образом, ветка логарифма является выпуклой на интервале . Вторая производная определена и на промежутке , но рассматривать его НЕЛЬЗЯ, поскольку данный интервал не входит в область определения функции . Требование очевидно – коль скоро там нет графика логарифма, то ни о какой выпуклости/вогнутости/перегибах речи, естественно, не заходит.
Как видите, всё действительно очень напоминает историю с возрастанием, убыванием и экстремумами функции. Похож и сам алгоритм исследования графика функции на выпуклость, вогнутость и наличие перегибов:
1) На первом шаге находим область определения функции и точки разрыва.
2) Разыскиваем критические значения. Для этого берём вторую производную и решаем уравнение . Точки, в которых не существует 2-й производной, но которые входят в область определения самой функции – тоже считаются критическими!
3) Отмечаем на числовой прямой все найденные точки разрыва и критические точки (ни тех, ни других может не оказаться – тогда чертить ничего не надо (как и в слишком простом случае), достаточно ограничиться письменным комментарием). Методом интервалов определяем знаки на полученных интервалах. Как только что пояснялось, рассматривать следует только те промежутки, которые входят в область определения функции . Делаем выводы о выпуклости/вогнутости и точках перегиба графика функции . Даём ответ.
Попытайтесь устно применить алгоритм для функций . Во втором случае, кстати, пример, когда в критической точке не существует перегиба графика. Впрочем, начнём с ненамного более сложных заданий:
Найти интервалы выпуклости, вогнутости и точки перегиба графика
Решение:
1) Функция определена и непрерывна на всей числовой прямой. Очень хорошо.
2) Найдём вторую производную. Можно предварительно выполнить возведение в куб, но значительно выгоднее использовать правило дифференцирование сложной функции:
Заметьте, что , а значит, функция является неубывающей. Хоть это и не относится к заданию, но на такие факты всегда желательно обращать внимание.
Найдём критические точки второй производной:
3) Проверим выполнение достаточного условия перегиба. Определим знаки второй производной на полученных интервалах .
Внимание! Сейчас работаем со второй производной (а не с функцией!)
Используем метод интервалов. Повторим его ещё разок.
Выберем наиболее выгодную точку интервала и вычислим в ней значение второй производной:
, следовательно, в любой точке интервала .
Из интервала возьмём значение и проведём аналогичное действие:
, а значит, и на всём интервале .

В результате получены следующие знаки второй производной:
Таким образом, график САМОЙ ФУНКЦИИ является выпуклым на интервале и вогнутым на . При переходе через вторая производная меняет знак, поэтому в данной точке существует перегиб графика.
Ответ: график функции выпукл на интервале и вогнут на , в точке существует перегиб графика.
Найти интервалы выпуклости, вогнутости и точки перегиба графика
Это пример для самостоятельного решения. Примерный образец оформления задания в конце урока. А чертежи – в начале =)
Рассмотрим более интересных представителей мира функций:
Найти интервалы выпуклости, вогнутости и точки перегиба графика
Решение:
1) Функция определена и непрерывна на .
2) Найдём критические точки второй производной:
Так как , то корни могут появиться только из решения квадратного уравнения:
Дискриминант положителен, и на подходе две критические точки:
Как и в ситуации с экстремумами функции, критические точки рациональнее не нумеровать подстрочными индексами. Ну а то, что они получились с радикалами – обычное дело.

3) Определим знаки второй производной. Можно использовать стандартный метод интервалов, но здесь , и учитывая, что – парабола, ветви которой направлены вверх, получаем:
Таким образом, график функции является выпуклым на интервале и вогнутым на . В обеих критических точках существуют перегибы графика (так как 2-я производная при переходе через них меняет знак).
Найдём ординаты данных точек:
(в целях вычислений подставлять, конечно, удобнее приближенные значения)
Ответ: график функции выпуклый на интервале и вогнутый на . В точках существуют перегибы графика.
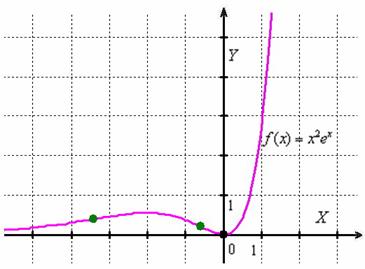
Чтобы закомментировать некоторые важные моменты нарисую его полностью:
Прежде всего, ещё раз подчёркиваю необходимость аккуратно выполнять чертежи: слева график вогнут. Кстати, обратите внимание, что там он не может быть выпуклым, поскольку линия бесконечно близко приближается к своей горизонтальной асимптоте. Когда аналитически получается подобный противоречивый результат, приходится перепроверять асимптоты, интервалы возрастания/убывания, выпуклости/вогнутости. При переходе через левую зелёную точку график начинает плавно выгибаться вверх – и до второй точки
у нас интервал выпуклости. Затем снова следует плавный прогиб вниз и на крайнем правом интервале имеет место вогнутость графика.
Более простое задание для самостоятельного решения:
Найти интервалы выпуклости, вогнутости и точки перегиба графика
Особенность предложенной функции состоит в её чётности, а это значит, что интервалы выпуклости/вогнутости и точки перегибы графика (если они существуют) симметричны относительно оси . И если, например, на крайнем левом интервале получится выпуклость, а на крайнем правом вогнутость, следовательно, где-то допущена ошибка. Примерный образец решения + чертёж для наглядности – в конце урока.
Читателям со средним и высоким уровнем подготовки (да и чайникам тоже) рекомендую попутно исследовать возрастание/убывание и экстремумы функций – ведь в рассматриваемых заданиях вынужденно фигурируют первые производные! Комплексный подход быстрее научит проводить полное исследование функций и понимать, как выглядят их графики.
Настал черёд популярных…, правильно догадались, дробно-рациональных:
Исследовать график функции на выпуклость, вогнутость и перегибы.
Решение:
1) Функция терпит бесконечные разрывы в точках , и это обстоятельство крайне важно для решения задачи.
2) Найдём критические точки второй производной.
Пополните свой арсенал рациональной методикой упрощения второй производной: числитель и знаменатель сокращаем на , множитель выносим за скобки. А в случае возникновения трудностей с нахождением самих производных, целесообразно перебазироваться в соседний раздел сайта и поднять свою технику дифференцирования.
В результате получена одна критическая точка: .
Теперь анализируем множители:
Итак, какую информацию нам предоставила ?
Ответ: график функции является вогнутым на и выпуклым на . В начале координат (ясно, что ) существует перегиб графика.
При переходе через точки вторая производная тоже меняет знак, но они не считаются точками перегиба, так как функция терпит в них бесконечные разрывы.
В разобранном примере первая производная сообщает нам о росте функции на всей области определения. Всегда бы такая халява =) Кроме того, очевидно наличие трёх асимптот . Данных получено много, что позволяет с высокой степенью достоверности представить внешний вид графика. До кучи, функция ещё и нечётная. Исходя из установленных фактов, попытайтесь выполнить набросок на черновике. Картинка в конце урока.
Задание для самостоятельного решения:
Исследовать график функции на выпуклость, вогнутость и найти точки перегиба графика, если они существует.
Чертежа в образце нет, но гипотезу выдвинуть не возбраняется ;)
Шлифуем материал, не нумеруя пункты алгоритма:
Исследовать график функции на выпуклость, вогнутость и найти точки перегиба, если они существует.
Решение: функция терпит бесконечный разрыв в точке .
У нас как обычно, всё отлично:

Определим знаки на полученных интервалах:
В точке существует перегиб графика, найдём ординату точки:
При переходе через точку вторая производная не меняет знак, следовательно, в ней НЕТ перегиба графика.
Ответ: интервалы выпуклости: ; интервал вогнутости: ; точка перегиба: .
Рассмотрим заключительные примеры с дополнительными примочками:
Найти интервалы выпуклости, вогнутости и точки перегиба графика
Решение: с нахождением области определения особых проблем не возникает:
, при этом в точках функция терпит разрывы.
Идём проторенной дорогой:

Определим знаки , при этом рассматриваем интервалы только из области определения функции:
В точке существует перегиб графика, вычислим ординату:
Ответ: график является выпуклым на и вогнутым на , в точке существует перегиб.
Сильно маньячить не будем – то же задание для функции .
Рекомендую следующий порядок действий:
– В методичке Графики элементарных функций ищем график арккосинуса. Думаю, интервалы выпуклости/вогнутости и точку перегиба видно неплохо.
– В принципе, понятна и , но её академичнее найти аналитическим путём. Похожие примеры разобраны в конце урока Область определения функции.
– На завершающем этапе, собственно, выполняем задание, при этом поведение второй производной нужно изучить только в найденной области определения функции .
Полное решение и ответ в конце урока.
Как отмечалось в теоретической части статьи, бывает ситуация, когда функция определена в некоторой точке, однако вторая производная в ней не определена. Такая точка считается критической (но только один этот факт и здесь не гарантирует наличие перегиба!).
Например, график функции терпит перегиб в начале координат, хотя второй производной там не существует. Тем не менее, в точке строго выполнено и необходимое и достаточное условие перегиба. Желающие могут убедиться в этом самостоятельно.
Похожий случай с более трудной функцией и её первой производной рассмотрен в Примере 8 урока об экстремумах функции (откройте на соседней вкладке – там есть график). Не поленился, прямо сейчас нашёл (вроде как правильно). На числовой прямой откладываем выколотые критические точки второй производной. Анализ на полученных интервалах показывает, что при переходе через точку (остриё) знак 2-й производной не меняется (перегиба нет), а вот в точке есть перегиб графика (хотя и не существует).
Теперь у вас есть всё необходимое оружие и доспехи для генерального сражения с графиками функций!
Решения и ответы:

Пример 2: Решение:
1) Функция терпит бесконечный разрыв в точке
2) Найдём критические точки второй производной:
Критические точки отсутствуют.
3) Определим знаки второй производной на полученных интервалах:
Ответ: график функции является вогнутым на интервале и выпуклым на , точки перегиба отсутствуют.
Пример 4: Решение:
1) Функция определена и непрерывна на .
2) Найдём критические точки второй производной:
– критические точки
3) Определим знаки второй производной на полученных интервалах:
В точках существуют перегибы графика.
Ответ: график функции является вогнутым на интервале и выпуклым на , точки перегиба: .
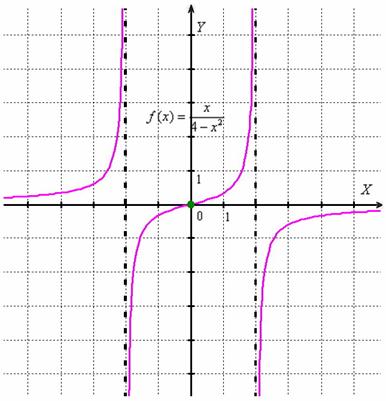
График Примера 5:

Пример 6: Решение: найдём критические точки второй производной:
– критические точки:
Определим знаки второй производной на полученных интервалах:
Во всех трёх точках существуют перегибы графика.
Ответ: график функции выпуклый на и вогнутый на . В точках существуют перегибы графика.

Пример 9: Решение: найдём область определения функции. Составим и решим двойное неравенство:
Таким образом, .
Найдём критические точки второй производной:
– критическая точка.
Учитывая область определения функции, определим знаки :
В точке существует перегиб графика.
Ответ: интервал вогнутости графика: , выпуклости: , точка перегиба: .
Автор: Емелин Александр
(Переход на главную страницу)
cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5
Читайте также:
- Журнал регистрации телефонограмм в доу образец
- Практические и теоретические проблемы жизненная философия и школьная философия
- Сценарий новогоднего праздника для начальной школы с конкурсами и играми 4 класс
- Навигатор дополнительного образования детей оренбургской области инструкция для школ
- Охарактеризуйте основные признаки правовой нормы дайте ей определение кратко

