Технология задачного обучения кратко

Обновлено: 26.07.2024

Корабль образования должен двигаться галсами, ибо движение в одном направлении либо приведёт его в тупик, либо посадит на мель. 30 лет назад реформа математического образования, контуры которой задал А.Н.Колмогоров, приняла одно из возможных направлений. Наступило время сделать очередной галс. Речь ни в коем случае не должна идти об отказе от уже сделанного, о возврате назад, а лишь о некотором повороте, отражающем произошедшие за это время кардинальные изменения в обществе. Из чего исходить при выборе нового направления?

Сегодня мы живём в других социально-политических реалиях. Если раньше истина директивно задавалась с верху и была единственной, то сегодня одни и те же явления могут оцениваться с различных точек зрения – монополии на истину не существует.
Происходит глобализация восприятия мира. Мы начинаем острее воспринимать сложность и взаимосвязанность идущих в природе и обществе процессов, в том числе и явлений самоорганизации.
Резко изменилась и продолжает меняться информационная среда. Человеку, находящемуся в лавинах информационных потоков, необходимо научиться быстро, перерабатывать огромный объём зачастую противоречивой информации, адаптироваться в этих условиях.

Всё это показывает необходимость более решительно подходить к реформе математического образования, прекратить топтаться на месте, поскольку математическое образование наиболее способствует:

изучению физики, химии, биологии, экономики, астрономии, информатики и др.;
развитию порядочности и самостоятельности в здоровой социальной среде;
успешному продолжению образования;
воспитанию профессиональных качеств при овладении любой профессией;
развитию эстетических чувств (красивый факт, красивая задача или решение, изящное доказательство.

Математика универсальна, всеобща, приобщает к мировой культуре именно потому не существует национальной, ведомственной или государственной математики.

Всё это заставляет задуматься о возможности осторожных и продуманных изменений как в содержании, так и в методических технологиях школьного математического образования. Одной из таких технологий является – система задач и задачный подход к обучению.

Самое главное найти у каждого ученика мотив к учению и самое трудное в работе учителя поиск необходимых инструментов прикосновения к личности. Как сформировать у учащихся интерес к предмету, научить самостоятельно и творчески добывать знания, активно участвовать в процессе обучения, уметь анализировать и оценивать свои знания – эти вопросы волновали меня как учителя. Помогла технология постановки целей (М.Е.Бершадский, В.В.Гузеев) – система задач и задачный подход к обучению.

Методы нахождения решений и психическая деятельность, связанная с поиском решения, во многом сходны как в жизненных или производственных задачах, так и в школьных (по математике, физике, химии). Поэтому ознакомление учащихся с методами поиска решений является средством не только улучшения учебных навыков, но и воспитания учащихся, подготовки их к будущей производственной деятельности, к жизни. От эффективности применения задач в обучении математике во многом зависит и степень подготовленности школьников к практической деятельности в любой сфере производства, народного хозяйства и культуры.

Решая математические задачи, представленные в продуманной системе, учащиеся не только активно овладевают содержанием курса математики, но и приобретают умения мыслить творчески. Это проявляется, например, в умении изменить условие задачи с целью применить тот или иной метод, приём в умении изобретать новые приёмы для решения задач; в умении выделять и накапливать потенциально полезную информацию; умение конструировать на базе данной задачи новые; в умении осуществлять самоконтроль, исследовать результат решения.

Поэтому можно утверждать, что педагогические основы использования задач в современном школьном обучении правомерно являются тем средством обучения, без применения которого невозможно активное и прочное усвоение учащимися программного материала, их всестороннее воспитание и развитие, приобщение к труду творческого характера.

Многие задачи, которые решаются на уроках математики и других предметов, можно условно подразделить на шаблонные и нешаблонные. Роль первых сводится к выработке навыков, необходимых для решения вторых. Например, учащимся предлагают разложить на множители выражение x 3 + y 3 . Это шаблонное упражнение. Не умея его выполнить, учащийся X класса не сможет упростить выражение sin 6 α + cos 6 α + 3cos 2 α sin 2 α. Последнее упражнение можно считать нешаблонным. Вообще, указанная классификация условна и проводится на основе не математических, а дидактических соображений. Рассмотрим следующую задачу (которая может быть поставлена перед учащимися VII- IX классов): Найти натуральные числа x, y, z, если xyz + xy + yz + + xz + x + y + z = 1975. Решение этой задачи достигается разложением на множители числа 1976 и одновременно увеличением на 1 левой части равенства: (x + 1)(y + 1)(z + 1) = 2 3 · 13 · 19. Используя условие: x, y, z – натуральные числа, нетрудно найти возможные решения. Решение этой задачи не требует от учащихся знаний внепрограммного материала; вместе с тем задача направлена на глубокое понимание изученного, на формирование у школьников умения творчески применять известные знания.

По традиции в школьной практике в одних случаях осуществляется постепенный переход от метода шаблонных задач к методу нешаблонных, а в других такой постепенный переход не соблюдается. Когда не соблюдается постепенный переход от метода шаблонных задач к методу нешаблонных, нарушаются дидактические принципы последовательного преодоления трудностей, доступности, что приводит к плохим знаниям. Осуществляя постепенный переход от метода шаблонных задач к методу нешаблонных, ускоряя такой переход в случае работы с сильными классами, и, наоборот, переходя к простейшим, порой примитивнейшим упражнениям в слабых классах, отрабатывая в последних умения и навыки проведения тех преобразований, вычислений и рассуждений, которыми должны были обладать учащиеся, но, к сожалению, не обладают, мы всегда можем осуществить дидактические принципы последовательного преодоления трудностей, доступности, полноты, сравнения и т.д.

Ныне действующие программы по математике не предусматривают изучение каких-либо теоретических основ о задачах и их решении. Теоретические знания о задачах и их решении нужны учащимся для того, чтобы они могли производить решение разнообразных задач сознательно и целенаправленно, а не только лишь на основе подражания, по аналогии с ранее решёнными задачами. Конечно, такие аналогии нужны, но если ученик при встрече с незнакомой задачей ограничивается лишь поиском аналогий, то неминуемы ошибки, а в большинстве случаев решение вовсе не будет найдено. Поиск решения незнакомых задач должен вестись школьниками культурно и сознательно, с полным пониманием сущности самой задачи и её решения. Важнейшими элементами любого метода поиска решения являются анализ и синтез. При решении математических задач синтез может использоваться в двух формах рассуждения: 1) когда двигаются от данных к искомым фактам; 2) когда элементы объединяют в одно целое. Точно так же и анализ может выступать в двух формах: 1) когда в рассуждениях двигаются от искомых к данным задачи; 2) когда целое (фигуру, выражение и т.п.) расчленяют на части.

6. Старайтесь научить своих учеников догадываться.
7. Старайтесь научить своих учеников доказывать.
10. Пользуйтесь наводящими указаниями, но не старайтесь навязывать своего мнения насильно.

В каждом способе решения задач какого-либо вида, в самом решении этих задач, в умениях, формируемых при этом, содержатся как чисто специфические черты, присущие лишь способу и умениям, соответствующим данному виду задачи, так и некоторые общие черты, присущие методам и умениям по решению любых математических задач. Поэтому при решении задач того или иного вида надо в первую очередь подчёркивать и выделять общие методы решения задач: разбиение на подзадачи, разбиение области задачи на части, сведение данной задачи к ранее решённым, модельные преобразования задачи.

Значит, задача учителя состоит в следующем: сформировать такой общий подход к решению задач, когда задача рассматривается как объект для анализа, для исследования, а её решение – как конструирование и изобретение способа решения. Естественно, что такой подход требует не бездумного решения огромного числа задач, а неторопливого, внимательного и обстоятельного решения значительно меньшего числа задач, но с серьёзным последующим анализом проведённого решения, выявления в нём общих методов и приёмов решения любых математических задач.

Главное при этом – разбудить дремлющие силы самого ученика, вызвать у него ненасыщаемую жажду знаний, желание самосовершенствования.

Задачный подход к обучению имеет свои закономерности, принципы, правила и требования. Они являются ориентиром в моей работе. К ним относятся: полнота, наличие ключевых задач, связность, возрастание трудности в каждом уровне, целевая ориентация, целевая достаточность, гибкость, психологическая комфортность.

1. Полнота. Наличие задач на все изучаемые понятия, факты, способы деятельности, включая мотивационные, подводящие под понятие, на аналогию, следствие из фактов.

2. Наличие ключевых задач. Группировка задач в узлы вокруг объединяющих центров – задач, в которых рассматриваются факты или способы деятельности, применяемые для решения других задач и имеющие принципиальное значение для усвоения предметного содержания.

3. Связность. Вся совокупность задач графически может быть представлена связным графом, в узлах которого – ключевые задачи, выше них – подготовительные и вспомогательные, ниже – следствия, обобщения и так далее.

4. Возрастание трудности на каждом уровне. Система задач состоит из трёх подсистем, соответствующих минимальному, общему и продвинутому уровням планируемых результатов обучения. В каждой из подсистем трудность задач непрерывно нарастает.

5. Целевая ориентация. Для каждой задачи определено её место и назначение в блоке уроков.

6. Целевая достаточность. Достаточно задач для тренажа в классе и дома, аналогичных задач для закрепления методов решения, задач для групповых и индивидуальных заданий разной направленности, задач для самостоятельной (в том числе и исследовательской) деятельности учащихся, задач для текущего итогового контроля с учётом запасных вариантов.

7. Гибкость. Гибкость задачного подхода выражается в обеспечении возможности приспособления содержания обучения и путей его усвоения к индивидуальным потребностям обучаемых. Надо обеспечить индивидуальный темп усвоения, индивидуальную технологию обучения.

8. Психологическая комфортность. Система задач учитывает наличие разных темпераментов, типов мышления, видов памяти. Есть задачи для устных упражнений, письменного выполнения, чтение чертежа, задачи-шутки и другие. Каждое задание, предлагаемое учителем (там, где это возможно), должно иметь словесное, графическое, предметно-иллюстративное решение. Ученик вправе выбрать какое-либо одно и может рассчитывать на успех, что будет усиливать его учебную мотивацию. Это особенно важно в старших классах, где дидактический материал разнообразен по содержанию, форме и объёму.

Рассмотрим всё выше сказанное на примерах.

Предлагаю решить неравенство: (а+2)(а+3)≥0.

Решением его является объединение двух промежутков (-∞;- 3) (- 2; +∞).

Далее предлагаю решить методом интервалов другие неравенства. Но так, чтобы, видоизменяя неравенство можно было увидеть, и как изменяется его решение.

Полезно также предложить учащимся неравенства, которые решаются по смыслу:

Ранее рассмотренные неравенства можно использовать для решения уравнений.

, очевидно, что при всех значениях а , удовлетворяющих неравенству (а+2)(а+3) >0, уравнение имеет смысл.

Упражнения, которые составляются и решаются по аналогии

Другими словами, мы находим общий способ решения различных по заданию задач.

Например, решаем уравнение с одной переменной (х 2 – 4х + 3) 2 + (х 2 – 1,5х + 0,5) 2 = 0.

Равенство верно, если

х 2 – 4х + 3 = 0;
х 2 – 1,5х + 0,5 = 0. Отсюда, х = 1.

Затем можно дать уравнение с двумя переменными, которые решаются аналогично первому:

1) (х 2 – 4х + 3) 2 + (у 2 – 5у +6) 2 = 0;
2) (х 2 - у – 2) 2 + (х + у +2) 2 = 0.

Если предложить учащимся решить квадратное уравнение с двумя переменными типа

3) х 2 + у 2 + 6х – 2у + 10 = 0 после решения квадратных уравнений с одной переменной, то обычно они испытывают трудность в поиске его решения, но если им предложить это уравнение после решения уравнений 1) и 2), то ученики легко находят способ решения, рассуждая по аналогии. Действительно, для этого достаточно привести уравнение (3) к виду: (х 2 + 6х + 9) + (у 2 – 2у + 1) = 0, (х + 3) 2 + (у – 1) 2 = 0.

Затем логично взять примеры на доказательство. Доказать, что квадратный трёхчлен х 2 – 6х + 9,25 положителен при все значениях х . Учащиеся, по аналогии, выделив полный квадрат, легко приведут трёхчлен к виду (х – 3) 2 + 0,25 и сделают вывод. Что квадратный трёхчлен положителен при всех х. Затем полезно предложить учащимся многочлен с двумя переменным и доказать, что при всех х и у, он принимает лишь положительные значения: 2х 2 + 5у 2 + 2ху + 1 = (х 2 +2ху + у 2 ) + (4у 2 + х 2 + 1) = (х + у) 2 +(4у 2 + х 2 + 1).

(х + у) 2 ≥0 и (4у 2 + х 2 + 1)>0 при всех значениях переменных. Следовательно, 2х 2 + 5у 2 + 2ху + 1 >0.

Подобный подход к осмыслению материала уроков позволяет найти не только общие методы решения задач, но и способы уплотнения урока.

Задачный подход к обучению можно использовать в каждом классе, каждым учителем. Этот подход позволяет поверить ученику в свои силы, совместная работа учителя и ученика даёт эффект сотрудничества, позволяет видеть своё продвижение по мере нарастания трудности задач. При этом способе работы возможно разноуровневое (дифференцированное) обучение: для сильных учащихся задачи продвинутого уровня, больший объём теоретического материала, работа с дополнительными учебниками, задачниками; для слабых – задачи минимального уровня, больше помощи со стороны учителя.

Свидетельство и скидка на обучение каждому участнику

Зарегистрироваться 15–17 марта 2022 г.

Задачный подход к обучению.

Социальные преобразования, происходящие в обществе, требуют модернизации образования, то есть создания новой образовательной модели. в которой взаимосвязь деятельности учителя и деятельности учащихся рассматривается с точки зрения задачного подхода обучения, при котором создаются условия для развития познавательной деятельности учащихся.

Сущность задачного подхода к обучению.

В отличие от традиционного подхода к обучению задачный подход:

1. Выбирает приоритетом к обучению - решение учебных задач, результатом, которых являются сформированные обобщённые умения, имеющие сложный операционный состав.

2. Позволяет мотивировать и активизировать учебную деятельность учащихся.

3. Формирует личность, способную к самостоятельной творческой деятельности.

Теперь осуществим задачный подход. Учитель ставит перед учащимися следующую учебную задачу. В давние времена у берегов Японии случилась такая история. Несколько шхун везли вазы из тончайшего фарфора во дворец императора. По дороге их застиг шторм, и все шхуны утонули. Это произошло недалеко от берега, где стояли хижины бедных рыбаков. Вазы стоили очень дорого, поэтому многие смельчаки пытались достать их. Но это не удавалось никому – слишком велика глубина для ныряльщиков, а подводных аппаратов тогда не знали. А один местный рыбак попробовал использовать для подъёма затонувшего груза осьминогов. Удалось ли поднять груз?

Задачная методическая модель системы обучения.

Предметные задачи обеспечивают усвоение понятий и ориентировку в изучаемой теме. Практико – ориетированные задачи раскрывают связь предмета с практической жизнью человека. Личностно – ориентированные задачи вводят учащихся в сферу мировоззренческих проблем бытия, требующих от него проявления личностной позиции.

Например: На аэродроме 20 самолётов. Сколько троек самолётов поднялось в воздух, если несколько самолётов остались на земле?

Далее следует рассмотреть все возможные варианты количества троек взлетевших самолётов. Решение этой задачи можно записать в таблицу (см. слайд).

В заключение решения важно обратить внимание учащихся, что задача имеет не один ответ.

При реализации задачного подхода изучаемый материал представляется в виде системы задач, включающих ориентировку в самом предмете, в сфере его компетентного применения и в ценностно – смысловых аспектах бытия, связанных с изучаемым предметом. Чтобы учебная задача вызывала познавательную активность ученика, он должен увидеть личностный смысла.

З адачный подход направлен на саморазвитие, самообразование и совершенствование учебного процесса. Использование системы взаимосвязанных учебных задач в современном образовании является тем средством обучения, которое способствует активному и прочному усвоению учащимися программного материала, их всестороннему воспитанию и развитию, приобщению к труду творческого характера.

Ученик должен быть поставлен в условия поиска, заблуждений, радостных открытий и огорчений от временных неудач. Мышление начинается там, где есть неизвестное, где встречаются затруднение, непонимание, ошибка. А, следовательно, учитель так продумывает урок, что поставленные учебные цели подразделяются на ряд учебных задач, решаемых учащимися совместно или самостоятельно.

Еще великий Сократ отмечал, что

Специально организованное, правильно и систематически осуществляемое обучение в виде разрешения разнообразных учебных задач расширяет возможности обучения.

При этом существенно развиваются волевая и мотивационная сферы учебной деятельности и в некоторой степени эмоционально-чувственная.

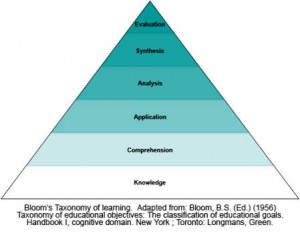
Имеющиеся таксономии учебных целей, и особенно таксономия Б. Блума, широко используются в образовательных технологиях при построении системы типовых задач для определения конкретных умений учащихся. М.Е. Бершадский и М.Е. Гузеев приводят конкретный пример заданий для школьников из различных предметных областей, по результатам которых можно судить о различных уровнях обученности.

Примеры задач для различных уровней учебных целей

в познавательной области по Бенджамину Блуму.

Знание.

Дайте определение имени существительного.
Когда и где разворачивается действие рассказа и когда в тексте это становится ясно?
На какие две категории можно разделить все живые существа?
Вычислите значение выражения (9-177)/21+8.
Назовите палаты Федерального Собрания Российской Федерации.

Понимание.

Расскажите, что произошло с героями романа после эпизода, изображенного на иллюстрации.
Нарисуйте три картинки о событиях, которые происходили в начале, середине, и конце XIX века в Германии.
Расскажите коротко своими словами содержание параграфа.
Напишите сочинение (две-три страницы) с описанием обязанностей президента.
Приведите примеры того, как в рассказе подтверждается, что Даниле не безразличны чувства других людей.
Почему на географических картах используются символы?

Применение.

Составьте предложение с использованием каждого из данных слов.
Изучив знаки на картах, составьте план маршрута для посещения трех исторических памятников в Подмосковье.
Найдите площадь класса, в котором вы занимаетесь.
Теперь, когда вы прочли почти весь рассказ, угадайте, чем он закончится.
Придумайте три практических ситуации, в которых вы сможете использовать изученный способ определения влажности.

Анализ.

Какие события в этой истории действительно имели место, а какие выдуманы автором?
Чем период после гражданской войны напоминает период после войны в Афганистане, и чем они отличаются?
Распределите минералы этой коллекции по трем категориям.
Среди утверждений разбираемой статьи укажите три, которые являются фактами, и три, которые являются мнениями.
По описаниям десяти насекомых определите, к какому семейству относится каждое из них.
Какие из данных слов имеют латинское происхождение, а какие – греческое?

Синтез.

Оценка.

Обязательно ли должны все кандидаты на пост мэра Екатеринбурга иметь высшее образование?
Сравните двух главных героев поэмы.
Нужно ли требовать от школьников навыков устных вычислений в век недорогих калькуляторов? Почему?
Оправдано ли насилие для исправления несправедливости? Объясните вашу позицию.
Какая среда из всех изученных вам больше нравится для жизни? Аргументируйте свой ответ.
В каких случаях демократическое устройство государства менее эффективно, чем диктатура?

(Б.Е. Бершадский, В.В. Гузеев. Дидактические и психологические основания образовательной технологии. М.,2003. С. 144-146.)

В то же время некоторые из заданий, к примеру, на применение можно было бы отнести к уровню анализа или даже оценки. Во всяком случае, создатели различных образовательных технологий, как правило, стремятся к разработке собственных таксономий учебных задач.

При всем разнообразии подходов привлекает внимание стремление специалистов с помощью таксономии проследить весь учебный процесс, создать систему учебного мониторинга не только для определения достижений учащихся, но и динамики всего учебного процесса.

Одной из наиболее популярных является разработка известного чешского ученого Даны Толлингеровой, которая, опираясь на таксономию учебных целей Б. Блума, предложила таксономию учебных задач, разделенных на 5 категорий, содержащих 27 типов учебных задач по операционной структуре, то есть по операциям, необходимым для их выполнения.

Полнота и детальная разработанность таксономии учебных задач, а также то обстоятельство, что задания в ней упорядочены по когнитивной сложности и сопоставлены с количественным показателем (тип задач), позволяет использовать эту таксономию не только как оценочную шкалу, но и для разработки алгоритма учебных действий.

ТАКСОНОМИЯ УЧЕБНЫХ ЗАДАЧ ПО Д. ТОЛЛИНГЕРОВОЙ

1. Задачи, требующие мнемического воспроизведения данных:

Задачи по узнаванию.
Задачи по воспроизведению отдельных фактов, чисел, понятий.
Задачи по воспроизведению дефиниций, норм, правил.
Задачи по воспроизведению больших текстов, блоков, стихов, таблиц и т.п.

2. Задачи, требующие простых мыслительных операций с данными:

Задачи по выявлению фактов (измерение, взвешивание, простые исчисления и т.п.).
Задачи по перечислению и описанию фактов (исчисление, перечень и т.п.).
Задачи по перечислению и описанию процессов и способов действий.
Задачи по разбору и структуре (анализ и синтез).
Задачи по сопоставлению и различению (сравнение и разделение),
Задачи по распределению (категоризация и классификация).
Задачи по выявлению взаимоотношений между фактами (причина, следствие, цель, средство, влияние, функция, полезность, инструмент, способ и т.п.).
Задачи по абстракции, конкретизации и обобщению.
Решение несложных примеров (с неизвестными величинами и т.д.)

3. Задачи, требующие сложных мыслительных операций с данными:

Задачи по переносу (трансляция, трансформация).
Задачи по изложению (интерпретация, разъяснение смысла, значения, обоснование).
Задачи по индукции.
Задачи по дедукции.
Задачи по доказыванию (аргументацией и проверке (верификации))
Задачи по оценке.

Задачи по разработке обзоров, конспектов, содержания и т.д.
Задачи по разработке отчетов, трактатов, докладов и т.п.
Самостоятельные письменные работы, чертежи, проекты и т.п.

5. Задачи, требующие творческого мышления.

Задачи по практическому приложению.
Решение проблемных задач и ситуаций.
Постановка вопросов и формулировка задач или заданий.
Задачи по обнаружению на основании собственных наблюдений (на сенсорной основе).
Задачи по обнаружению на основании собственных размышлений (на рациональной основе)

К первой категории относятся задачи, требующие от учащегося мнемических операций, содержание которых предусматривает узнавание операций, содержание которых предусматривает узнавание или репродукцию отдельных фактов или их целого. Чаще всего они начинаются со слов:

Во вторую категорию включены задачи, при решении которых уже необходимы элементарные операции. Это задачи по выявлению, перечислению, сопоставлению, обобщению и т.п. Начинаются они обычно словами:

Третья категория охватывает задачи, решение которых требует сложных мыслительных операций.

Сюда относятся задачи по индукции, дедукции, интерпретации, верификации и др. Начинаются они обычно со слов:

В четвертую категорию включены задачи, предусматривающие для их решения помимо мыслительных операций еще какой-нибудь речевой акт, устный или письменный. Следовательно, сюда относятся все задачи, требующие не только проведение определенных операций, но и высказываний о них. Учащийся в этих задачах дает показание не только о результате решения, но также и о его ходе, условиях, фазах, компонентах, трудностях и т.д.

В пятую категорию входят задачи, которые предполагают самостоятельность при решении задач. Начинаются они обычно словами:

Это уже задачи, которые предполагают не только знание всех предшествующих операций, но и способность комбинировать их в большие блоки, структуры, секвенции, стратегии и пр. так, чтобы они создавали нечто новое, пусть даже только субъектно, то есть для учащегося, новое.

Дидактическая ценность системы учебных задач, по мнению Д.Толлингеровой, связана с выполнением поставленной педагогической цели:

если целью учителя было проверить знания учащегося, то достаточно, чтобы тест содержал задачи первой категории,
если же цель — проверить, как учащийся использует сложные мыслительные операции, то задачи 1-2 категорий не позволят гарантировать достижения поставленной цели.

При этом, сравнительно разнородный набор задач, где чередуются разные познавательные операции, предотвращает демотивацию учащихся под влиянием монотонности задаваемых задач.

Как видим, все задачи, предложенные Д. Толлингеровой, проранжированы по возрастанию когнитивной сложности и операциональной ценности. Система запланированных целей неразрывно связана с системой действий, которые ведут к выполнению этих целей.

Таким образом, с использованием таксономии можно конструировать систему учебных задач для выполнения поставленных педагогических целей, более полно учитывать состав когнитивных требований к учебной ситуации, проводить диагностику знаний и уровня сформированности учебных действий учащихся, а также прогнозировать ход обучения с учетом меры сложности задач и степени нагрузки на все виды проектируемой познавательной деятельности, то есть можно создавать индивидуальную программу развития обучаемых или более эффективно организовывать дифференцированную работу.

По мнению Д.Толлингеровой, главная задача учителя — научиться составлять учебные задачи так, чтобы их операционная структура соответствовала преследуемым педагогическим целям и учебному материалу:

Таксономия учебных задач.

Русский язык. 3 класс. (Программа 1-4). Составлено учительницей начальных классов средней школы №6 г. Армавира АСТВАЦАТУРОВОЙ Т.П.

Тема: Род имен существительных. Изменение имен существительных по числам и падежам.

I. Задания первого уровня направлены на развитие памяти и формирование репродуктивных знаний.

1. Слова, которые обозначают предметы и отвечают на вопросы _______ или __________ называются ____________

2. Существительные бывают _____________ и ______________ рода

3. Существительные изменяются по _____________ и по________________. В единственном числе по _________________

4. Сколько падежей в русском языке? _______

5. Вставь пропущенные буквы:

Ябл.ко, земл.ника, .зык, т.традь, мес.ц, уржай, п.м.дор, яг.да, п.года, к.рабль, м.л.ток, д.рога, р.бина.

6. Вставь подходящие по смыслу имена существительные, чтобы получился рассказ про зайца.

Этот пушистый … живет в ..

У него длинные ___________, короткий _____ и косые ___________

Сладкая___________ и хрустящая __________ — любимые лакомства __________ . А зимой и горькая __________ хороша.

Маленький ____ всего боится.

Слова для справок: зайчик, уши, глаза, хвост, лес, морковь, капуста, животное, кора, зверек.

II. Задания второго уровня направлены на умение трансформировать репродуктивные знания.

1. Определи род имен существительных: Муравей (…), ружье (…), квартира (…), кастрюля (…), болото (…), магазин (…), платок (…), платье (…), лестница (…).

2. Данные имена существительные напиши во множественном числе:

в единственном числе:

Подчеркни правильное утверждение:

4. Просклоняй существительное весна. Выдели окончания.
И. _____________________

5. Укажи падеж выделенных существительных:

Каждое утро мы ходим в школу ( ). В школе ( ) мы уз-тем много нового. Володя сидит за первой партой ( ). Он положил на парту ( ) свои книги.

III. Задания направлены на усвоение мыслительных операций и формирование продуктивных знаний.

1. Подчеркни существительные, которые употребляются только во множественном числе:

столы, штаны, санки, машины, клещи, ножницы, молоко.

2. Знаешь ли ты, как будет множественное число от слов:
человек-

3. Прочитай и образуй новые слова:
Москва — москвич — москвичка.

Укажи род записанных существительных.

4. В каких падежах использовал поэт существительные, создавая свой зимний пейзаж?

На сосне (…) и на березе (…) — бахрома (…). Белой пряжей (…) их запутала зима (…). И оставила распутывать весне (…) Эту пряжу на березе (…) и сосне (…).

Какой падеж отсутствует?

5. Замени одним словом:

Человек, который играет на трубе — ______________

Человек, который выступает в цирке- _______________

Край земли у воды — ____________________

Комментарии к “ Сущность задачного подхода в обучении ”

На уроках английского языка мы также сопоставляем и применяем наши знания на практике. Например: Вставьте предлоги: 1. John is looking ____ a job.
a for
b after
c to

2. Is it the photograph ____ your brother?
a of
b with
c to

интересно и полезно. всё выстраивается в понятную систему, есть желание многое поменять в построении своих уроков. спасибо

Обучение не будет выполнять развивающую функцию, если при решении системы задач деятельность учащихся ограничивается репродуктивными действиями, но не включает механизма собственной аналитико-синтетической деятельности.

Приводим примерный перечень умений по решению задач, которые необходимо развивать у учащихся.

1. Умение анализировать состав задачи (выявление совокупности элементов и описание структурных связей-отношений между ними).

2. Развертывание условий (определение явных и неявных приведенных данных).

4. Умение расширять диапазон эвристик. Эвристики – специальные приемы организации мышления, направленные на создание оптимальных условий проявления интуиции. Знание эвристик развивает способность находить подходы к задачам, методы, решения которых еще неизвестны (выходить за пределы собственных знаний). В качестве эвристик могут выступать: эвристические правила, содержащие рекомендации по выбору возможного действия в условиях альтернативного поиска. Правила включают: а) эвристические сведения (формулы, законы), афоризмы (пословицы, поговорки, крылатые выражения), правила предпочтения; б) эвристические операции – это мыслительные действия, направленные на достижение цели: индукция, аналогия, сравнение, обобщение и т.д.

5. Умение составлять план решения (на основе логико-эвристической деятельности предвидеть и строить последовательность действий).

6. Умение аргументировать действия.

7. Умение выделять обобщенный алгоритм решения (если это возможно).

8. Умение ретроспективного анализа.

Каждый курс определенного предмета можно представить в виде системы познавательных задач. Эта система должна отвечать по крайне мере пяти показателям:

1. В ней должны содержаться задачи, соответствующие иерархии учебных целей, т.е. задачи на первый уровень усвоения – уровень знакомства – различения; задачи второго уровня усвоения – алгоритмического; задачи соответствующие третьему уровню усвоения – творческому.

2. Система задач должна учитывать практически все основные виды структурных связей, возможных в данной области знаний.

4. Система задач должна определять всю типологию методов познания, специфичных для определенной науки. Например, по истории это будут методы: сравнительно-исторический, метод аналогий, статистический метод, метод определения причин по следствиям, метод реконструкции целого по части и наоборот и т.д.

5. Необходимым показателем системы задач является полнота процедур творческой деятельности.

Необходимо конструирование системы задач, обеспечивающей формирование следующих творческих процедур (по И. Я. Лернеру ):

· самостоятельный перенос ранее усвоенных знаний и умений в новую ситуацию;

· видение новой проблемы в знакомой ситуации;

· видение новой функции объекта;

· осознание структуры объекта;

· поиск альтернативных способов решения;

· комбинирование ранее известных способов действий в новый способ.

Анализ задач в школьных учебниках показывает, что часто в задачах к теме превалируют задачи, требующие творческих процедур одного и того же типа (перенос знаний в новую ситуацию). Необходимо разнообразие задач, вычерпывающие все виды творческих процедур.

Деятельность при решении задачи можно разделить на четыре вида: репродуктивная, алгоритмическая, трансформированная и творческо-поисковая. В первом виде деятельности проблемность близка к нулю, а каждый последующий вид должен обладать большим уровнем проблемности . Любой учебный текст может состоять из различного сочетания задач всех названных типов.

Репродуктивные задачи решаются по заданной в словесной форме программе выполнения всех элементарных шагов с указанием условий их применения.

Алгоритмические задачи решаются по алгоритму, заданному в виде формулы, правила, т.е. для решения необходимо, развернуть этот алгоритм, заданный в виде формулы, в развернутую программу. Поэтому при решении такой задачи используются и действия неалгоритмического, проблемного характера.

Интуитивное познание характеризуется, во-первых, неосознанностью, нерасчлененностью процесса с продуктом. Во-вторых, чтобы интуиция являлась целенаправленным процессом, чтобы вызвать подсознательную деятельность, необходимо сознательное предварительное усилие и напряжение. И, в-третьих, интуитивные решения всегда сопровождаются эмоциональной реакцией, т.к. преодоление затруднения, возникающего в проблемной ситуации, снимает эмоциональный дискомфорт.

Преимущества нашего сервиса

1. По ФГОС

Все мероприятия на нашем портале проводятся строго в соответствии с действующим законодательством и ФГОС

2. Быстро

Результаты участия в творческом конкурсе будут оглашены в течение 2 часов с подачи заявки.

3. Честно

Участие в любом конкурсе – бесплатное. Вы оплачиваете изготовление документа только когда знаете результат..

Читайте также: