Таблица пределов функций для школы

Обновлено: 05.07.2024

Теория пределов – это один из разделов математического анализа. Вопрос решения пределов является достаточно обширным, поскольку существуют десятки приемов решений пределов различных видов. Существуют десятки нюансов и хитростей, позволяющих решить тот или иной предел. Тем не менее, мы все-таки попробуем разобраться в основных типах пределов, которые наиболее часто встречаются на практике.

Начнем с самого понятия предела. Но сначала краткая историческая справка. Жил-был в 19 веке француз Огюстен Луи Коши, который дал строгие определения многим понятиям матана и заложил его основы. Надо сказать, этот уважаемый математик снился, снится и будет сниться в кошмарных снах всем студентам физико-математических факультетов, так как доказал огромное количество теорем математического анализа, причём одна теорема убойнее другой. В этой связи мы пока не будем рассматривать определение предела по Коши, а попытаемся сделать две вещи:

1. Понять, что такое предел.
2. Научиться решать основные типы пределов.

Прошу прощения за некоторую ненаучность объяснений, важно чтобы материал был понятен даже чайнику, что, собственно, и является задачей проекта.

Итак, что же такое предел?

А сразу пример, чего бабушку лохматить….

Любой предел состоит из трех частей:

Как решить вышерассмотренный пример? Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:

Итак, первое правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

Мы рассмотрели простейший предел, но и такие встречаются на практике, причем, не так уж редко!

Пример с бесконечностью:

Разбираемся, что такое ? Это тот случай, когда неограниченно возрастает, то есть: сначала , потом , потом , затем и так далее до бесконечности.

А что в это время происходит с функцией ?
, , , …

Итак: если , то функция стремится к минус бесконечности:

Еще один пример с бесконечностью:

Опять начинаем увеличивать до бесконечности и смотрим на поведение функции:

Вывод: при функция неограниченно возрастает:

И еще серия примеров:

Пожалуйста, попытайтесь самостоятельно мысленно проанализировать нижеследующее и запомните простейшие виды пределов:

, , , , , , , , ,
Если где-нибудь есть сомнения, то можете взять в руки калькулятор и немного потренироваться.
В том случае, если , попробуйте построить последовательность , , . Если , то , , .

! Примечание: строго говоря, такой подход с построением последовательностей из нескольких чисел некорректен, но для понимания простейших примеров вполне подойдет.

Что нужно запомнить и понять из вышесказанного?

1) Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

2) Вы должны понимать и сразу решать простейшие пределы, такие как , , и т.д.

Более того, у предела есть очень хороший геометрический смысл. Для лучшего понимания темы рекомендую ознакомиться с методическим материалом Графики и свойства элементарных функций. После прочтения этой статьи вы не только окончательно поймете, что такое предел, но и познакомитесь с интересными случаями, когда предела функции вообще не существует!

На практике, к сожалению, подарков немного. А поэтому переходим к рассмотрению более сложных пределов. Кстати, по этой теме есть интенсивный курс в pdf-формате, который особенно полезен, если у Вас ОЧЕНЬ мало времени на подготовку. Но материалы сайта, разумеется, не хуже:

Пределы с неопределенностью вида и метод их решения

Сейчас мы рассмотрим группу пределов, когда , а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены

Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида . Можно было бы подумать, что , и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим.

Как решать пределы данного типа?

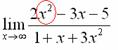
Сначала мы смотрим на числитель и находим в старшей степени:

Старшая степень в числителе равна двум.

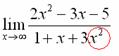
Теперь смотрим на знаменатель и тоже находим в старшей степени:

Старшая степень знаменателя равна двум.

Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.

Итак, метод решения следующий: для того, чтобы раскрыть неопределенность необходимо разделить числитель и знаменатель на в старшей степени.

Разделим числитель и знаменатель на

Вот оно как, ответ , а вовсе не бесконечность.

Что принципиально важно в оформлении решения?

Во-первых, указываем неопределенность, если она есть.

Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак , он не несет никакого математического смысла, а обозначает, что решение прервано для промежуточного объяснения.

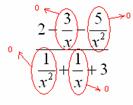
В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так:

Для пометок лучше использовать простой карандаш.

Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметит недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо?

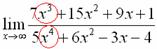
Найти предел
Снова в числителе и знаменателе находим в старшей степени:

Максимальная степень в числителе: 3
Максимальная степень в знаменателе: 4
Выбираем наибольшее значение, в данном случае четверку.
Согласно нашему алгоритму, для раскрытия неопределенности делим числитель и знаменатель на .
Полное оформление задания может выглядеть так:

Разделим числитель и знаменатель на

Под записью подразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число.

Таким образом, при раскрытии неопределенности вида у нас может получиться конечное число, ноль или бесконечность.

Пределы с неопределенностью вида и метод их решения

Решить предел
Сначала попробуем подставить -1 в дробь:

В данном случае получена так называемая неопределенность .

Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида , то для ее раскрытия нужно разложить числитель и знаменатель на множители.

Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения. Если данные вещи позабылись, тогда посетите страницу Математические формулы и таблицы и ознакомьтесь с методическим материалом Горячие формулы школьного курса математики. Кстати его лучше всего распечатать, требуется очень часто, да и информация с бумаги усваивается лучше.

Итак, решаем наш предел

Разложим числитель и знаменатель на множители

Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение:

Сначала находим дискриминант:

И квадратный корень из него: .

В случае если дискриминант большой, например 361, используем калькулятор, функция извлечения квадратного корня есть на самом простом калькуляторе.

! Если корень не извлекается нацело (получается дробное число с запятой), очень вероятно, что дискриминант вычислен неверно либо в задании опечатка.

Далее находим корни:

Всё. Числитель на множители разложен.

Знаменатель. Знаменатель уже является простейшим множителем, и упростить его никак нельзя.

Очевидно, что можно сократить на :

Теперь и подставляем -1 в выражение, которое осталось под знаком предела:

Естественно, в контрольной работе, на зачете, экзамене так подробно решение никогда не расписывают. В чистовом варианте оформление должно выглядеть примерно так:

Разложим числитель на множители.

Разложим числитель и знаменатель на множители.

Что важного в данном примере?
Во-первых, Вы должны хорошо понимать, как раскрыт числитель, сначала мы вынесли за скобку 2, а затем использовали формулу разности квадратов. Уж эту-то формулу нужно знать и видеть.

Рекомендация: Если в пределе (практически любого типа) можно вынести число за скобку, то всегда это делаем.
Более того, такие числа целесообразно выносить за значок предела. Зачем? Да просто чтобы они не мешались под ногами. Главное, потом эти числа не потерять по ходу решения.

Обратите внимание, что на заключительном этапе решения я вынес за значок предела двойку, а затем – минус.

Вообще, я заметил, что чаще всего в нахождении пределов данного типа приходится решать два квадратных уравнения, то есть и в числителе и в знаменателе находятся квадратные трехчлены.

Метод умножения числителя и знаменателя на сопряженное выражение

Продолжаем рассматривать неопределенность вида

Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас добавятся корни.

Сначала пробуем подставить 3 в выражение под знаком предела
Еще раз повторяю – это первое, что нужно выполнять для ЛЮБОГО предела. Данное действие обычно проводится мысленно или на черновике.

Получена неопределенность вида , которую нужно устранять.

Как Вы, наверное, заметили, у нас в числителе находится разность корней. А от корней в математике принято, по возможности, избавляться. Зачем? А без них жизнь проще.

Когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности используют метод умножения числителя и знаменателя на сопряженное выражение.

Вспоминаем нашу нетленную формулу разности квадратов:
И смотрим на наш предел:
Что можно сказать? у нас в числителе уже есть. Теперь для применения формулы осталось организовать (которое и называется сопряженным выражением).

Умножаем числитель на сопряженное выражение:

Обратите внимание, что под корнями при этой операции мы ничего не трогаем.

Хорошо, мы организовали, но выражение-то под знаком предела изменилось! А для того, чтобы оно не менялось, нужно его разделить на то же самое, т.е. на :

То есть, мы умножили числитель и знаменатель на сопряженное выражение.
В известной степени, это искусственный прием.

Умножили. Теперь самое время применить вверху формулу :

Неопределенность не пропала (попробуйте подставить тройку), да и корни тоже не исчезли. Но с суммой корней всё значительно проще, ее можно превратить в постоянное число. Как это сделать? Да просто подставить тройку под корни:

Число, как уже отмечалось ранее, лучше вынести за значок предела.

Как должно выглядеть решение данного примера в чистовом варианте?
Примерно так:

Умножим числитель и знаменатель на сопряженное выражение.

Сначала попробуйте решить его самостоятельно.

Окончательное решение примера может выглядеть так:

Разложим числитель на множители:

Умножим числитель и знаменатель на сопряженное выражение

Спасибо за внимание.

Автор: Емелин Александр

(Переход на главную страницу)

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

Определение непрерывности функции в точке и передела функции на бесконечности и на использовании свойств предела непрерывной функции способствует непосредственному вычислению пределов.

Значение предела в точке непрерывности определено значением функции в этой точке.

При опоре на свойства основные элементарные функции имеют предел в любой точке из области определения, вычисляется как значение соответствующей функции в этих точках.

Произвести вычисление предела функции lim x → 5 a r c t g 3 5 · x

Функция арктангенса отличается непрерывностью на всей своей области определения. Отсюда получим, что в точке x 0 = 5 функция является непрерывной. Из определения имеем, что для нахождения предела является значением этой же функции. Тогда необходимо произвести подстановку. Получим, что

lim x → 5 a r c t g 3 5 · x = a r c t g 3 5 · 5 = a r c t g 3 = π 3

Для вычисления односторонних пределов необходимо использовать значения точек границ предела. У акрксинуса и акрккосинуса имеются такие значения x 0 = - 1 или x 0 = 1 .

При x → + ∞ или x → - ∞ вычисляются пределы функции, заданные на бесконечностях.

Для упрощения выражений применяют свойства пределов:

lim x → x 0 ( k · f ( x ) ) = k · lim x → x 0 f ( x ) , k является коэффициентом.
lim x → x 0 ( f ( x ) · g ( x ) ) = lim x → x 0 f ( x ) · lim x → x 0 g ( x ) , применяемое при получении неопределенности предела.
lim x → x 0 ( f ( g ( x ) ) ) = f lim x → x 0 g x ,используемое для непрерывных функций, где знак функции и предельного перехода можно менять местами.

Для того, чтобы научиться вычислять переделы, необходимо знать и разбираться в основных элементарных функциях. Ниже приведена таблица, в которой имеются переделы этих функций с приведенными разъяснениями и подробным решением. Для вычисления необходимо основываться на определении предела функции в точке и на бесконечности.

Таблица пределов функции

Для упрощения и решения пределов используется данная таблица основных пределов.

Функция корень n-ой степени

y = x n , где n = 2 , 4 , 6 . . .

lim x → ∞ x n = + ∞ n = + ∞

Для любых x 0 из опрелеления

lim x → x 0 x n = x 0 n

Функция корень n-ой степени

y = x n , где n = 3 , 5 , 7 . . .

lim x → ∞ x n = + ∞ n = + ∞ lim x → ∞ x n = - ∞ n = - ∞

lim x → x 0 x n = x 0 n

Степенная функция y = x a , a > 0

Для любого положительного числа a
lim x → ∞ x a = + ∞ a = + ∞
Если a = 2 , 4 , 6 . . . , то
lim x → ∞ x a = - ∞ a = + ∞
Если a = 1 , 3 , 5 , . . . , то
lim x → ∞ x a = - ∞ a = - ∞
Для любых x 0 , из области определния
lim x → x 0 x a = ( x 0 ) a

Степенная функция y = x a , a 0

Для любого отрицательного числа a
lim x → ∞ x a = ( + ∞ ) a = + 0 lim x → 0 + 0 = ( 0 + 0 ) a = + ∞
Если a = - 2 , - 4 , - 4 , . . . , то
lim x → ∞ x a = - ∞ a = + 0 lim x → 0 - 0 x a = ( 0 - 0 ) a = + ∞
Если a = - 1 , - 3 , - 5 , . . . , то
lim x → ∞ x a = - ∞ a = - 0 lim x → 0 - 0 x a = ( 0 - 0 ) a = - ∞
Для любых x 0 из области определения
lim x → x 0 x a = ( x 0 ) a

Показательная функия

y = a x , 0 a 1

lim x → ∞ a x = a - ∞ = + ∞ lim x → ∞ a x = a + ∞ = + 0

Для любых x 0 из области опреления lim x → x 0 a x = a x 0

Показательная функия

y = a x , a > 1 lim x → ∞ a x = a - ∞ = + 0 lim x → x 0 a x = a + ∞ = + ∞

Для любых знвчений x 0 из област опредения lim x → x 0 a x = a x 0

Логарифмическая функция

y = log a ( x ) , 0 a 1

lim x → 0 + 0 log a x = log a ( 0 + 0 ) = + ∞ lim x → ∞ log a x = log a ( + ∞ ) = - ∞

Для любых x 0 из области опрелеления lim x → x 0 log a x = log a x 0

Логарифмическая функция

y = log a ( x ) , a > 1

lim x → 0 + 0 log a x = log a ( 0 + 0 ) = - ∞ lim x → ∞ log a x = log a ( + ∞ ) = + ∞

Для любых x 0 из области опрелеления

lim x → x 0 log a x = log a x 0

Тригонометрические функции

Синус
lim x → ∞ sin x не существует
Для любых x 0 из области опрелеления
lim x → x 0 sin x = sin x 0
Тангненс lim x → π 2 - 0 + π · k t g x = t g π 2 - 0 + π · k = + ∞ lim x → π 2 + 0 + π · k t g x = t g π 2 + 0 + π · k = - ∞

lim x → ∞ t g x не существует

Для любых x 0 из области опрелеления

lim x → x 0 t g x = t g x 0

Тригонометрические функции

Косинус
lim x → ∞ cos x не существует
Для любых x 0 из области опрелеления
lim x → x 0 cos x = cos x 0
Котангенс lim x → - 0 + π · k c t g x = c t g ( - 0 + π · k ) = - ∞ lim x → + 0 + π · k ctg x = ctg ( + 0 + π · k ) = + ∞

lim x → ∞ c t g x не существует

Для любых x 0 из области опрелеления
lim x → x 0 с t g x = с t g x 0

Обратные тригонометрические функции

Арксинус
lim x → - 1 + 0 a r c sin x = - π 2 lim x → 1 - 0 a r c sin x = π 2

Для любых x 0 из области опрелеления

lim x → x 0 a r c sin x = a r c sin x 0

Арккосинус
lim x → - 1 + 0 a r c cos ( x ) = π lim x → 1 - 0 arccos ( x ) = 0

Для любых x 0 из области опрелеления

lim x → x 0 a r c c i s x = a r c cos x 0

Обратные тригонометрические функции

Арктангес
lim x → - ∞ a r c t g ( x ) = - π 2 lim x → + ∞ a r c t g ( x ) = π 2

Для любых x 0 из области опрелеления

lim x → x 0 a r c t g x = a r c t g x 0

Арккотангенс
lim x → - ∞ a r c c t g ( x ) = π lim x → + ∞ a r c c t g ( x ) = 0

Для любых x 0 из области опрелеления

lim x → x 0 a r c c t g x = a r c c t g x 0

Произвести вычисление предела lim x → 1 x 3 + 3 x - 1 x 5 + 3 .

Для решения необходимо подставить значение х = 1 . Получаем, что

lim x → 1 x 3 + 3 x - 1 x 5 + 3 = 1 3 + 3 · 1 - 1 1 5 + 3 = 3 4 = 3 2

Ответ: lim x → 1 x 3 + 3 x - 1 x 5 + 3 = 3 2

Произвести вычисление предела функции lim x → 0 ( x 2 + 2 , 5 ) 1 x 2

Для того, чтобы раскрыть предел, необходимо подставить значение х, к которому стремится предел функции. В данном случае нужно произвести подстановку х = 0 . Подставляем числовое значение и получаем:

x 2 + 2 . 5 x = 0 = 0 2 + 2 . 5 = 2 . 5

Предел записывается в виде lim x → 0 ( x 2 + 2 . 5 ) 1 x 2 = lim x → 0 2 . 5 1 x 2 . Далее необходимо заняться значением показателя. Он является степенной функцией 1 x 2 = x - 2 . В таблице пределов, предоставленной выше, имеем, что lim x → 0 + 0 1 x 2 = lim x → 0 + 0 x - 2 = + ∞ и lim x → 0 + 0 1 x 2 = lim x → 0 + 0 x - 2 = + ∞ , значит, имеем право записать как lim x → 0 1 x 2 = lim x → 0 x - 2 = + ∞

Теперь вычислим предел. Получит вид lim x → 0 ( x 2 + 2 . 5 ) 1 x 2 = lim x → 0 2 . 5 1 x 2 = 2 . 5 + ∞

По таблице пределов с показательными функциями, имеющими основание больше 1 получаем, что

lim x → 0 ( x 2 + 2 . 5 ) 1 x 2 = lim x → 0 2 . 5 1 x 2 2 . 5 + ∞ = + ∞

Ответ: lim x → 0 ( x 2 + 2 . 5 ) 1 x 2 = + ∞

Когда задан более сложный предел, то при помощи таблицы не всегда получится получать целое или конкретное значение. Чаще получаются разные виды неопределенностей, для разрешения которых необходимо применять правила.

Рассмотрим графическое разъяснение приведенной выше таблицы пределов основных элементарных функций.

Предел константы

Из рисунка видно, что функция у = С имеет предел на бесконечности. Такой же предел при аргументе, который стремится к х 0 . Он равняется числу C .

Предел функции корень n-ой степени

Четные показатели корня применимы для lim x → + ∞ x n = + ∞ n = + ∞ , а нечетные, равные больше, чем значение 1 , – для lim x → + ∞ x n = + ∞ n = + ∞ , lim x → - ∞ x n = - ∞ n = - ∞ . Область определения может принимать абсолютно любое значение х предела заданной функции корня n -ой степени, равного значению функции в заданной точке.

Предел степенной функции

Необходимо разделить все степенные функции по группам, где имеются одинаковые значения пределов, исходя из показателя степени.

Когда a является положительным числом, тогда lim x → + ∞ x a = + ∞ a = + ∞ и lim x → - ∞ x a = - ∞ a = - ∞ . Когда x принимает любое значение, тогда предел степенной функции равняется значению функции в точке. Иначе это записывается как lim x → ∞ x a = ( ∞ ) a = ∞ .

Когда a является положительным четным числом, тогда получаем lim x → + ∞ x a = ( + ∞ ) a = + ∞ и lim x → - ∞ x a = ( - ∞ ) a = + ∞ , причем x из данной области определения является пределом степенной функции и равняется значением функции в этой точке. Предел имеет вид lim x → ∞ x a = ∞ a = + ∞ .

Когда a имеет другие значения, тогда lim x → + ∞ x a = ( + ∞ ) a = + ∞ , а область определения x способствует определению предела функции в заданной точке.

Когда a имеет значение отрицательных чисел, тогда получаем lim x → + ∞ x a = + ∞ a = + 0 , lim x → - ∞ x a = ( - ∞ ) a = - 0 , lim x → 0 - 0 x a = ( 0 - 0 ) a = - ∞ , lim x → 0 + 0 x a = 0 + 0 a = + ∞ , а значения x может быть любым из заданной области определения и равняется функции в заданной точке. Получаем, что lim x → ∞ x a = ∞ a = 0 и lim x → 0 x a = 0 a = ∞ .

Когда a является отрицательным четным числом, тогда получаем lim x → + ∞ x a = ( + ∞ ) a = + 0 , lim x → - ∞ x a = - ∞ a = + 0 , lim x → 0 - 0 ( 0 - 0 ) a = + ∞ , lim x → 0 + 0 x a = ( 0 + 0 ) a = + ∞ , а любое значение x на области определения дает результат предела степенной функции равным значению функции в точке. Запишем как lim x → ∞ x a = ( ∞ ) a = + 0 и lim x → 0 x a = ( 0 ) a = + ∞ .

Когда значение a имеет другие действительные отрицательные числа, тогда получим lim x → + ∞ x a = + ∞ a = + 0 и lim x → 0 + 0 x a = 0 + 0 a = + ∞ , когда x принимает любое значение из своей области определения, тогда предел степенной функции равняется значению функции в этой точке.

Предел показательной функции

Когда 0 a 1 , имеем, что lim x → - ∞ a x = a - ∞ = + ∞ , lim x → + ∞ a x = ( a ) + ∞ = + ∞ , любое значение x из области определения дает пределу показательной функции значению функции в точке.

Когда a > 1 , тогда lim x → - ∞ a x = ( a ) - ∞ = + 0 , lim x → + ∞ a x = ( a ) + ∞ = + ∞ , а любое значение x из области определения дает предел функции равный значению этой функции в точке.

Предел логарифмической функции

Когда имеем 0 a 1 , тогда lim x → 0 + 0 log a x = log a ( 0 + 0 ) = + ∞ , lim x → + ∞ log a x = log a ( + ∞ ) = - ∞ , для всех остальных значений x из заданной области определения предел показательной функции равняется значению заданной функции в точках.

Когда a > 1 , получаем lim x → 0 + 0 log a x = log a ( 0 + 0 ) = - ∞ , lim x → + ∞ log a x = log a ( + ∞ ) = + ∞ ,остальные значения x в заданной области определения дают решение предела показательной функции равному ее значению в точках.

Предел тригонометрических функций

Предел бесконечности не существует для таких функций как y = sin x , y = cos x . Любое значение x , входящее в область определения, равняется значению функции в точке.

Функция тангенса имеет предел вида lim x → π 2 - 0 + π · k t g ( x ) = + ∞ , lim x → π 2 + π · k t g ( x ) = ∞ или lim x → π 2 + π · k t g ( x ) = ∞ , тогда остальные значения x , принадлежащие области определения тангенса, равняется значению функции в этих точках.

Для функции y = c t g x получаем lim x → - 0 + π · k c t g ( x ) = - ∞ , lim x → + 0 + π · k c t g ( x ) = + ∞ или lim x → π · k c t g ( x ) = ∞ , тогда остальные значения x , принадлежащие области определения, дают предел котангенса, равный значению функции в этих точках.

Предел обратных тригонометрических функций

Функция арксинус имеет предел вида lim x → - 1 + 0 a r c sin ( x ) = - π 2 и lim x → 1 - 0 a r c sin ( x ) = π 2 , остальные значения x из области определения равняются значению функции в заданной точке.

Функция арккосинус имеет предел вида lim x → - 1 + 0 a r c cos ( x ) = π и lim x → 1 - 0 a r c cos ( x ) = 0 , когда остальные значения x , принадлежащие области определения, имеют предел арккосинуса, равного значению функции в этой точке.

Функция арктангенс имеет предел вида lim x → - ∞ a r c t g ( x ) = - π 2 и lim x → + ∞ a r c t g ( x ) = π 2 , причем другие значения x , входящие в область определения, равняется значению функции в имеющихся точках.

Функция котангенса имеет предел вида lim x → - ∞ a r c c t g ( x ) = π и lim x → + ∞ a r c t g ( x ) = 0 , где x принимает любое значение из своей заданной области определения, где получаем предел арккотангенса, равного значению функции в имеющихся точках.

Все имеющееся значения пределов применяются в решении для нахождения предела любой из элементарных функций.

Таблица пределов. Таблица пределов функций, формулы. Версия для печати.

Основные правила вычисления пределов.

Примечательные пределы:

Значимые специальные пределы:

Пределы простейших функций:

Пределы логарифмических и степенных функций:

Пределы тригонометрических функций:

Пределы при стремлении переменной к бесконечности:

Дополнительная информация от Инженерного cправочника DPVA, а именно - другие подразделы данного раздела:

Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.

В ряде разделов нашего справочника, где требуется применение понятия предела функции , встречаются несколько ситуаций в зависимости от того, куда стремится аргумент функции x , и того, куда при этом стремится значение функции. Определения предела функции для этих случаев удобно представить в форме таблицы. Однако таблица, описывающая все возможные случаи, должна содержать 24 строки и является слишком громоздкой. Для удобства читателей мы привели в таблице только те определения предела функции, которые использованы в нашем справочнике.

Предел функции f (x) при x, стремящемся к числу a, равен числу A

Число A называют пределом функции f (x) при x, стремящемся к числу a, если для любого положительного числа ε найдется такое положительное число δ , что при всех , удовлетворяющих неравенству

Предел функции f (x) при x, стремящемся к , равен числу A

Число A называют пределом функции f (x) при x , стремящемся к , если для любого положительного числа ε найдется такое положительное число С, что при всех x, удовлетворяющих неравенству

будет выполняться неравенство

| f (x) – A | f (x) при x, стремящемся к , равен числу A

Число A называют пределом функции f (x) при x , стремящемся к , если для любого положительного числа ε найдется такое отрицательное число С, что при всех x, удовлетворяющих неравенству

x f (x) при x, стремящемся к , равен числу A

будет выполняться неравенство

Предел функции f (x) при x, стремящемся к , равен

Функция f (x) стремится к при x, стремящемся к , если для любого положительного числа D найдется такое положительное число С, что при всех x, удовлетворяющих неравенству

будет выполняться неравенство

Предел функции f (x) при x, стремящемся к , равен

будет выполняться неравенство

Предел функции f (x) при x, стремящемся к , равен

Функция f (x) стремится к при x, стремящемся к , если для любого положительного числа D найдется такое отрицательное число С, что при всех x, удовлетворяющих неравенству

Предел функции f (x) при x, стремящемся к числу a слева, равен

Замечание . Когда говорят, что x стремится к a слева, то это означает, что при определении предела функции рассматриваются только те значения x , которые меньше a .

Функция f (x) стремится к , при x, стремящемся к числу a слева , если для любого положительного числа С найдется такое положительное число δ что при всех x, удовлетворяющих неравенству

Предел функции f (x) при x, стремящемся к числу a справа, равен

Замечание . Когда говорят, что x стремится к a справа, то это означает, что при определении предела функции рассматриваются только те значения x , которые больше a .

Функция f (x) стремится к , при x , стремящемся к числу a справа , если для любого положительного числа С, найдется такое положительное число δ что при всех x, удовлетворяющих неравенству

Предел функции f (x) при x, стремящемся к числу a, равен числу A

| x – a | f (x) при x, стремящемся к , равен числу A

будет выполняться неравенство

| f (x) – A | f (x) при x, стремящемся к , равен числу A

x f (x) при x, стремящемся к , равен числу A

будет выполняться неравенство

Предел функции f (x) при x, стремящемся к , равен

будет выполняться неравенство

Предел функции f (x) при x, стремящемся к , равен

Предел функции f (x) при x, стремящемся к числу a слева, равен

Предел функции f (x) при x, стремящемся к числу a справа, равен

Свойства пределов функций

Если у функций f (x) и g (x) при x , стремящемся к a , существуют пределы

где A и B – некоторые числа, то при x , стремящемся к a , существуют также и пределы суммы, разности и произведения этих функций , причем

Если, кроме того, выполнено условие

то при x , стремящемся к a , существует предел дроби

Для любой непрерывной функции F (x) справедливо равенство

Раскрытие неопределенностей типа

Определение 1 . Если при нахождении предела дроби выясняется, что и числитель дроби, и знаменатель дроби стремятся к стремятся к , то вычисление такого предела называют раскрытием неопределенности типа .

Решение . Преобразуем выражение, стоящее под знаком предела, к более удобному виду:

Раскрытие неопределенностей типа

Определение 2 . Если при нахождении предела дроби выясняется, что пределы числителя и знаменателя дроби равны 0 , то вычисление такого предела называют раскрытием неопределенности .

В алгебраических дробях неопределенность при x → a раскрывается при помощи разложения на множители числителя и знаменателя дроби с последующим сокращением на соответствующую степень множителя (x – a) .

Теперь предел знаменателя дроби равен – 11 , и, воспользовавшись свойствами пределов функций, получаем

Решение . В этом примере также возникает неопределенность типа .

Разложим теперь квадратный трехчлен 4x 2 – 9x – 55 на множители, а затем сократим числитель и знаменатель на (x – 5) :

К сожалению, из-за большого размера формул для расчета подробные вычисления на Вашем мобильном устройстве не видны. Их можно посмотреть только на устройствах с разрешением экрана по ширине не менее 768 пикселей (например, на стационарных компьютерах, ноутбуках и некоторых планшетах).

После этого, воспользовавшись свойствами пределов функций, получить ответ.

На Вашем мобильном устройстве отображается только результат описанных операций.

Первый замечательный предел

В пределах, содержащих тригонометрические функции, неопределенность раскрывается с помощью первого замечательного предела

Решение . Чтобы вычислить данный предел, перейдем от переменной x к новой переменной z по формуле

то предел можно преобразовать к виду

Раскрытие неопределенности типа . Второй замечательный предел

Определение 3 . Если при нахождении предела степени некоторого выражения выясняется, что предел основания степени равен 1, а предел показателя степени равен , то вычисление такого предела называют раскрытием неопределенности .

Неопределенность раскрывается с помощью второго замечательного предела :

Если взять натуральный логарифм от обеих частей формулы (1), то второй замечательный предел примет вид:

Решение . Рассмотрим функцию

и, взяв от нее натуральный логарифм, найдем сначала предел функции y = ln f (x) при x → . Применяя свойства логарифмов, получаем

Преобразуем выражение, стоящее под знаком логарифма к виду, удобному для применения второго замечательного предела,

Поэтому функцию y = ln f (x) удобно представить в сдедующем виде

Следовательно, воспользовавшись свойствами пределов функций, получаем

Решение . Рассмотрим функцию

и, взяв от нее натуральный логарифм, найдем сначала предел функции y = ln f (x) при x → – 6 . Применяя свойства логарифмов, получаем

Чтобы вычислить предел функции y = ln f (x) при x → – 6 , перейдем от переменной x к новой переменной z по формуле

то предел (3) можно преобразовать к виду , с помощью формулы (3), получаем

Читайте также: