Симплексный метод решения задачи линейного программирования кратко
Обновлено: 05.07.2024
Симплекс-метод - это итеративный процесс направленного решения системы уравнений по шагам, который начинается с опорного решения и в поисках лучшего варианта движется по угловым точкам области допустимого решения, улучшающих значение целевой функции до тех пор, пока целевая функция не достигнет оптимального значения.
. Алгоритм симплекс-метода
Пример 5.1. Решить следующую задачу линейного программирования симплекс-методом:
Решение:
I итерация:
1 этап: формирование исходной симплекс-таблицы.
Исходная задача линейного программирования задана в стандартной форме. Приведем ее к каноническому виду путем введения в каждое из ограничений-неравенств дополнительной неотрицательной переменной, т.е.
В полученной системе уравнений примем в качестве разрешенных (базисных) переменные х3, х4, х5, х6, тогда свободными переменными будут х1,х2. Выразим базисные переменные через свободные:
Приведем целевую функцию к следующему виду:
На основе полученной задачи сформируем исходную симплекс-таблицу:
Таблица 5.3
Исходная симплекс-таблица
2 этап: определение базисного решения.
Согласно определению базисного решения свободные переменные равны нулю, а значения базисных переменных – соответствующим значениям свободных чисел, т.е.:
3 этап: проверка совместности системы ограничений ЗЛП.
На данной итерации (в таблице 5.3) признак несовместности системы ограничений (признак 1) не выявлен (т.е. нет строки с отрицательным свободным числом (кроме строки целевой функции), в которой не было бы хотя бы одного отрицательного элемента (т.е. отрицательного коэффициента при свободной переменной)).
4 этап: проверка ограниченности целевой функции.
На данной итерации (в таблице 5.3) признак неограниченности целевой функции (признак 2) не выявлен (т.е. нет колонки с отрицательным элементом в строке целевой функции (кроме колонки свободных чисел), в которой не было бы хотя бы одного положительного элемента).
5 этап: проверка допустимости найденного базисного решения.
Так как найденное базисное решение не содержит отрицательных компонент, то оно является допустимым.
6 этап: проверка оптимальности.
Найденное базисное решение не является оптимальным, так как согласно признаку оптимальности (признак 4) в строке целевой функции не должно быть отрицательных элементов (свободное число данной строки при рассмотрении данного признака не учитывается). Следовательно, согласно алгоритму симплекс-метода переходим к 8 этапу.
8 этап: определение разрешающего элемента.
8.1. Определение разрешающей колонки.
8.2. Определение разрешающей строки.
Для определения разрешающей строки находим положительные оценочные отношения свободных чисел к элементам разрешающей колонки, строка, которой соответствует наименьшее положительное оценочное отношение, принимается в качестве разрешенной.
Таблица 5.4
Исходная симплекс-таблица
9 этап: преобразование симплекс-таблицы.
9.1. Преобразование разрешающего элемента.
Разрешающий элемент таблицы 5.4 преобразовывается следующим образом:
Полученный результат вписываем в аналогичную клетку таблицы 5.5.
9.2. Преобразование разрешающей строки.
Элементы разрешающей строки таблицы 5.4 делим на разрешающий элемент данной симплекс-таблицы, результаты вписываются в аналогичные ячейки новой симплекс-таблицы (таблицы 5.5). Преобразования элементов разрешающей строки приведены в таблице 5.5.
9.3. Преобразование разрешающей колонки.
Элементы разрешающей колонки таблицы 5.4 делим на разрешающий элемент данной симплекс-таблицы, а результат берется с обратным знаком. Полученные результаты вписываются в аналогичные ячейки новой симплекс-таблицы (таблицы 5.5). Преобразования элементов разрешающей колонки приведены в таблице 5.5.
9.4. Преобразование остальных элементов симплекс-таблицы.
Аналогично преобразуются значения других клеток:
В результате данных преобразований получили новую симплекс- таблицу (таблица 5.5).
II итерация:
1 этап: составление симплекс-таблицы.
По результатам симплекс-преобразований предыдущей итерации составляем новую симплекс-таблицу:
Таблица 5.5
Симплекс-таблица II итерации
Симплексный метод линейного программирования относится к универсальным методам, обеспечивающим эффективное решение разнообразных землеустроительных и других экономических задач. Универсальность данного метода проявляется в том, что он позволяет решать задачи различной размерности, в которых технико-экономические коэффициенты (αij) при переменных (Хij) выражены в разных единицах измерения.
Сущность симплексного метода заключается в нахождении оптимального решения задачи путем последовательного рассмотрения и анализа ее допустимых базисных решений. Геометрически каждое допустимое базисное решение соответствует одной из вершин многоугольника в n–мерном пространстве ограничивающего в соответствии с условиями задачи область допустимых решений (ОДР).
В процессе решения задачи на каждой итерации осуществляется переход из одной вершины ОДР в смежную, связанную с не худшим значением целевой функции. Для этого используется процедура метода главных элементов. Количество итераций, необходимых для получения оптимального решения, находится в пределах от m до 2m, где m-количество ограничений в задаче.
Экономико-математические модели задач линейного программирования, решаемых симплексным методом, могут быть представлены в структурной форме или в развернутом виде. Структурная модель задачи записывается следующим образом:
при условиях: /i=1,2,…m/ (3.2)
Если подробно описать все условия задачи в виде системы неравенств и уравнений, то такая экономико-математическая модель называется развернутой.
В зависимости от сложности решаемых задач экономико-математические модели могут иметь разные размеры, которые определяются произведением количества ограничений на количество переменных (m∙n).
3.1 РЕШЕНИЕ ЗАДАЧ ПРОГРАММИРОВАНИЯ СИМПЛЕКСНЫМ МЕТОДОМ
Экономико-математические модели линейного программирования структурно состоят из трех частей: целевой функции, системы ограничений и условия не отрицательности переменных. Целевая функция выражает основное условие задачи, критерий её оптимальности, ориентированный на максимум или на минимум.
Система ограничений в экономико-математических моделях задач, решаемых симплексным методом, записывается в стандартной форме, т.е. в виде неравенств и уравнений. В зависимости от типа ограничений задачи решаются по алгоритму симплексного метода, или алгоритму данного метода с искусственным базисом.
Рассмотрим алгоритм решения задач симплексным методом, который применяется и при решении задач с искусственным базисом за исключением некоторых особенностей алгоритма на начальных этапах их решения.
Методика решения задач симплексным методом предусматривает соблюдение следующих этапов их решения:
1. Постановка задачи;
2. Составление экономико-математические модели задачи;
3. Составление исходного плана (первой симплексной таблицы);
4. Анализ плана на оптимальность;
5. Улучшение плана;
6. Контроль правильности решения задачи;
7. Анализ оптимального решения задачи и формулирование ответа.
Для более наглядного представления алгоритма симплексного метода решим задачу, выраженную в условных единицах измерения.
1. Постановка задачи
При постановке задачи формулируется (словесно): оптимальные значения, каких неизвестных необходимо найти, при каких условиях (ограничениях) по видам и размерам ресурсов, какая функция цели и на что она ориентирована (на максимум или минимум). Например, необходимо определить оптимальное сочетание объемов производства трех видов продукции (Х1, Х2, Х3) при имеющихся в хозяйстве трех видах ресурсов в размере в1=100, в2=40, в3=50 (это могут быть трудовые ресурсы, удобрения, капиталовложения и т.п.) с целью получения максимальной денежной выручки (или валовой продукции и т.п.).
2. Составление экономико-математические модели задачи
Экономико-математическая модель в симплексном методе составляется в следующей последовательности:
- записывается уравнение функции цели, правая часть которого представляет собой сумму произведений искомых неизвестных (Х1, Х2, Х3) на соответствующие им по условиям задачи коэффициенты целевой функции:

- условия задачи записываются в виде неравенств с ограничениями типа ≤. Каждое из неравенств выражает собой ограничения по одному из видов ресурсов, поэтому в левой части неравенства проставляют искомые переменные с коэффициентами, выражающими расход данного вида ресурса на единицу искомой переменной или, наоборот, выход данного вида ресурса с единицы соответствующей переменной. В правой части неравенства проставляется тип ограничения ≤ и величина соответствующего вида ресурса;
- количество неравенств в системе ограничений обусловлено условиями задачи. При записи неравенств необходимо контролировать правильность их оформления: технико-экономические коэффициенты при переменных, состав переменных (в левой части неравенства), вид и размер ресурса (в правой части неравенства) должны строго соответствовать условиям задачи и характеру её постановки.
Таким образом, система ограничений выглядит следующим образом:
- после записи основных условий задачи в виде системы ограничений обязательно формулируется условие не отрицательности переменных, так как алгоритм симплексного метода позволяет решать задачи только с положительными значениями переменных (Хj):
Представленная выше форма записи условий задачи в виде неравенств называется стандартной. Для заполнения первой симплексной таблицы (исходного плана) необходимо перейти от стандартной формы записи условий задачи к канонической, а от неё – к симплексной.
Преобразуем приведенную выше систему неравенств в систему уравнений:
Для дальнейшего преобразования канонической формы записи в симплексную система уравнений решается относительно дополнительных переменных:
Исходя из симплексной формы записи условий задачи, становится ясен экономический смысл дополнительных переменных. На начальном этапе решения задачи принимается условие, что основные переменные равны нулю, а значения дополнительных переменных, исходя из симплексной формы записи, будут равны величинам ресурсов. В нашем примере: при Х1=0, Х2=0, Х3=0 будем иметь Х4=100, Х5=40, Х6=50.
В экономическом отношении это означает, что пока не реализовано ни одно из мероприятий, намечаемых по условиям задачи, ресурсы остаются неиспользованными. Исходя из данной установки, создается исходный базис (исходное условие), на основе которого начинается поиск оптимального решения задачи из числа допустимых её решений.
Если в системе уравнений отражающих условие задачи, количество переменных (n) больше количества ограничений (m), то система имеет множество решений. При этом допустимым решением системы называется любой набор переменных, удовлетворяющих условиям задачи, а допустимым базисным решением – допустимое решение, содержащее не больше, чем m не нулевых переменных. Поэтому первая симплексная таблица (исходный план) содержит допустимое базисное решение задачи. Рассмотрим порядок заполнения первой симплексной таблицы (таблица 3.1).
3. Составление исходного плана (первой симплексной таблицы)
Содержание первой симплексной таблицы и порядок её заполнения рассмотрим последовательно по столбцам и строкам.
Столбец 1 – приводится нумерация строк, соответствующая нумерации ограничений в задаче.
Столбец 2 – записывается только дополнительные переменные (Х4, Х5, Х6), т.к. они составляют исходный базис для начала решения задачи.
Столбец 3 – записываются коэффициенты целевой функции при дополнительных переменных, вошедших в базис. Они равны нулю, т.к. дополнительные переменные (Х4, Х5, Х6), вошедшие в базис, в целевую функцию введены с нулевыми коэффициентами (Сij =0) для исключения влияния дополнительных переменных на величину функции цели (Z).
Столбец 4 – записывается значение ресурсов (свободных членов), стоящих в правой части соответствующего неравенства (уравнения). Исходя из симплексной формы записи условий рассматриваемой задачи дополнительные переменные, вошедшие в базис, выражают неиспользованные ресурсы, поэтому: Х4=100, Х5=40, Х6=50. Следовательно, в столбец свободных членов (вj) записываются исходные величины ресурсов.
Столбцы 5-7 – это столбцы основных переменных (соответственно, Х1, Х2, Х3). В них на пересечении со строками соответствующих уравнений проставляются технико-экономические коэффициенты (аij), стоящие в данных уравнениях при каждой из основных переменных. Так, из первого уравнения (3.8) 3Х1+5Х2+8Х3+Х4=100 коэффициенты при основных переменных (Х1, Х2, Х3), соответственно 3,5 и 8 занесены в столбцы данных переменных по первой строке таблицы (3.1).
Столбец 11 – в него записывается суммы, полученные путем сложения свободного члена (вj) и коэффициентов (аij) по соответствующей строке таблицы. Так, если сложить по первой строке таблицы (3.1) свободный член и коэффициенты (100+3+5+8+1=117), то получим число 117, которое и записано в столбце 11. аналогичным образом получаем значения для столбца 11 и по остальным строкам таблицы.
Столбец 12 – в него записываются значения, полученные в результате построчного деления значений свободных членов (вj) на положительные коэффициенты ключевого (k-го) столбца.
Для выполнения таких расчетов необходимо предварительно выбрать ключевой столбец (k–й столбец). В качестве ключевого (k-го) выбирается столбец (из числа столбцов основных переменных Х1, Х2, Х3, т.е. столбцов 5-7), по которому в индексной (m+n) строке таблицы стоит максимальное по абсолютной величине: отрицательное число при решении задачи на максимум и, наоборот, положительное число, при решении задачи на минимум.
Теперь можно выполнить расчеты для заполнения столбца 12. По первой строке указанное отношение получаем, разделив свободный член 100 (в1=100) на положительный коэффициент 8 (в1=8), стоящий по данной строке в ключевом столбце. Оно равно 12,5 ( ). Запишем его в таблицу 3.1.
Аналогично определяем остальные значения для столбца 12.
Значения, записываемые в столбце 12 служат, в последующем основанием для выбора ключевой строки (l-строки), используемой вместе с ключевым (k-столбцом) столбцом для получения следующей симплексной таблицы (улучшенного плана).
Столбец m+1 – это индексная строка симплексной таблицы. На пересечении m+1 строки и столбца основных членов вi (столбец 4), записывается численное значение функции цели (Z). В первой симплексной таблице (3.1) оно равно нулю (Z=0).
Все остальные элементы индексной (m+1) строки рассчитываются по формуле:
где Сi – коэффициенты целевой функции при переменных, вошедших в базис;
Cj - коэффициенты целевой функции при переменных (Хij), по столбцам которых выполняется расчет;
аij – технико-экономические коэффициенты при переменных Хj, стоящих в i-м ограничении.
Так, для столбца переменной Х1 (столбец 3) элемент индексной строки будет рассчитан следующим образом:
Так же рассчитываются остальные элементы индексной строки (для столбцов 5-10). В столбец 11 проставляется сумма элементов по индексной строке (-60).
Заполненная первая симплексная таблица (3.1) представляет собой исходный план, который анализируется на оптимальность.
4. Анализ плана на оптимальность
Признаком оптимальности опорного (как исходного, так и последующих) плана является отсутствие в индексной (m+1) строке при решении задачи на минимум – положительных коэффициентов или нулей. Если это условие не выполняется, то план не оптимален и необходимо его улучшать.
В рассматриваемой задаче, решаемой на максимум, исходный план (таблица 3.1) не оптимален, т.к. в индексной строке имеются отрицательные коэффициенты (-20, -10, -30). В связи с этим его необходимо улучшать.
5. Улучшение плана
Новый, улучшенный план, получают на основе преобразования неоптимального плана. Вычислительная процедура улучшения плана заключается в выведении из базиса неоптимального плана одной из базисных переменных и введение в него новой, небазисной переменной. Для осуществления этой процедуры в неоптимальном (улучшаемом плане, т.е. в первой симплексной таблице) выбирают ключевой К-столбец и ключевую l-строку (таблица 3.1).
Ключевой столбец (К-столбец) выбирают, как было отмечено выше, по наибольшему по абсолютной величине: отрицательному коэффициенту индексной строки при решении задачи на максимум, и положительному коэффициенту при решении задачи на минимум.
В первой симплексной таблице (неоптимальном плане) в качестве ключевого нами выбран столбец переменной Х3 (столбец 7), в котором по индексной строке стоит наибольший по абсолютной величине отрицательный коэффициент -30 (Zmax).
Ключевая строка (l-строка) выбирается по минимальному положительному коэффициенту, стоящему в столбце 12. В первой симплексной таблице рассматриваемой задачи в качестве ключевой l-строки выбрана вторая строка, по которой в столбце 12 стоит наименьший положительный коэффициент (6,67).
Коэффициент, стоящий на пересечении ключевой строки и ключевого столбца называется главным или генеральным элементом (alk).
Новую симплексную таблицу (улучшенный план) с новым базисным решением составляют в следующей последовательности:
- вычерчивают новую симплексную таблицу (3.2) по форме первой таблицы, добавляя столбец 13 (для контроля правильности вычислений). Вместо базисной переменной, стоявшей в базисе (столбец 2) по ключевой l-строке предыдущей таблицы в новую таблицу записывают переменную Хj, столбец которой выбран в качестве ключевого. Этим самым в базис новой симплексной таблицы вводится новая базисная переменная, а прежняя – выводится из базиса;
- в столбец 3, рядом с новой переменной, введенной в базис, записывают её коэффициент целевой функции. Остальные базисные переменные и их коэффициенты целевой функции (столбцы 2 и 3) переписываются в новую таблицу из предыдущей без изменения;
- элементы ( ) для заполнения в новой таблице строки, стоящей на месте ключевой l-строки предыдущей таблицы, вычисляются как отношение соответствующего элемента (alj) ключевой l-строки на главный элемент (alk) предыдущей таблицы, т.е. по формуле:
, (3.15)
- элементы остальных строк новой симплексной таблицы, за исключением строки, стоящей на месте бывшей ключевой l-строки, пересчитываются по одной из следующих формул:
где , аij – однотипные коэффициенты, соответственно новой и предыдущей симплексной таблиц;
, аlj – коэффициенты строки, стоящей в новой таблице на месте бывшей ключевой l-строки и, соответственно, коэффициенты ключевой l-строки в предыдущей таблице;
aik – коэффициенты ключевого К-столбца предыдущей симплексной таблицы;
alk – главный (генеральный) элемент предыдущей симплексной таблицы, стоящий на пересечении ключевых l-строки и К-столбца.
Расчеты по указанным выше формулам выполняются для заполнения всех строк новой симплексной таблицы, включая индексную (m+1) строку, но исключая ключевую l-строку.
В соответствии с вышеизложенным выполнены расчеты по улучшению первого и второго планов (таблицы 3.1 и 3.2) и получен оптимальный план (таблица 3.3).
Данный онлайн калькулятор решает задачу линейного программирования симплекс методом. Дается подробное решение с пояснениями. Для решения задачи линейного программирования задайте количество ограничений и количество переменных. Затем введите данные в ячейки и нажимайте на кнопку "Вычислить". Теоретическую часть смотрите в статье: Решение задачи линейного программирования. Симплекс метод.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Симплекс метод
Симплекс метод − это метод решения задачи линейного программирования (ЗЛП). Суть метода заключается в нахождении начального допустимого плана, и в последующем улучшении плана до достижения максимального (или минимального) значения целевой функции в данном выпуклом многогранном множестве или выяснения неразрешимости задачи. Подробнее в статье: Решение задачи линейного программирования. Симплекс метод.
Примеры решения ЗЛП симплекс методом
Пример 1. Решить следующую задачу линейного программирования:
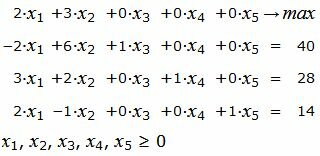 |
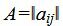
Р е ш е н и е. Матрица коэффициентов системы уравнений имеет вид:
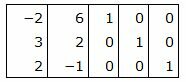 |
Правая часть ограничений системы уравнений имеет вид:
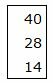 |
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последняя строка - это целевая функция, умноженная на −1. Последние три векторы столбцы обазуют базис в трехмерном пространствое. Следовательно базисные переменные , а свободные переменные :
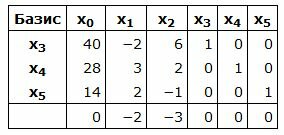 |
Запишем текущий опорный план:
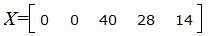 |
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-3), следовательно в базис входит вектор x2. Определяем, какой вектор выходит из базиса. Для этого вычисляем при . min(40:6, 28:2)=20/3 соответствует строке 1. Из базиса выходит вектор x3. Сделаем исключение Гаусса для столбца x2, учитывая, что ведущий элемент соответствует строке 1. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 2, 3, 4 со строкой 1, умноженной на -1/3, 1/6, 1/2, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
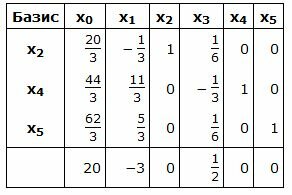 |
Запишем текущий опорный план:
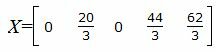 |
Данный опорный план не является оптимальным, так как в последней строке есть отрицательный элемент (-3), следовательно в базис входит вектор x1. Определяем, какой вектор выходит из базиса. Для этого вычисляем при . min(44/3:11/3, 62/3:5/3)=4 соответствует строке 2. Из базиса выходит вектор x4. Сделаем исключение Гаусса для столбца x1, учитывая, что ведущий элемент соответствует строке 2. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 1, 3, 4 со строкой 2, умноженной на 1/11, -5/11, 9/11, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
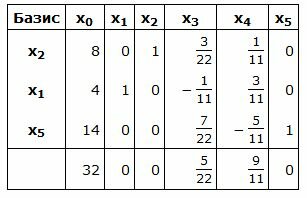 |
Запишем текущий опорный план:
 |
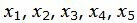
Текущий опорный план является оптимальным, так как в строках 4 под переменными нет отрицательных элементов.
Решение можно записать так: .
Значение целевой функции в данной точке: F(X)=.
Пример 2. Найти максимум функции
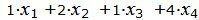 |
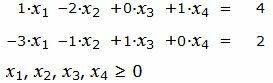 |
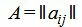
Р е ш е н и е. Матрица коэффициентов системы уравнений имеет вид:
 |
Правая часть ограничений системы уравнений имеет вид:
 |
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последняя строка - это целевая функция, умноженная на −1:
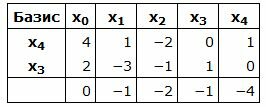 |
Базисные векторы x4, x3, следовательно, все элементы в столбцах x4, x3, ниже горизонтальной линии должны быть нулевыми.
Обнулим все элементы столбца x4, кроме ведущего элемента. Для этого сложим строку 3 со строкой 1, умноженной на 4. Обнулим все элементы столбца x3, кроме ведущего элемента. Для этого сложим строку 3 со строкой 2, умноженной на 1.
Симплекс таблица примет вид:
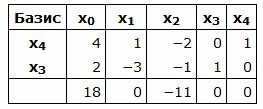 |
Запишем текущий опорный план:
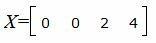 |
Данный опорный план не является оптимальным, так как в последней строке есть отрицательный элемент (-11), следовательно в базис входит вектор x2. Определяем, какой вектор выходит из базиса. Для этого вычисляем при . Все следовательно целевая функция неограничена сверху. Т.е. задача линейного программирования неразрешима.
Примеры решения ЗЛП методом искусственного базиса
Пример 1. Найти максимум функции
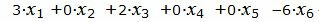 |
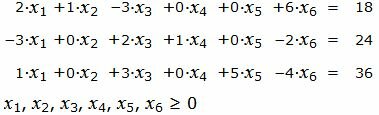 |
Р е ш е н и е. Так как количество базисных векторов должен быть 3, то добавляем искусственное переменное, а в целевую функцию добавляем это переменное, умноженное на −M, где M, очень большое число:
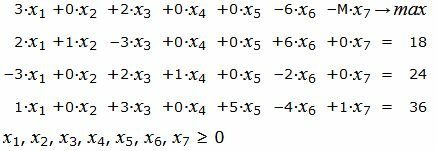 |
Матрица коэффициентов системы уравнений имеет вид:
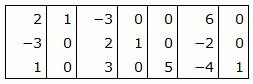 |
Правая часть ограничений системы уравнений имеет вид:
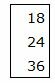 |
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последние две строки − это целевая функция, умноженная на −1 и разделенная на две части. Последняя строка − строка с исскуственными переменными:
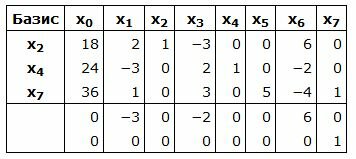 |
Базисные векторы следовательно, все элементы в столбцах ниже горизонтальной линии должны быть нулевыми.
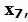
Обнулим все элементы столбца кроме ведущего элемента. Для этого сложим строку 5 со строкой 3, умноженной на -1.
Симплекс таблица примет вид:
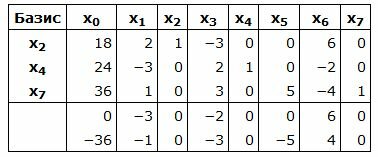 |
Запишем текущий опорный план:
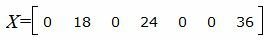 |
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-5), следовательно в базис входит вектор Определяем, какой вектор выходит из базиса. Для этого вычисляем при соответствует строке 3. Из базиса выходит вектор Сделаем исключение Гаусса для столбца учитывая, что ведущий элемент соответствует строке 3. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строку 5 со строкой 3, умноженной на 1. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
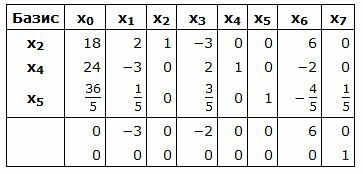 |
Запишем текущий опорный план:
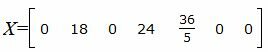 |
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-3), следовательно в базис входит вектор Определяем, какой вектор выходит из базиса. Для этого вычисляем при соответствует строке 1. Из базиса выходит вектор x2. Сделаем исключение Гаусса для столбца x1, учитывая, что ведущий элемент соответствует строке 1. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 2, 3, 4 со строкой 1, умноженной на 3/2, -1/10, 3/2, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
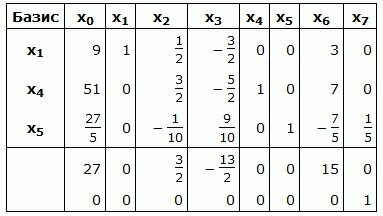 |
Запишем текущий опорный план:
 |
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-13/2), следовательно в базис входит вектор x3. Определяем, какой вектор выходит из базиса. Для этого вычисляем при соответствует строке 3. Из базиса выходит вектор x5. Сделаем исключение Гаусса для столбца x3, учитывая, что ведущий элемент соответствует строке 3. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 1, 2, 4 со строкой 3, умноженной на 5/3, 25/9, 65/9, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
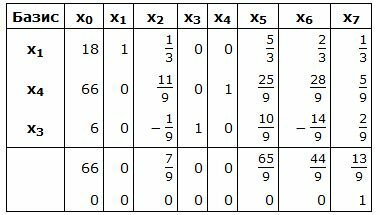 |
Запишем текущий опорный план:
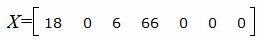 |
Текущий опорный план является оптимальным, так как в строках 4−5 под переменными нет отрицательных элементов.
Решение исходной задачи можно записать так:
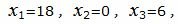 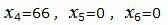 . |
Значение целевой функции в данной точке:
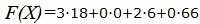 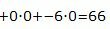 . |
Пример 2. Найти оптимальный план задачи линейного программирования:
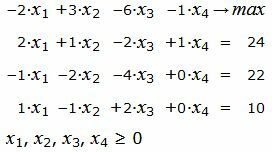 |
Р е ш е н и е. Так как количество базисных векторов должен быть 3, то добавляем искусственные переменные, а в целевую функцию добавляем эти переменные, умноженные на −M, где M, очень большое число:
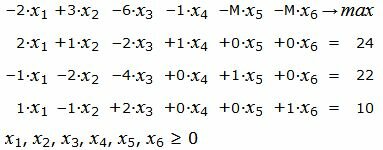 |
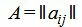
Матрица коэффициентов системы уравнений имеет вид:
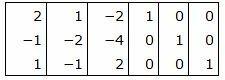 |
Правая часть ограничений системы уравнений имеет вид:
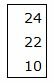 |
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последние две строки − это целевая функция, умноженная на −1 и разделенная на две части. Последняя строка − строка с исскуственными переменными:
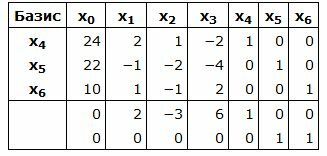 |
Базисные векторы x4, x5, x6, следовательно, все элементы в столбцах x4, x5, x6, ниже горизонтальной линии должны быть нулевыми.
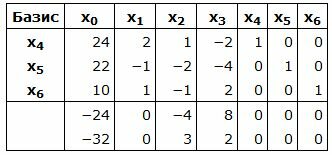
Обнулим все элементы столбца x4, кроме ведущего элемента. Для этого сложим строку 4 со строкой 1, умноженной на -1. Обнулим все элементы столбца x5, кроме ведущего элемента. Для этого сложим строку 5 со строкой 2, умноженной на -1. Обнулим все элементы столбца x6, кроме ведущего элемента. Для этого сложим строку 5 со строкой 3, умноженной на -1.
Симплекс таблица примет вид:
 |
Запишем текущий опорный план:
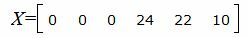 |
В строке 5 элементы, соответствующие переменным x1, x2, x3, x4, x5, x6 неотрицательны, а число находящийся в пересечении данной строки и столбца x0 отрицательнo. Тогда исходная задача не имеет опорного плана. Следовательно она неразрешима.
Если вы уже разобрались с графическим методом решения задач линейного программирования, самое время переходить к симплекс-методу. В отличие от первого, он практически не имеет ограничений на задачу (любое количество переменных, разные знаки и т.п.) и модифицируется в зависимости от типа задачи (например, М-метод или метод искусственного базиса).
При решении задачи симплекс методом вычисления обычно ведутся (для компактности и наглядности) в таблицах (табличный симплекс-метод), причем последняя таблица с оптимальным решением содержит важную дополнительную информацию: решение двойственной задачи, остатки ресурсов, сведения о дефицитных ресурсах и т.п., которая позволяет провести экономический анализ задачи линейного программирования (см. ниже пример 3).
Примеры решений задач симплекс-методом выложены бесплатно для вашего удобства - изучайте, ищите похожие, решайте. Если вам нужна помощь в выполнении подобных заданий, перейдите в раздел: решение линейного программирования на заказ.
Решение задач симплекс-методом: примеры онлайн
Задача 1. Компания производит полки для ванных комнат двух размеров - А и В. Агенты по продаже считают, что в неделю на рынке может быть реализовано до 550 полок. Для каждой полки типа А требуется 2 м2 материала, а для полки типа В - 3 м2 материала. Компания может получить до 1200 м2 материала в неделю. Для изготовления одной полки типа А требуется 12 мин машинного времени, а для изготовления одной полки типа В - 30 мин; машину можно использовать 160 час в неделю. Если прибыль от продажи полок типа А составляет 3 денежных единицы, а от полок типа В - 4 ден. ед., то сколько полок каждого типа следует выпускать в неделю?
Задача 2. Решить задачу линейного программирования симплекс-методом.
Задача 3. Предприятие производит 3 вида продукции: А1, А2, А3, используя сырьё двух типов. Известны затраты сырья каждого типа на единицу продукции, запасы сырья на планируемый период, а также прибыль от единицы продукции каждого вида.
- Сколько изделий каждого вида необходимо произвести, чтобы получить максимум прибыли?
- Определить статус каждого вида сырья и его удельную ценность.
- Определить максимальный интервал изменения запасов каждого вида сырья, в пределах которого структура оптимального плана, т.е. номенклатура выпуска, не изменится.
- Определить количество выпускаемой продукции и прибыль от выпуска при увеличении запаса одного из дефицитных видов сырья до максимально возможной (в пределах данной номенклатуры выпуска) величины.
- Определить интервалы изменения прибыли от единицы продукции каждого вида, при которых полученный оптимальный план не изменится.
Задача 4. Решить задачу линейного программирования симплексным методом:
Задача 5. Решить задачу линейного программирования симплекс-методом:
Задача 6. Решить задачу симплекс-методом, рассматривая в качестве начального опорного плана, план, приведенный в условии:
Задача 7. Решить задачу модифицированным симплекс-методом.
Для производства двух видов изделий А и Б используется три типа технологического оборудования. На производство единицы изделия А оборудование первого типа используется а1=4 часов, оборудование второго типа а2=8 часов, а оборудование третьего типа а3=9 часов. На производство единицы изделия Б оборудование первого типа используется б1=7 часов, оборудование второго типа б2=3 часов, а оборудование третьего типа б3=5 часов.
На изготовление этих изделий оборудование первого типа может работать не более чем t1=49 часов, оборудование второго типа не более чем t2=51 часов, оборудование третьего типа не более чем t3=45 часов.
Прибыль от реализации единицы готового изделия А составляет АЛЬФА=6 рублей, а изделия Б – БЕТТА=5 рублей.
Составить план производства изделий А и Б, обеспечивающий максимальную прибыль от их реализации.
Задача 8. Найти оптимальное решение двойственным симплекс-методом
Читайте также:

