Принцип независимости движения кратко
Обновлено: 14.05.2024
1.Механическое движение. Система отсчета. Тело отсчета. Материальная точка. Основные понятия кинематики. Траектория. Путь и перемещение. Мгновенная скорость. Ускорение. Относительность механического движения. Закон сложения скоростей.
2.Равноускоренное прямолинейное движение. Формулы зависимости скорости и координаты от времени при равноускоренном прямолинейном движении. Графики зависимости кинематических величин от времени при равномерном и равноускоренном движениях. Определение ускорения и перемещения по графику зависимости скорости от времени.
3.Свободное падение тел. Ускорение свободного падения. Движение тела брошен-ного вертикально вверх (вывод формул зависимости скорости и координаты от времени) . Движение тела брошенного горизонтально (вывод формул зависимо-сти скорости и координаты от времени) .
4.Принцип независимости движения. Движение тела брошенного под углом к горизонту (вывод формул зависимости скорости и координаты от времени) .
5.Движение материальной точки по окружности. Период и частота. Центростремительное ускорение. Тангенциальное ускорение. Полное ускорение. Угловая скорость. Связь угловой и линейной скорости. Угловое ускорение. Связь углового и линейного ускорения.
6.Условия движения тел без ускорения. Первый закон Ньютона. Инерция. Гра-ницы применимости первого закона Ньютона. Инерциальные системы отсчета. Принцип относительности Галилея.
7.Инертность тел. Масса. Сила. Принцип суперпозиции сил. Принцип независимости действия сил. Второй закон Ньютона. Границы применимости второго закона Ньютона.
8.Взаимодействие тел. Третий закон Ньютона. Характеристика сил взаимодейст-вия по модулю, направлению, точке приложения и природе этих сил. Границы применимости третьего закона Ньютона.
9.Гравитационное поле. Закон всемирного тяготения. Физический смысл гравитационной постоянной. Сила тяжести. Центр тяжести. Расчёт первой космической скорости (вывод формулы) . Ускорение свободного падения как силовая характеристика гравитационного поля (вывод формулы) .
10. Вес тела. Вес тела, движущегося с ускорением направленным вертикально вверх (вывод формулы) . Перегрузки. Вес тела, движущегося с ускорением направленным вертикально вниз (вывод формулы) . Невесомость.
11. Деформация тел. Причины деформации тел. Виды деформации. Силы упругости. Природа сил упругости. Напряжения. Абсолютное и относительное удлинение. Закон Гука. Модуль Юнга. Коэффициент жёсткости. Диаграмма напряжений. Границы применимости закона Гука.
12. Силы трения. Природа сил трения. Коэффициент трения скольжения. Закон сухого трения. Учёт и использование трения в быту и технике.
13. Импульс тела. Выражение второго закона Ньютона через изменение импульса тела и импульс силы (вывод формулы) . Закон сохранения импульса. Границы применимости закона сохранения импульса. Проявление закона сохранения импульса в природе и его использование в технике.
14. Механическая энергия. Кинетическая энергия (вывод формулы) . Потенциальная энергия тела поднятого над поверхностью земли (вывод формулы) . Потенциальная энергия упруго деформированного тела (вывод фор-мулы) .
15. Механическая работа. Мощность. Работа как мера изменения механической энергии тела. Теоремы об изменении кинетической и потенциальной энергий (вывод формул) . Закон сохранения механической энергии (вывод формулы) . Границы применимости закона сохранения механической энергии.
16. Удар. Упругий удар. Неупругий удар. Выполнение законов сохранения импульса и энергии при ударе.
Принцип независимости действия сил формулируется так: при одновременном действии на материальную точку нескольких сил ее ускорение равно векторной сумме ускорений, которые эта точка получила бы от действия каждой силы в отдельности .
Пусть к материальной точке А приложены силы F1 и F2 равнодействующая которых равна F на основании аксиомы параллелограмма запишем:
Разделив обе части равенства на массу точки m , получим:
Применяя последовательно аксиому параллелограмма, можно показать, что при одновременном действии на материальную точку нескольких сил ее ускорение будет таким, как если бы действовала одна равнодействующая сила F = ΣFi .
Пользуясь изложенным выше принципом независимости действия сил, выведем уравнение движения материальной точки в дифференциальной форме.
Дифференциальные уравнения движения материальной точки
Пусть материальная точка А массой m движется в плоскости чертежа под действием равнодействующей силы F = ΣFi с ускорением а , тогда:

Спроецируем это векторной равенство на две взаимно-перпендикулярные оси координат x и y (оси и вектор силы F лежат в одной плоскости) и получим уравнение плоского движения материальной точки в координатной форме:
Применяя теорему о проекции ускорения на координатную ось, эти уравнения можно записать в виде дифференциальных уравнений плоского движения точки:
ΣX = m(d 2 x/dt 2 ) ; ΣY = m(d 2 y/dt 2 ) ,
где ΣX и ΣY – алгебраические суммы проекций сил, действующих на точку, на соответствующие координатные оси; x и y – текущие координаты точки.
С помощью полученных дифференциальных зависимостей решаются две основные задачи динамики :
- по заданному движению точки определяют действующие на нее силы;
- зная действующие на точку силы, определяют ее движение.
В тех случаях, когда при решении задач имеем дело с несвободной материальной точкой, необходимо применять принцип освобождаемости, т. е. отбросить связи и заменить их реакциями, учитывая последние в уравнении движения наравне с действующими на точку активными силами.
Пример решения первой задачи динамики
Задача: движение тела массой m = 0,5 кг выражается уравнениями:
x = 2t ; y = 3 + t – 5t 2 ,
где x и y (в сантиметрах) – координаты точки в момент времени t (в секундах) .
Определить силу, действующую на тело.
Решение.
Данный пример относится к первой задаче динамики. Прежде всего, пользуясь теоремой о проекции ускорения на координатную ось, определим проекции ускорения на оси x и y :
ax = d 2 x/dt 2 = 0 ; ay = d 2 y/dt 2 = - 10 см/с 2 = - 0,1 м/с 2 .
Подставив эти значения в уравнение движения материальной точки, получим:
X = max = 0,5×0 = 0 Н ; Y = may = 0,5×(- 0,1) = - 0,05 Н .
По полученным значениям проекций силы на координатные оси можно сделать вывод, что она параллельна оси ординат, направлена в сторону отрицательных ординат и по модулю равна:
F = √(X 2 + Y 2 ) = |Y| = 0,05 Н.
Пример решения второй задачи динамики
Задача: на материальную точку массой m = 4 кг , лежащую на гладкой горизонтальной плоскости, действует горизонтальная сила F = 12 Н .
С какой скоростью будет двигаться материальная точка через время t = 10 с , если до приложения силы точка находилась в состоянии покоя?
Решение.
Данный пример относится ко второй задаче динамики.
Так как данная материальная точка лежит на гладкой горизонтальной плоскости, то под действием горизонтальной постоянной силы F точка будет двигаться прямолинейно равноускоренно. Направив координатную ось x вдоль траектории движения точки (вдоль вектора силы F) , запишем уравнение ее движения:
Спроецировав на ось x действующие на точку силы, и подставив в это уравнение значение массы m , определим ускорение точки:
a = ΣX/m = F/m = 12/4 = 3 м/с 2 .
Применим формулу скорости равноускоренного движения и подставим в нее значения, получим:
1. Радиус-вектор, его проекции. Вектор перемещения, траектория, путь, закон движения. Принцип независимости движения. Средняя и мгновенная скорости. Сложение скоростей. Прямолинейное равномерное движение.
Ра́диус-ве́ктор (обычно обозначается или просто ) — вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
Длина радиус-вектора, или его модуль, определяет расстояние, на котором точка находится от начала координат, а стрелка указывает направление на эту точку пространства.
На плоскости углом радиус-вектора называется угол, на который радиус-вектор повёрнут относительно оси абсцисс в направлении против часовой стрелки.
Проекциями радиус-векторана Ох и Оу являются координаты конца этого вектора, rx, ry и rz. Проекция может быть положительной и отрицательной. Координаты вектора определяют его модуль. Модуль = корень из суммы квадратов проекций.

Перемеще́ние (в кинематике) —изменение местоположения физического тела в пространстве относительно выбранной системы отсчёта. Также перемещением называют вектор, характеризующий это изменение. Можно определить перемещение, как изменение радиус-вектора точки: . Вектор перемещения имеет компоненты.
Траектория материа́льной то́чки — линия в пространстве, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве относительно выбранной системы отсчёта.
Путь — длина участка траектории материальной точки.
Закон движения — математическая формулировка того, как движется тело или как происходит движение более общего вида или набор зависимостей, которые выявляют все данные о движении точки.
В классической механике материальной точки закон движения представляет собой три зависимости трёх пространственных координат от времени, либо зависимость одной векторной величины (радиус-вектора) от времени, вида

Можно записать в векторном виде для радиус-вектора.
Принцип независимости движений: если тело участвует одновременно в нескольких движениях, то каждое из этих движений происходит независимо от других.
Средняя скорость - векторная физическая величина, сонаправленная с перемещением и равная отношению изменения координаты точки к интервалы времени, за которое это перемещение было совершено.
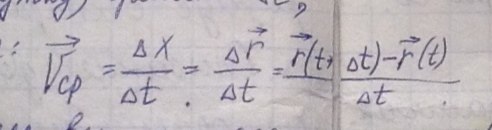
Средняя путевая скорость (средний модуль скорости) — скалярная физическая величина, характеризующая отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден.

Мгновенная скорость точки определяется как предел отношения перемещения к малому промежутку времени, за которое оно совершено, предел, к которому стремится вектор средней скорости при .

.
Это производная радиус-вектора по времени. Направлена по касательной к траектории в сторону движения.
При рассмотрении сложного движения (то есть когда точка или тело движется в одной системе отсчёта, которая движется относительно другой) возникает вопрос о связи скоростей в 2 системах отсчёта.
В классической механике абсолютная скорость точки равна векторной сумме
её относительной и переносной скоростей:

Данное равенство представляет собой содержание утверждения теоремы о сложении скоростей.
Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости (относительно неподвижной системы) той точки подвижной системы отсчёта, в которой в данный момент времени находится тело.
Равномерное прямолинейное движение — механическое движение, при котором мгновенная скорость тела в любой момент времени постоянна по величине и направлению.
Расстояние, пройденное точкой за время , задаётся в этом случае формулой .
Равномерное прямолинейное движение — это движение, при котором тело (точка) за любые равные и бесконечно малые промежутки времени совершает одинаковые перемещения. Вектор скорости точки остаётся неизменным, а её перемещение есть произведение вектора скорости и времени.

.


,
где — начальная координата точки, — проекция вектора скорости на координатную ось.
1. Радиус-вектор, его проекции. Вектор перемещения, траектория, путь, закон движения. Принцип независимости движения. Средняя и мгновенная скорости. Сложение скоростей. Прямолинейное равномерное движение.
Ра́диус-ве́ктор (обычно обозначается или просто ) — вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
Длина радиус-вектора, или его модуль, определяет расстояние, на котором точка находится от начала координат, а стрелка указывает направление на эту точку пространства.
На плоскости углом радиус-вектора называется угол, на который радиус-вектор повёрнут относительно оси абсцисс в направлении против часовой стрелки.
Проекциями радиус-векторана Ох и Оу являются координаты конца этого вектора, rx, ry и rz. Проекция может быть положительной и отрицательной. Координаты вектора определяют его модуль. Модуль = корень из суммы квадратов проекций.

Перемеще́ние (в кинематике) —изменение местоположения физического тела в пространстве относительно выбранной системы отсчёта. Также перемещением называют вектор, характеризующий это изменение. Можно определить перемещение, как изменение радиус-вектора точки: . Вектор перемещения имеет компоненты.
Траектория материа́льной то́чки — линия в пространстве, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве относительно выбранной системы отсчёта.
Путь — длина участка траектории материальной точки.
Закон движения — математическая формулировка того, как движется тело или как происходит движение более общего вида или набор зависимостей, которые выявляют все данные о движении точки.
В классической механике материальной точки закон движения представляет собой три зависимости трёх пространственных координат от времени, либо зависимость одной векторной величины (радиус-вектора) от времени, вида

Можно записать в векторном виде для радиус-вектора.
Принцип независимости движений: если тело участвует одновременно в нескольких движениях, то каждое из этих движений происходит независимо от других.
Средняя скорость - векторная физическая величина, сонаправленная с перемещением и равная отношению изменения координаты точки к интервалы времени, за которое это перемещение было совершено.
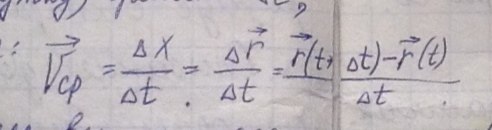
Средняя путевая скорость (средний модуль скорости) — скалярная физическая величина, характеризующая отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден.

Мгновенная скорость точки определяется как предел отношения перемещения к малому промежутку времени, за которое оно совершено, предел, к которому стремится вектор средней скорости при .

.
Это производная радиус-вектора по времени. Направлена по касательной к траектории в сторону движения.
При рассмотрении сложного движения (то есть когда точка или тело движется в одной системе отсчёта, которая движется относительно другой) возникает вопрос о связи скоростей в 2 системах отсчёта.
В классической механике абсолютная скорость точки равна векторной сумме
её относительной и переносной скоростей:

Данное равенство представляет собой содержание утверждения теоремы о сложении скоростей.
Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости (относительно неподвижной системы) той точки подвижной системы отсчёта, в которой в данный момент времени находится тело.
Равномерное прямолинейное движение — механическое движение, при котором мгновенная скорость тела в любой момент времени постоянна по величине и направлению.
Расстояние, пройденное точкой за время , задаётся в этом случае формулой .
Равномерное прямолинейное движение — это движение, при котором тело (точка) за любые равные и бесконечно малые промежутки времени совершает одинаковые перемещения. Вектор скорости точки остаётся неизменным, а её перемещение есть произведение вектора скорости и времени.

.

,
где — начальная координата точки, — проекция вектора скорости на координатную ось.
Мы уже говорили об основах классической механики. Настала пора поговорить о них подробнее и затронуть в обсуждении чуть больше, чем просто основу. В этой статье мы подробно разберем основные законы классической механики. Как вы уже догадались, речь пойдет о законах Ньютона.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Был долго этот мир глубокой тьмой окутан
Да будет свет, и тут явился Ньютон.
Но сатана недолго ждал реванша -
Пришел Эйнштейн, и стало все как раньше.
(Эпиграмма 20-го века)
Что стало, когда пришел Эйнштейн, читайте в отдельном материале про релятивистскую динамику. А мы пока приведем формулировки и примеры решения задач на каждый закон Ньютона.
Первый закон Ньютона
Первый закон Ньютона гласит:
Существуют такие системы отсчета, называемые инерциальными, в которых тела движутся равномерно и прямолинейно, если на них не действуют никакие силы или действие других сил скомпенсировано.
Проще говоря, суть первого закона Ньютона можно сформулировать так: если мы на абсолютно ровной дороге толкнем тележку и представим, что можно пренебречь силами трения колес и сопротивления воздуха, то она будет катиться с одинаковой скоростью бесконечно долго.
Инерция – это способность тела сохранять скорость как по направлению, так и по величине, при отсутствии воздействий на тело. Первый закон Ньютона еще называют законом инерции.
Понятно, что таких систем, где тележку толкнули, а она покатилась без действия внешних сил, на самом деле не бывает. На тела всегда действуют силы, причем скомпенсировать действие этих сил полностью практически невозможно.
Например, все на Земле находится в постоянном поле силы тяжести. Когда мы передвигаемся (не важно, ходим пешком, ездим на машине или велосипеде), нам нужно преодолевать множество сил: силу трения качения и силу трения скольжения, силу тяжести, силу Кориолиса.

Второй закон Ньютона
Помните пример про тележку? В этот момент мы приложили к ней силу! Интуитивно понятно, что тележка покатится и вскоре остановится. Это значит, ее скорость изменится.
В реальном мире скорость тела чаще всего изменяется, а не остается постоянной. Другими словами, тело движется с ускорением. Если скорость нарастает или убывает равномерно, то говорят, что движение равноускоренное.
Если рояль падает с крыши дома вниз, то он движется равноускоренно под действием постоянного ускорения свободного падения g. Причем любой дугой предмет, выброшенный из окна на нашей планете, будет двигаться с тем же ускорением свободного падения.
Второй закон Ньютона устанавливает связь между массой, ускорением и силой, действующей на тело. Приведем формулировку второго закона Ньютона:
Ускорение тела (материальной точки) в инерциальной системе отсчета прямо пропорционально приложенной к нему силе и обратно пропорционально массе.
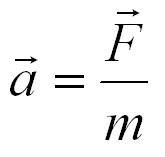

Если на тело действует сразу несколько сил, то в данную формулу подставляется равнодействующая всех сил, то есть их векторная сумма.
В такой формулировке второй закон Ньютона применим только для движения со скоростью, много меньшей, чем скорость света .
Существует более универсальная формулировка данного закона, так называемый дифференциальный вид.
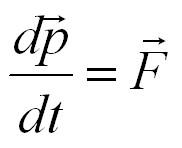
В любой бесконечно малый промежуток времени dt сила, действующая на тело, равна производной импульса тела по времени.
Третий закон Ньютона
В чем состоит третий закон Ньютона? Этот закон описывает взаимодействие тел.
3 закон Ньютона говорит нам о том, что на любое действие найдется противодействие. Причем, в прямом смысле:
Два тела воздействуют друг на друга с силами, противоположными по направлению, но равными по модулю.
Формула, выражающая третий закон Ньютона:
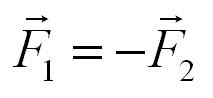
Другими словами, третий закон Ньютона - это закон действия и противодействия.

Пример задачи на законы Ньютона
Вот типичная задачка на применение законов Ньютона. В ее решении используются первый и второй законы Ньютона.
Десантник раскрыл парашют и опускается вниз с постоянной скоростью. Какова сила сопротивления воздуха? Масса десантника – 100 килограмм.
Решение:
Движение парашютиста – равномерное и прямолинейное, поэтому, по первому закону Ньютона, действие сил на него скомпенсировано.
На десантника действуют сила тяжести и сила сопротивления воздуха. Силы направлены в противоположные стороны.
По второму закону Ньютона, сила тяжести равна ускорению свободного падения, умноженному на массу десантника.
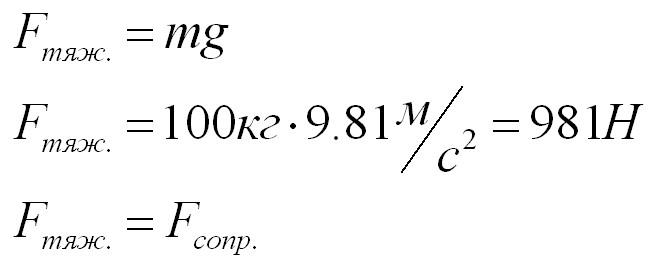
Ответ: Сила сопротивления воздуха равна силе тяжести по модулю и противоположна направлена.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
А вот еще одна физическая задачка на понимание действия третьего закона Ньютона.
Комар ударяется о лобовое стекло автомобиля. Сравните силы, действующие на автомобиль и комара.
Решение:
По третьему закону Ньютона, силы, с которыми тела действуют друг на друга, равны по модулю и противоположны по направлению. Сила, с которой комар действует на автомобиль, равна силе, с которой автомобиль действует на комара.
Другое дело, что действие этих сил на тела сильно отличаются вследствие различия масс и ускорений.
Исаак Ньютон: мифы и факты из жизни
На момент публикации своего основного труда Ньютону было 45 лет. За свою долгую жизнь ученый внес огромный вклад в науку, заложив фундамент современной физики и определив ее развитие на годы вперед.
Он занимался не только механикой, но и оптикой, химией и другими науками, неплохо рисовал и писал стихи. Неудивительно, что личность Ньютона окружена множеством легенд.
Ниже приведены некоторые факты и мифы из жизни И. Ньютона. Сразу уточним, что миф – это не достоверная информация. Однако мы допускаем, что мифы и легенды не появляются сами по себе и что-то из перечисленного вполне может оказаться правдой.
- Факт. Исаак Ньютон был очень скромным и застенчивым человеком. Он увековечил себя благодаря своим открытиям, однако сам никогда не стремился к славе и даже пытался ее избежать.
- Миф. Существует легенда, согласно которой Ньютона осенило, когда на наго в саду упало яблоко. Это было время чумной эпидемии (1665-1667), и ученый был вынужден покинуть Кембридж, где постоянно трудился. Точно неизвестно, действительно ли падение яблока было таким роковым для науки событием, так как первые упоминания об этом появляются только в биографиях ученого уже после его смерти, а данные разных биографов расходятся.
- Факт. Ньютон учился, а потом много работал в Кембридже. По долгу службы ему нужно было несколько часов в неделю вести занятия у студентов. Несмотря на признанные заслуги ученого, занятия Ньютона посещались плохо. Бывало, что на его лекции вообще никто не приходил. Скорее всего, это связано с тем, что ученый был полностью поглощен своими собственными исследованиями.
- Миф. В 1689 году Ньютон был избран членом Кембриджского парламента. Согласно легенде, более чем за год заседания в парламенте вечно поглощенный своими мыслями ученый взял слово для выступления всего один раз. Он попросил закрыть окно, так как был сквозняк.
- Факт. Неизвестно, как бы сложилась судьба ученого и всей современной науки, если бы он послушался матери и начал заниматься хозяйством на семейной ферме. Только благодаря уговорам учителей и своего дяди юный Исаак отправился учиться дальше вместо того, чтобы сажать свеклу, разбрасывать по полям навоз и по вечерам выпивать в местных пабах.
Дорогие друзья, помните - любую задачу можно решить! Если у вас возникли проблемы с решением задачи по физике, посмотрите на основные физические формулы. Возможно, ответ перед глазами, и его нужно просто рассмотреть. Ну а если времени на самостоятельные занятия совершенно нет, специализированный студенческий сервис всегда к вашим услугам!
В самом конце предлагаем посмотреть видеоурок на тему "Законы Ньютона".
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Принцип независимости действия сил формулируется так: при одновременном действии на материальную точку нескольких сил ее ускорение равно векторной сумме ускорений, которые эта точка получила бы от действия каждой силы в отдельности.
Пусть к материальной точке А приложены силы F1и F2, равнодействующая которых равна F. На основании аксиомы параллелограмма запишем
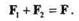
Разделим обе части равенства на массу точки, получим


Применяя последовательно аксиому параллелограмма, можно сказать, что при одновременном действии на материальную точку нескольких сил ее ускорение будет таким, как если бы действовала одна равнодействующая сила
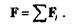
Пользуясь принципом независимости действия сил, выведем уравнение движения материальной точки в дифференциальной форме.
Пусть материальная точка А массой т движется в плоскости чертежа под действием силы F = Fi с ускорением а, тогда

Спроецируем это векторное равенство на две взаимно перпендикулярные оси координат х и у (оси и вектор силы F лежат в одной плоскости) и получим уравнения плоского движения материальной точки в координатной форме:

Применяя теорему о проекции ускорения на координатную ось, можно эти уравнения записать в виде дифференциальных уравнений плоского движения материальной точки:

В этих уравнениях X, Y — алгебраические суммы проекций сил,
действующих на точку, на соответствующие координатные оси; х и у — текущие координаты точки.
С помощью выведенных в этом параграфе уравнений решаются две основные задачи динамики: 1) по заданному движению точки определить действующие на нее силы; 2) зная действующие на точку силы, определить ее движение.
В тех случаях, когда при решении задач имеем дело с несвободной материальной точкой, необходимо применять принцип освобождаемости, т. е. отбросить связи и заменить их реакциями, учитывая последние в уравнениях движения наравне с действующими на точку активными силами.
Пример 13.1.Движение тела массой 0,5 кг выражается уравнениями

где х и у — в сантиметрах, t—в секундах. Определить силу, действующую на тело.
Решение. Данный пример относится к первой задаче динамики. Прежде всего, пользуясь теоремой о проекции ускорения на координатную ось, определим проекции ускорения на оси х и у:

Подставив эти значения в уравнения движения материальной точки, получим:

По проекциям силы, действующей на тело, видно, что она параллельна оси ординат, направлена в сторону отрицательных ординат и по модулю равна


Пример 13.2. Кривошип ОА длиной l, вращаясь равномерно с угловой скоростью , перемещает кулису, движущуюся поступательно вдоль направляющих I—I (рис. 13.1). Найти, пренебрегая трением, чему при этом равна сила давления F камня А на кулису, если сила тяжести ее равна G.
Решение. Данный пример относится к первой задаче динамики.
Применим принцип освобождаемости, отбросим связи кулисы и заменим их реакциями. Реакция N перпендикулярна направляющим кулисы, а сила давления F перпендикулярна кулисе, так как по условию трением пренебрегаем.
Кулиса движется возвратно-поступательно, следовательно, все ее точки движутся одинаково. Составим уравнение движения проекции точки А на ось х, которое и будет кинематическим уравнением движения кулисы:

Применив теорему о проекции ускорения на координатную ось, определим ускорение кулисы

Составим уравнение движения кулисы в координатной форме:

Спроецировав действующие накулису силы на осьд: и подставивзначения массы и ускорения, получим


Следовательно, сила давления ползуна на кулису изменяется пропорционально расстоянию кулисы от оси кривошипа.
Пример 13.3.На материальную точку массой 4 кг лежащую на гладкой горизонтальной плоскости действует горизонтальная сила F = 12 Н. С какой скоростью будет двигаться материальная точка через t = 10 с, если до приложения силы эта точка находилась в покое?
Решение. Данный пример относится ко второй задаче динамики.
Так как данная материальная точка лежит на гладкой горизонтальной плоскости, то под действием горизонтальной постоянной силы F точка будет двигаться прямолинейно равноускоренно. Направив ось дс вдоль траектории точки, запишем уравнение движения:

Спроецировав на ось х действующие на точку силы и подставив в это уравнение значение массы, определим ускорение

Применим формулу скорости равноускоренного движения

Подставив значения, получим
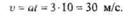
Пример 13.4. В результате полученного толчка кирпич начал скользить с начальной скоростью 0 =2 м/с по неподвижной ленте конвейера, расположенного под углом = /6 рад к горизонту. Определить перемещение s кирпича за про-

межуток времени t = 2с, если коэффициент трения скольжения кирпича о ленту конвейера f = 0,4; кирпич считать точечной массой (рис 13.2).
Решение. Данный пример относится ко второй задаче динамики. Выберем систему координат хОу таким образом, чтобы начало координат было в начальном положении тела, ось х была направлена вдоль ленты конвейера вниз, а ось у — перпендикулярно ленте конвейера вверх. Применив принцип освобождаемое, рассмотрим кирпич как материальную точку, движущуюся вдоль оси х под действием силы тяжести G, нормальной реакции N и силы трения Fтр.
Составим уравнения движения материальной точки:
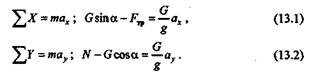
Кроме того, на основании второго закона трения скольжения можно записать

Так как материальная точка движется вдоль оси х, то ау = 0, в результате чего из уравнения (13.2) имеем

Подставив это выражение в уравнение (13.3), получим

Полученное выражение подставим в уравнение (13.1):

Сокращая это равенство на G и учитывая, что ах =а ,определим ускорение кирпича:

или, вынеся gcosa за скобку, получим

Так как правая часть этого равенства содержит только постоянные величины, то ускорение кирпича—величина постоянная, причем возможны три случая движения:
1) если tg > f, то а > 0 и движение будет равноускоренным;
2) если tg = f, тo a = 0 и движение будет равномерным;
3) если tg f, т. е. а > 0, следовательно, движение кирпича было равноускоренным.
Движение материальной точки,
© 2014-2022 — Студопедия.Нет — Информационный студенческий ресурс. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав (0.008)
Читайте также:

