Основные понятия теории игр кратко

Обновлено: 30.06.2024

Содержание статьи:

Что такое теория игр простыми словами

Теория игр — это теоретическая основа для понимания социальных ситуаций между конкурирующими игроками. В некотором смысле теория игр — это наука о стратегии или, по крайней мере, об оптимальном процессе принятия решений независимыми и конкурирующими субъектами в стратегической обстановке.

Ключевыми пионерами теории игр были математик Джон фон Нейман и экономист Оскар Моргенштерн в 1940-х годах. Многие считают математика Джона Нэша первым значительным продолжением работ фон Неймана и Моргенштерна.

Предполагается, что игроки в игре рациональны и будут стремиться максимизировать свои выигрыши в игре.

Основы и суть теории игр

В центре внимания теории игр находится игра, которая служит моделью интерактивной ситуации среди рациональных игроков. Ключ к теории игр состоит в том, что выигрыш одного игрока зависит от стратегии, реализованной другим игроком. Игра определяет личности, предпочтения и доступные стратегии игроков, а также то, как эти стратегии влияют на результат. В зависимости от модели могут потребоваться различные другие требования или предположения.

Теория игр имеет широкий спектр приложений, включая психологию, эволюционную биологию, войну, политику, экономику и бизнес. Несмотря на многочисленные достижения, теория игр по-прежнему остается молодой и развивающейся наукой.

Согласно теории игр, действия и выбор всех участников влияют на результат каждого.

Терминология теории игр

Каждый раз, когда у нас возникает ситуация с двумя или более игроками, которая связана с известными выплатами или поддающимися количественной оценке последствиями, мы можем использовать теорию игр, чтобы определить наиболее вероятные результаты. Начнем с определения нескольких терминов, обычно используемых при изучении теории игр:

Равновесие Нэша

Однако это обычно происходит в играх с более сложными элементами, чем два выбора двух игроков. В одновременных играх, которые повторяются во времени, одно из этих множественных равновесий достигается после некоторых проб и ошибок. Этот сценарий различных вариантов выбора сверхурочно до достижения равновесия наиболее часто разыгрывается в деловом мире, когда две фирмы определяют цены на взаимозаменяемые продукты, такие как авиабилеты или безалкогольные напитки.

Влияние на экономику и бизнес

В бизнесе теория игр полезна для моделирования конкурирующего поведения экономических агентов. У предприятий часто есть несколько стратегических вариантов, которые влияют на их способность реализовать экономическую выгоду. Например, предприятия могут столкнуться с дилеммами, например: отказаться от существующих продуктов или разработать новые, снизить цены по сравнению с конкурентами или использовать новые маркетинговые стратегии. Экономисты часто используют теорию игр, чтобы понять поведение олигополистических фирм. Это помогает предсказать вероятные результаты, когда фирмы будут проявлять определенное поведение, например, сговор.

Двадцать теоретиков игр были удостоены Нобелевской премии по экономическим наукам за их вклад в эту дисциплину.

Типы теории игр

Хотя существует много типов теорий игр (например, симметричные / асимметричные, одновременные / последовательные и др.), наиболее распространенными являются теории кооперативных и некооперативных игр. Теория кооперативных игр изучает, как взаимодействуют коалиции или кооперативные группы, когда известны только выигрыши. Это игра между коалициями игроков, а не между отдельными людьми, и в ней задается вопрос, как формируются группы и как они распределяют выигрыш между игроками.

Примеры теории игр

Дилемма заключенного

Дилемма Заключенного является наиболее известным примером теории игр. Рассмотрим пример двух преступников, арестованных за преступление. У прокуратуры нет веских доказательств, чтобы их осудить. Однако, чтобы получить признание, чиновники выводят заключенных из одиночных камер и допросят каждого в отдельных камерах. Ни у одного из заключенных нет средств общаться друг с другом. Официальные лица представляют четыре сделки, часто отображаемые в виде квадрата 2 x 2.

Если оба признаются, каждый из них получит пятилетний тюремный срок.
Если заключенный 1 признается, а заключенный 2 — нет, то заключенный 1 получит три года, а заключенный 2 — девять лет.
Если заключенный 2 признается, а заключенный 1 — нет, то заключенный 1 получит 10 лет, а заключенный 2 — два года.
Если ни один из них не признается, каждый отсидит по два года тюрьмы.

Самая выгодная стратегия — не признаться. Однако ни один из них не осведомлен о стратегии другого, и без уверенности в том, что один из них не признается, оба, скорее всего, признаются и будут приговорены к пяти годам тюремного заключения. Равновесие Нэша предполагает, что в дилемме заключенного оба игрока сделают ход, который лучше для них по отдельности, но хуже для всех вместе.

Игра Диктатор и Ультиматум

Это простая игра, в которой игрок A должен решить, как разделить денежный приз с игроком B, который не участвует в принятии решения с игроком A. Хотя сама по себе эта стратегия не является теорией игр, она дает некоторые интересные сведения о поведении людей. Эксперименты показывают, что около 50% держат все деньги при себе, 5% делят их поровну, а остальные 45% дают другому участнику меньшую долю.

Игра в диктатора тесно связана с игрой в ультиматум, в которой Игроку А дается определенная сумма денег, часть которой должна быть отдана Игроку Б, который может принять или отклонить данную сумму. Загвоздка в том, что если второй игрок отклоняет предложенную сумму, ни A, ни B ничего не получают. Игры Диктатор и Ультиматум преподают важные уроки для таких вопросов, как благотворительность и филантропия.

Дилемма волонтера

В дилемме волонтера кто-то должен взять на себя рутинную работу или работу для общего блага. Наихудший возможный исход будет реализован, если никто не станет добровольцем. Например, рассмотрим компанию, в которой широко распространено мошенничество в области бухгалтерского учета, хотя высшее руководство об этом не подозревает. Некоторые младшие сотрудники бухгалтерии знают о мошенничестве, но не решаются сообщить об этом высшему руководству, потому что это приведет к увольнению сотрудников, причастных к мошенничеству, и, скорее всего, к судебному преследованию.

Признание разоблачителем также может иметь определенные последствия в будущем. Но если никто не станет добровольцем, крупномасштабное мошенничество может привести к банкротству компании и потере всех рабочих мест.

Игра Сороконожка

Игра с сороконожкой завершается, как только игрок берет тайник, причем этот игрок получает большую часть, а другой игрок — меньшую часть. В игре заранее определено общее количество раундов, которое заранее известно каждому игроку.

Ограничения теории игр

Самая большая проблема теории игр состоит в том, что, как и большинство других экономических моделей, она основана на предположении, что люди являются рациональными субъектами, корыстолюбивы и стремятся максимизировать полезность. Конечно, мы социальные существа, которые действительно сотрудничают и заботятся о благополучии других, часто за свой счет. Теория игр не может объяснить тот факт, что в некоторых ситуациях мы можем попасть в равновесие по Нэшу, а в других случаях — нет, в зависимости от социального контекста и игроков.

Резюме

Теоретически эти игры можно отнести к категории подобных дилемм заключенного, игре диктатора, ястребу и голубю, Баху или Стравинскому, а также нескольким другим вариациям.

Каковы предположения об этих играх?

Как и многие экономические модели, теория игр также содержит набор строгих предположений, которые должны выполняться для того, чтобы теория делала хорошие прогнозы на практике. Во-первых, все игроки являются рациональными субъектами, максимизирующими полезность, которые имеют полную информацию об игре, правилах и последствиях. Игрокам не разрешается общаться или взаимодействовать друг с другом. Возможные исходы не только известны заранее, но и не могут быть изменены. Теоретически количество игроков в игре может быть бесконечным, но большинство игр будет рассматриваться в контексте только двух игроков.

Что такое равновесие по Нэшу?

Равновесие по Нэшу — это важная концепция, относящаяся к стабильному состоянию в игре, в котором ни один игрок не может получить преимущество путем одностороннего изменения стратегии, при условии, что другие участники также не меняют свои стратегии. Равновесие Нэша обеспечивает концепцию решения в некооперативной (состязательной) игре. Оно названо в честь Джона Нэша, получившего Нобелевскую премию в 1994 году за свою работу.

Кто придумал теорию игр?

Теория игр в значительной степени приписывается работам математика Джона фон Неймана и экономиста Оскара Моргенштерна в 1940-х годах и широко развивалась многими другими исследователями и учеными в 1950-х годах. По сей день теория игр остается областью активных исследований и прикладной науки.

Теория игр — это теоретическая основа для понимания социальных ситуаций между конкурирующими игроками и обеспечения оптимального принятия решений независимыми и конкурирующими субъектами в стратегической обстановке.
Используя теорию игр, можно разложить реальные сценарии для таких ситуаций, как ценовая конкуренция и выпуск продукции (и многое другое), и спрогнозировать их результаты.
Сценарии включают дилемму заключенного и диктаторскую игру среди многих других.

А на этом сегодня все про Теорию Игр. Делитесь статьей в социальных сетях и мессенджерах и добавляйте сайт в закладки. Успехов и до новых встреч на страницах проекта Тюлягин!

Ситуация называется конфликтной, если в ней участвуют стороны, интересы которых полностью или частично противоположны.

Игра — это действительный или формальный конфликт, в котором имеется по крайней мере два участника (игрока), каждый из которых стремится к достижению собственных целей.

Допустимые действия каждого из игроков, направленные на достижение некоторой цели, называются правилами игры.

Количественная оценка результатов игры называется платежом.

Игра называется парной, если в ней участвуют только две стороны (два лица).

Парная игра называется игрой с нулевой суммой, если сумма платежей равна нулю, т. е. если проигрыш одного игрока равен выигрышу второго.

Однозначное описание выбора игрока в каждой из возможных ситуаций, при которой он должен сделать личный ход, называется стратегией игрока.

Стратегия игрока называется оптимальной, если при многократном повторении игры она обеспечивает игроку максимально возможный средний выигрыш.

Пусть имеется два игрока, один из которых может выбрать i-ю стратегию из m своих возможных стратегий (i= ), а второй, не зная выбора первого, выбирает j-ю стратегию из п своих возможных стратегий (j= ). В результате первый игрок выигрывает величину а_ij, а второй проигрывает эту величину.

Из чисел а_ij составим матрицу

Строки матрицы A соответствуют стратегиям первого игрока, а столбцы — стратегиям второго. Эти стратегии называются чистыми.

Матрица А называется платежной (или матрицей игры).

Игру, определяемую матрицей А, имеющей m строк и n столбцов, называют конечной игрой размерности m×n.

Число α = называется нижней ценой игры или максимином, а соответствующая ему стратегия (строка) — максиминной.

Число β = называется верхней ценой игры или минимаксом, а соответствующая ему стратегия игрока (столбец) — минимаксной.

Теорема 1.Нижняя цена игры всегда не превосходит верхней цены игры.

Если α = β = υ, то число υ называется ценой игры.

Игра, для которой α = β, называется игрой с седловой точкой.

Для игры с седловой точкой нахождение решения состоит в выборе максиминной и минимаксной стратегий, которые являются оптимальными.

Если игра, заданная матрицей, не имеет седловой точки, то для нахождения ее решения используются смешанные стратегии.

Вектор, каждая из компонент которого показывает относительную частоту использования игроком соответствующей чистой стратегии, называется смешанной стратегией данного игрока.

Из данного определения непосредственно следует, что сумма компонент указанного вектора равна единице, а сами компоненты не отрицательны. Обычно смешанную стратегию первого игрока обозначают как вектор U = (u₁, u₂ . u_m), а второго игрока — как вектор Z = (z₁, z₂ . z_n), где u_i ≥ 0 (i= ), z_i ≥ 0 (j= ),

Если U* — оптимальная стратегия первого игрока, a Z* — оптимальная стратегия второго игрока, то число

является ценой игры.

Определение оптимальных стратегий и цены игры и составляет процесс нахождения решения игры.

Теорема 2 Всякая матричная игра с нулевой суммой имеет решение в смешанных стратегиях.

Теорема 3 Для того чтобы число v было ценой игры, a U* и Z* — оптимальными стратегиями, необходимо и достаточно выполнение неравенств

Если теорема 2 дает ответ на вопрос о существовании решения игры, то следующая теорема дает ответ на вопрос, как найти это решение для игр 2×2, 2×n и n×2, примеры которых приведены ниже.

Теорема 4 Если один из игроков применяет оптимальную смешанную стратегию, то его выигрыш равен цене игры υ вне зависимости от того, с какими частотами будет применять второй игрок стратегии, вошедшие в оптимальную (в том числе и чистые стратегии).

Пример1. Найти решение игры, заданной матрицей и дать геометрическую интерпретацию этого решения.

Решение. Прежде всего проверим наличие седловой точки в данной матрице. Для этого найдем минимальные элементы в каждой из строк (2 и 4) и максимальные элементы в каждом из столбцов (6 и 5). Значит, нижняя цена игры α = mах (2; 4) =4, а верхняя цена игры β = min (6; 5) = 5. Так как α = 4 ≠ β = 5, то решением игры являются смешанные оптимальные стратегии, а цена игры v заключена в пределах 4≤ υ ≤!5.

Предположим, что для игрока А стратегия задается вектором U = (u₁; u₂). Тогда на основании теоремы 4 при применении игроком В чистой стратегии В₁ или В₂ игрок А получит средний выигрыш, равный цене игры, т. е.

Помимо двух записанных уравнений относительно и добавим уравнение, связывающее частоты и .

Решая полученную систему трех уравнений с тремя неизвестными, находим =2/5; =3/5; υ = 22/5.

Найдем теперь оптимальную стратегию для игрока В. Пусть стратегия для данного игрока задается вектором Z=(z₁; z₂).

Решая систему уравнений, состоящую из каких-нибудь двух уравнений, взятых из последней системы, получим =1/5; =4/5. Следовательно, решением игры являются смешанные стратегии U* = (2/5; 3/5) и Z* = (1/5; 4/5), а цена игры υ = 22/5.

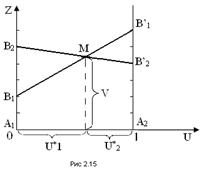
Дадим теперь геометрическую интерпретацию решения данной игры. Для этого на плоскости uOz введем систему координат и на оси Оu отложим отрезок единичной длины А₁А₂, каждой точке которого поставим в соответствие некоторую смешанную стратегию U= (u₁, u₂) = (u₁, 1- u₁)

(рис. 1). В частности, точке А₁ (0; 1) отвечает стратегия A₁, точке А₂ (1; 0) —стратегия А₂ и т. д.

Пример 2. Швейное предприятие планирует к массовому выпуску новую модель одежды. Спрос на эту модель не может быть точно определен. Однако можно предположить, что его величина характеризуется тремя возможными состояниями (I, II, III). С учетом этих состояний анализируются три возможных варианта выпуска данной модели (А, Б, В). Каждый из этих вариантов требует своих затрат и обеспечивает в конечном счете различный эффект. Прибыль (тыс. руб.), которую получает предприятие при данном объеме выпуска модели и соответствующем состоянии спроса, определяется матрицей

Требуется найти объем выпуска модели одежды, обеспечивающий среднюю величину прибыли при любом состоянии спроса.

Решение. Прежде всего проверим, имеет ли исходная матрица седловую точку. Для этого находим минимальные элементы в ее строках (22; 21; 20) и максимальные— в столбцах (22; 23; 24). Максимальным среди минимальных элементов строк является число а = 22, а минимальным среди максимальных элементов столбцов — число р = 22. Таким образом, а = |3 = 22. Число 22 является ценой игры. Игра имеет седловую точку, соответствующую 1 варианту выпуска модели одежды. Объем выпуска модели, соответствующей данному варианту, обеспечивает прибыль в 22 тыс. руб. при любом состоянии спроса.

Используя геометрическую интерпретацию, найдите решение игр, определяемых следующими матрицами.