Метод обратного распространения ошибки нейронной сети кратко
Обновлено: 02.07.2024
Нейронные сети обучаются с помощью тех или иных модификаций градиентного спуска, а чтобы применять его, нужно уметь эффективно вычислять градиенты функции потерь по всем обучающим параметрам. Казалось бы, для какого-нибудь запутанного вычислительного графа это может быть очень сложной задачей, но на помощь спешит метод обратного распространения ошибки.
Открытие метода обратного распространения ошибки стало одним из наиболее значимых событий в области искусственного интеллекта. В актуальном виде он был предложен в 1986 году Дэвидом Э. Румельхартом, Джеффри Э. Хинтоном и Рональдом Дж. Вильямсом и независимо и одновременно красноярскими математиками С. И. Барцевым и В. А. Охониным. С тех пор для нахождения градиентов параметров нейронной сети используется метод вычисления производной сложной функции, и оценка градиентов параметров сети стала хоть сложной инженерной задачей, но уже не искусством. Несмотря на простоту используемого математического аппарата, появление этого метода привело к значительному скачку в развитии искусственных нейронных сетей.
Суть метода можно записать одной формулой, тривиально следующей из формулы производной сложной функции: если $f(x) = g_m(g_(\ldots (g_1(x)) \ldots))$, то $\frac<\partial f> <\partial x>= \frac<\partial g_m><\partial g_>\frac<\partial g_><\partial g_
Backpropagation в одномерном случае
В одномерном случае всё выглядит особенно просто. Пусть $w_0$ — переменная, по которой мы хотим продифференцировать, причём сложная функция имеет вид
\[f(w_0) = g_m(g_(\ldots g_1(w_0)\ldots)),\]
где все $g_i$ скалярные. Тогда
\[f'(w_0) = g_m'(g_(\ldots g_1(w_0)\ldots))\cdot g'_(g_(\ldots g_1(w_0)\ldots))\cdot\ldots \cdot g'_1(w_0)\]
Суть этой формулы такова. Если мы уже совершили forward pass, то есть уже знаем
\[g_1(w_0), g_2(g_1(w_0)),\ldots,g_(\ldots g_1(w_0)\ldots),\]
то мы действуем следующим образом:
берём производную $g_m$ в точке $g_(\ldots g_1(w_0)\ldots)$;
умножаем на производную $g_$ в точке $g_(\ldots g_1(w_0)\ldots)$;
и так далее, пока не дойдём до производной $g_1$ в точке $w_0$.
Проиллюстрируем это на картинке, расписав по шагам дифференцирование по весам $w_i$ функции потерь логистической регрессии на одном объекте (то есть для батча размера 1):

Собирая все множители вместе, получаем:
Таким образом, мы видим, что сперва совершается forward pass для вычисления всех промежуточных значений (и да, все промежуточные представления нужно будет хранить в памяти), а потом запускается backward pass, на котором в один проход вычисляются все градиенты.
В главе, посвящённой матричным дифференцированиям, мы поднимаем вопрос о том, что вычислять частные производные по отдельности — это зло, лучше пользоваться матричными вычислениями. Но есть и ещё одна причина: даже и с матричной производной в принципе не всегда хочется иметь дело. Рассмотрим простой пример. Допустим, что $X^r$ и $X^$ — два последовательных промежуточных представления $N\times M$ и $N\times K$, связанных функцией $X^ = f^(X^r)$. Предположим, что мы как-то посчитали производную $\frac<\partial\mathcal><\partial X^_>$ функции потерь $\mathcal$, тогда
Вы спросите себя: надо ли мне сейчас пойти и прочитать главу учебника про матричное дифференцирование?
Встречный вопрос. Найдите производную функции по вектору $x$:
А как всё поменяется, если $A$ тоже зависит от $x$? Чему равен градиент функции, если $A$ является скаляром? Если вы готовы прямо сейчас взять ручку и бумагу и посчитать всё, то вам, вероятно, не надо читать про матричные дифференцирования. Но мы советуем всё-таки заглянуть в эту главу, если обозначения, которые мы будем дальше использовать, покажутся вам непонятными: единой нотации для матричных дифференцирований человечество пока, увы, не изобрело, и переводить с одной на другую не всегда легко.
Мы же сразу перейдём к интересующей нас вещи: к вычислению градиентов сложных функций.
Градиент сложной функции
Напомним, что формула производной сложной функции выглядит следующим образом:
Теперь разберёмся с градиентами. Пусть $f(x) = g(h(x))$ – скалярная функция. Тогда
\[\left[D_ f \right] (x-x_0) = \langle\nabla_ f, x-x_0\rangle.\]
С другой стороны,
\[\left[D_ g \right] \left(\left[D_h \right] (x-x_0)\right) = \langle\nabla_
То есть $\color f> = \color <\left[D_h \right]>^* \color>g$ — применение сопряжённого к $D_ h$ линейного отображения к вектору $\nabla_ g$.
Эта формула — сердце механизма обратного распространения ошибки. Она говорит следующее: если мы каким-то образом получили градиент функции потерь по переменным из некоторого промежуточного представления $X^k$ нейронной сети и при этом знаем, как преобразуется градиент при проходе через слой $f^k$ между $X^$ и $X^k$ (то есть как выглядит сопряжённое к дифференциалу слоя между ними отображение), то мы сразу же находим градиент и по переменным из $X^$:

Таким образом слой за слоем мы посчитаем градиенты по всем $X^i$ вплоть до самых первых слоёв.
Далее мы разберёмся, как именно преобразуются градиенты при переходе через некоторые распространённые слои.
Градиенты для типичных слоёв
Рассмотрим несколько важных примеров.
$f(x) = u(v(x))$, где $x$ — вектор, а $v(x)$ – поэлементное применение $v$:
Тогда, как мы знаем,
\[\left[D_ f\right] (h) = \langle\nabla_ f, h\rangle = \left[\nabla_ f\right]^T h.\]
\[\begin \left[D_ u\right] \left( \left[ D_ v\right] (h)\right) = \left[\nabla_ u\right]^T \left(v'(x_0) \odot h\right) =\\[0.1cm] = \sum\limits_i \left[\nabla_ u\right]_i v'(x_)h_i = \langle\left[\nabla_ u\right] \odot v'(x_0), h\rangle. \end,\]
где $\odot$ означает поэлементное перемножение. Окончательно получаем
\[\color f = \left[\nabla_u\right] \odot v'(x_0) = v'(x_0) \odot \left[\nabla_ u\right]>\]
$f(X) = g(XW)$, где $X$ и $W$ — матрицы. Как мы знаем,
Здесь через $\ast W$ мы обозначили отображение $Y \hookrightarrow YW$, а в предпоследнем переходе использовалось следующее свойство следа:
где $A, B, C$ — произвольные матрицы подходящих размеров (то есть допускающие перемножение в обоих приведённых порядках). Следовательно, получаем
$f(W) = g(XW)$, где $W$ и $X$ — матрицы. Для приращения $H = W - W_0$ имеем
Здесь через $X \ast$ обозначено отображение $Y \hookrightarrow XY$. Значит,
$f(X) = g(softmax(X))$, где $X$ — матрица $N\times K$, а $softmax$ — функция, которая вычисляется построчно, причём для каждой строки $x$
В этом примере нам будет удобно воспользоваться формализмом с частными производными. Сначала вычислим $\frac<\partial s_l><\partial x_j>$ для одной строки $x$, где через $s_l$ мы для краткости обозначим $softmax(x)_l = \frac> >$. Нетрудно проверить, что
Так как softmax вычисляется независимо от каждой строчки, то
где через $s_$ мы обозначили для краткости $softmax(X)_$.
Теперь пусть $\nabla_ = \nabla g = \frac<\partial\mathcal
Так как $\frac<\partial s_
Таким образом, если мы хотим продифференцировать $f$ в какой-то конкретной точке $X_0$, то, смешивая математические обозначения с нотацией Python, мы можем записать:
Backpropagation в общем виде
Подытожим предыдущее обсуждение, описав алгоритм error backpropagation (алгоритм обратного распространения ошибки). Допустим, у нас есть текущие значения весов $W^i_0$ и мы хотим совершить шаг SGD по мини-батчу $X$. Мы должны сделать следующее:
- Совершить forward pass, вычислив и запомнив все промежуточные представления $X = X^0, X^1, \ldots, X^m = \widehat$.
- Вычислить все градиенты с помощью backward pass.
- С помощью полученных градиентов совершить шаг SGD.
Проиллюстрируем алгоритм на примере двуслойной нейронной сети со скалярным output’ом. Для простоты опустим свободные члены в линейных слоях.

Обучаемые параметры – матрицы $U$ и $W$. Как найти градиенты по ним в точке $U_0, W_0$?
Итого матрица $k\times 1$, как и $W_0$
\[\nabla_\mathcal = \nabla_\left(\vphantom \mathcal\circ h\circ\left[Y\mapsto YW_0\right]\circ g\circ\left[ U\mapsto XU\right] \right)=\] \[=X^T\cdot\nabla_\left(\vphantom\mathcal\circ h\circ [Y\mapsto YW_0]\circ g\right) =\] \[=X^T\cdot\left(\vphantomg'(XU_0)\odot \nabla_\left[\vphantom<\in_0^1>\mathcal\circ h\circ[Y\mapsto YW_0\right] \right)\] \[=\ldots = \underset\cdot\left(\vphantom \underbrace_\odot \underbrace<\left[\vphantom<\int_0^1>\left( \underbrace
Итого $D\times K$, как и $U_0$
Схематически это можно представить следующим образом:
Backpropagation для двуслойной нейронной сети
Если вы не уследили за вычислениями в предыдущем примере, давайте более подробно разберём его чуть более конкретную версию (для $g = h = \sigma$)
Рассмотрим двуслойную нейронную сеть для классификации. Мы уже встречали ее ранее при рассмотрении линейно неразделимой выборки. Предсказания получаются следующим образом:
\[\widehat = \sigma(X^1 W^2) = \sigma\Big(\big(\sigma(X^0 W^1 )\big) W^2 \Big).\]
Пусть $W^1_0$ и $W^2_0$ — текущее приближение матриц весов. Мы хотим совершить шаг по градиенту функции потерь, и для этого мы должны вычислить её градиенты по $W^1$ и $W^2$ в точке $(W^1_0, W^2_0)$.
Прежде всего мы совершаем forward pass, в ходе которого мы должны запомнить все промежуточные представления: $X^1 = X^0 W^1_0$, $X^2 = \sigma(X^0 W^1_0)$, $X^3 = \sigma(X^0 W^1_0) W^2_0$, $X^4 = \sigma(\sigma(X^0 W^1_0) W^2_0) = \widehat$. Они понадобятся нам дальше.
Для полученных предсказаний вычисляется значение функции потерь:
\[l = \mathcal(y, \widehat) = y \log(\widehat) + (1-y) \log(1-\widehat).\]
Дальше мы шаг за шагом будем находить производные по переменным из всё более глубоких слоёв.
Градиент $\mathcal$ по предсказаниям имеет вид
где, напомним, $ \widehat = \sigma(X^3) = \sigma\Big(\big(\sigma(X^0 W^1_0 )\big) W^2_0 \Big)$ (обратите внимание на то, что $W^1_0$ и $W^2_0$ тут именно те, из которых мы делаем градиентный шаг).
Следующий слой — поэлементное взятие $\sigma$. Как мы помним, при переходе через него градиент поэлементно умножается на производную $\sigma$, в которую подставлено предыдущее промежуточное представление:
Следующий слой — умножение на $W^2_0$. В этот момент мы найдём градиент как по $W^2$, так и по $X^2$. При переходе через умножение на матрицу градиент, как мы помним, умножается с той же стороны на транспонированную матрицу, а значит:
Следующий слой — снова взятие $\sigma$.
Наконец, последний слой — это умножение $X^0$ на $W^1_0$. Тут мы дифференцируем только по $W^1$:
Итоговые формулы для градиентов получились страшноватыми, но они были получены друг из друга итеративно с помощью очень простых операций: матричного и поэлементного умножения, в которые порой подставлялись значения заранее вычисленных промежуточных представлений.
Итак, чтобы нейросеть обучалась, достаточно для любого слоя $f^k: X^\mapsto X^k$ с параметрами $W^k$ уметь:
- превращать $\nabla_\mathcal$ в $\nabla__0>\mathcal$ (градиент по выходу в градиент по входу);
- считать градиент по его параметрам $\nabla_\mathcal$.
При этом слою совершенно не надо знать, что происходит вокруг. То есть слой действительно может быть запрограммирован как отдельная сущность, умеющая внутри себя делать forward pass и backward pass, после чего слои механически, как кубики в конструкторе, собираются в большую сеть, которая сможет работать как одно целое.
Более того, во многих случаях авторы библиотек для глубинного обучения уже о вас позаботились и создали средства для автоматического дифференцирования выражений (autograd). Поэтому, программируя нейросеть, вы почти всегда можете думать только о forward-проходе, прямом преобразовании данных, предоставив библиотеке дифференцировать всё самостоятельно. Это делает код нейросетей весьма понятным и выразительным (да, в реальности он тоже бывает большим и страшным, но сравните на досуге код какой-нибудь разухабистой нейросети и код градиентного бустинга на решающих деревьях и почувствуйте разницу).
Метод обратного распространения ошибки позволяет удобно посчитать градиенты, но дальше с ними что-то надо делать, и старый добрый SGD едва ли справится с обучением современной сетки. Так что же делать? О некоторых приёмах мы расскажем в следующей главе.
Применение алгоритма обратного распространения ошибки — один из известных методов, используемых для глубокого обучения нейронных сетей прямого распространения (такие сети ещё называют многослойными персептронами). Этот метод относят к методу обучения с учителем, поэтому требуется задавать в обучающих примерах целевые значения. В этой статье мы рассмотрим, что собой представляет метод обратного распространения ошибки, как он реализуется, каковы его плюсы и минусы.
Сегодня нейронные сети прямого распространения используются для решения множества сложных задач. Если говорить об обучении нейронных сетей методом обратного распространения, то тут пользуются двумя проходами по всем слоям нейросети: прямым и обратным. При выполнении прямого прохода осуществляется подача входного вектора на входной слой сети, после чего происходит распространение по нейронной сети от слоя к слою. В итоге должна осуществляться генерация набора выходных сигналов — именно он, по сути, является реакцией нейронной сети на этот входной образ. При прямом проходе все синаптические веса нейросети фиксированы. При обратном проходе все синаптические веса настраиваются согласно правил коррекции ошибок, когда фактический выход нейронной сети вычитается из желаемого, что приводит к формированию сигнала ошибки. Такой сигнал в дальнейшем распространяется по сети, причём направление распространения обратно направлению синаптических связей. Именно поэтому соответствующий метод и называют алгоритмом с обратно распространённой ошибкой. Синаптические веса настраивают с целью наибольшего приближения выходного сигнала нейронной сети к желаемому.
Общее описание алгоритма обратного распространения ошибки
К примеру, нам надо обучить нейронную сеть по аналогии с той, что представлена на картинке ниже. Естественно, задачу следует выполнить, применяя алгоритм обратного распространения ошибки:


В многослойных персептронах в роли активационной функции обычно применяют сигмоидальную активационную функция, в нашем случае — логистическую. Формула:

Цель обучения сети
Цель обучения нейросети при использовании алгоритма обратного распространения ошибки — это такая подстройка весов нейросети, которая позволит при приложении некоторого множества входов получить требуемое множество выходов нейронов (выходных нейронов). Можно назвать эти множества входов и выходов векторами. В процессе обучения предполагается, что для любого входного вектора существует целевой вектор, парный входному и задающий требуемый выход. Эту пару называют обучающей. Работая с нейросетями, мы обучаем их на многих парах.
Также можно сказать, что алгоритм использует стохастический градиентный спуск и продвигается в многомерном пространстве весов в направлении антиградиента, причём цель — это достижение минимума функции ошибки.
При практическом применении метода обучение продолжают не до максимально точной настройки нейросети на минимум функции ошибки, а пока не будет достигнуто довольно точное его приближение. С одной стороны, это даёт возможность уменьшить количество итераций обучения, с другой — избежать переобучения нейронной сети.
Пошаговая реализация метода обратного распространения ошибки
Необходимо выполнить следующие действия: 1. Инициализировать синаптические веса случайными маленькими значениями. 2. Выбрать из обучающего множества очередную обучающую пару; подать на вход сети входной вектор. 3. Выполнить вычисление выходных значений нейронной сети. 4. Посчитать разность между выходом нейросети и требуемым выходом (речь идёт о целевом векторе обучающей пары). 5. Скорректировать веса сети в целях минимизации ошибки. 6. Повторять для каждого вектора обучающего множества шаги 2-5, пока ошибка обучения нейронной сети на всём множестве не достигнет уровня, который является приемлемым.
Виды обучения сети по методу обратного распространения
Преимущества и недостатки метода
Значение метода обратного распространения
Появление алгоритма стало знаковым событием и положительно отразилось на развитии нейросетей, ведь он реализует эффективный с точки зрения вычислительных процессов способ обучения многослойного персептрона. В то же самое время, было бы неправильным сказать, что алгоритм предлагает наиболее оптимальное решение всех потенциальных проблем. Зато он действительно развеял пессимизм относительно машинного обучения многослойных машин, который воцарился после публикации в 1969 году работы американского учёного с фамилией Минский.
На предыдущих занятиях мы с вами рассматривали НС с выбранными весами, либо устанавливали их, исходя из определенных математических соображений. Это можно сделать, когда сеть относительно небольшая. Но при увеличении числа нейронов и связей, ручной подбор становится попросту невозможным и возникает задача нахождения весовых коэффициентов связей НС. Этот процесс и называют обучением нейронной сети.
Один из распространенных подходов к обучению заключается в последовательном предъявлении НС векторов наблюдений и последующей корректировки весовых коэффициентов так, чтобы выходное значение совпадало с требуемым:
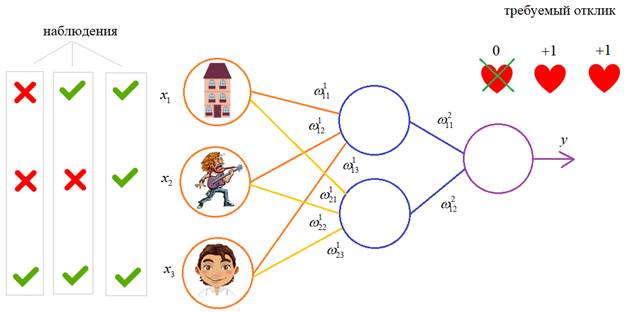
Это называется обучение с учителем, так как для каждого вектора мы знаем нужный ответ и именно его требуем от нашей НС.
Сначала, я думал рассказать о нем со всеми математическими выкладками, но потом решил этого не делать, а просто показать принцип работы и рассмотреть реализацию конкретного примера на Python.

Чтобы все лучше понять, предположим, что у нас имеется вот такая полносвязная НС прямого распространения с весами связей, выбранными произвольным образом в диапазоне от [-0.5; 0,5]. Здесь верхний индекс показывает принадлежность к тому или иному слою сети. Также, каждый нейрон имеет некоторую активационную функцию :
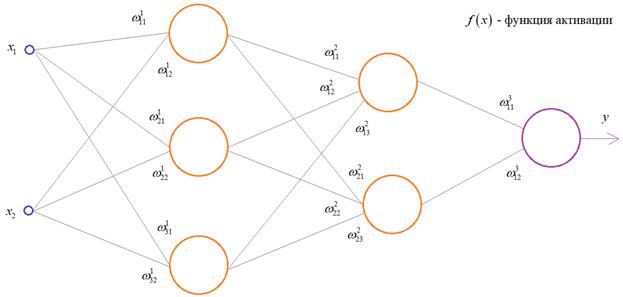

На первом шаге делается прямой проход по сети. Мы пропускаем вектор наблюдения через эту сеть, и запоминаем все выходные значения нейронов скрытых слоев:


и последнее выходное значение y:


Далее, мы знаем требуемый отклик d для текущего вектора , значит для него можно вычислить ошибку работы НС. Она будет равна:

На данный момент все должно быть понятно. Мы на первом занятии подробно рассматривали процесс распространения сигнала по НС. И вы это уже хорошо себе представляете. А вот дальше начинается самое главное – корректировка весов. Для этого делается обратный проход по НС: от последнего слоя – к первому.

Итак, у нас есть ошибка e и некая функция активации нейронов . Первое, что нам нужно – это вычислить локальный градиент для выходного нейрона. Это делается по формуле:

Этот момент требует пояснения. Смотрите, ранее используемая пороговая функция:

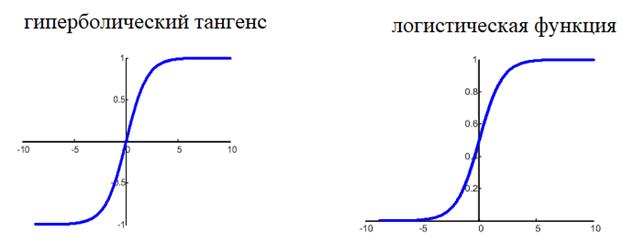
нам уже не подходит, т.к. она не дифференцируема на всем диапазоне значений x. Вместо этого для сетей с небольшим числом слоев, часто применяют или гиперболический тангенс:

или логистическую функцию:

Фактически, они отличаются только тем, что первая дает выходной интервал [-1; 1], а вторая – [0; 1]. И мы уже берем ту, которая нас больше устраивает в данной конкретной ситуации. Например, выберем логистическую функцию.
Ее производная функции по аргументу x дает очень простое выражение:

Именно его мы и запишем в нашу формулу вычисления локального градиента:


то локальный градиент последнего нейрона, равен:


Отлично, это сделали. Теперь у нас есть все, чтобы выполнить коррекцию весов. Начнем со связи , формула будет такой:

Для второй связи все то же самое, только входной сигнал берется от второго нейрона:

Здесь у вас может возникнуть вопрос: что такое параметр λ и где его брать? Он подбирается самостоятельно, вручную самим разработчиком. В самом простом случае можно попробовать следующие значения:

(Мы подробно о нем говорили на занятии по алгоритму градиентного спуска):
Итак, мы с вами скорректировали связи последнего слоя. Если вам все это понятно, значит, вы уже практически поняли весь алгоритм обучения, потому что дальше действуем подобным образом. Переходим к нейрону следующего с конца слоя и для его входящих связей повторим ту же саму процедуру. Но для этого, нужно знать значение его локального градиента. Определяется он просто. Локальный градиент последнего нейрона взвешивается весами входящих в него связей. Полученные значения на каждом нейроне умножаются на производную функции активации, взятую в точках входной суммы:

А дальше действуем по такой же самой схеме, корректируем входные связи по той же формуле:

И для второго нейрона:

Осталось скорректировать веса первого слоя. Снова вычисляем локальные градиенты для нейронов первого слоя, но так как каждый из них имеет два выхода, то сначала вычисляем сумму от каждого выхода:

А затем, значения локальных градиентов на нейронах первого скрытого слоя:

Ну и осталось выполнить коррекцию весов первого слоя все по той же формуле:



В результате, мы выполнили одну итерацию алгоритма обучения НС. На следующей итерации мы должны взять другой входной вектор из нашего обучающего множества. Лучше всего это сделать случайным образом, чтобы не формировались возможные ложные закономерности в последовательности данных при обучении НС. Повторяя много раз этот процесс, весовые связи будут все точнее описывать обучающую выборку.
Отлично, процесс обучения в целом мы рассмотрели. Но какой критерий качества минимизировался алгоритмом градиентного спуска? В действительности, мы стремились получить минимум суммы квадратов ошибок для обучающей выборки:

То есть, с помощью алгоритма градиентного спуска веса корректируются так, чтобы минимизировать этот критерий качества работы НС. Позже мы еще увидим, что на практике используется не только такой, но и другие критерии.
Вот так, в целом выглядит идея работы алгоритма обучения по методу обратного распространения ошибки. Давайте теперь в качестве примера обучим следующую НС:

Итак, сегодня мы продолжим обсуждать тему нейронных сетей на нашем сайте, и, как я и обещал в первой статье (ссылка), речь пойдет об обучении. Тема эта очень важна, поскольку одним из основных свойств нейронных сетей является именно то, что она не только действует в соответствии с каким-то четко заданным алгоритмом, а еще и совершенствуется (обучается) на основе прошлого опыта. И в этой статье мы рассмотрим некоторые формы обучения нейронных сетей, а также несколько практических примеров.
Давайте для начала разберемся, в чем же вообще состоит цель обучения. А все просто - в корректировке весовых коэффициентов связей сети. Одним из самых типичных способов является управляемое обучение. Для его проведения нам необходимо иметь набор входных данных, а также соответствующие им выходные данные. Устанавливаем весовые коэффициенты равными некоторым малым величинам. А дальше процесс протекает следующим образом.
Мы подаем на вход сети данные, после чего сеть вычисляет выходное значение. Мы сравниваем это значение с имеющимся у нас (напоминаю, что для обучения используется готовый набор входных данных, для которых выходной сигнал известен) и в соответствии с разницей между этими значениями корректируем весовые коэффициенты нейронной сети. И эта операция повторяется по кругу много раз. В итоге мы получаем обученную сеть с новыми значениями весовых коэффициентов.
Вроде бы все понятно, кроме того, как именно и по какому алгоритму необходимо изменять значение каждого конкретного весового коэффициента. И в сегодняшней статье для коррекции весов в качестве наглядного примера мы рассмотрим правило Видроу-Хоффа, которое также называют дельта-правилом.
Дельта правило (правило Видроу-Хоффа).
Определим ошибку \delta :
Здесь у нас y_0 - это ожидаемый (истинный) вывод сети, а y - это реальный вывод (активность) выходного элемента. Помимо выходного элемента ошибки можно определить и для всех элементов скрытого слоя нейронной сети, об этом мы поговорим чуть позже.
Дельта-правило заключается в следующем - изменение величины весового коэффициента должно быть равно:
Где \eta - норма обучения. Это число мы сами задаем перед началом обучения. x_j - это сигнал, приходящий к элементу k от элемента j . А \delta_k - ошибка элемента k .
Таким образом, в процессе обучения нейронной сети на вход мы подаем образец за образцом, и в результате получаем новые значения весовых коэффициентов. Обычно обучение заканчивается, когда для всех вводимых образцов величина ошибки станет меньше определенной величины. После этого сеть подвергается тестированию при помощи новых данных, которые не участвовали в обучении. И по результатам этого тестирования уже можно сделать выводы, хорошо или нет справляется сеть со своими задачами.
С корректировкой весов все понятно, осталось определить, каким именно образом и по какому алгоритму будут происходить расчеты при обучении сети. Давайте рассмотрим обучение по алгоритму обратного распространения ошибки.
Алгоритм обратного распространения ошибки.
Итак, для корректировки весовых значений мы будем использовать дельта-правило, которое мы уже обсудили. Вот только необходимо определить универсальное правило для вычисления ошибки каждого элемента сети после, собственно, прохождения через элемент (при обратном распространении ошибки).
Я, пожалуй, не буду приводить математические выводы и расчеты (несмотря на мою любовь к математике), чтобы не перегружать статью, ограничимся только итоговыми результатами )
Функция f(x) - это функция активности элемента. Давайте использовать логистическую функцию, для нее:
Подставляем в предыдущую формулу и получаем величину ошибки:
- \delta_j - ошибка элемента с индексом j
- k - индекс, соответствующий слою, который посылает ошибку "обратно"
- net_j - комбинированный ввод элемента
- f(net_j) - активность элемента
Наверняка сейчас еще все это кажется не совсем понятным, но не переживайте, при рассмотрении практического примера все встанет на свои места! Собственно, давайте к нему и перейдем.
Обучение нейронной сети, практический пример.
Перед обучением сети необходимо задать начальные значения весов - обычно они инициализируются небольшими по величине случайными значениями, к примеру из интервала (-0.5, 0.5). Но для нашего примера возьмем для удобства целые числа.
Рассмотрим нейронную сеть и вручную проведем расчеты для прямого и обратного "потоков" в сети.
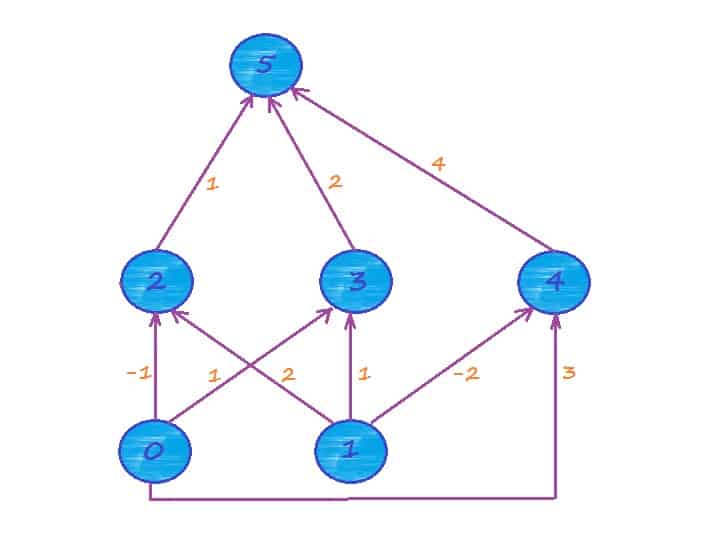
На вход мы должны подать образец, пусть это будет (0.2, 0.5). Ожидаемый выход сети - 0.4. Норма обучения пусть будет равна 0.85. Давайте проведем все расчеты поэтапно. Кстати, совсем забыл, в качестве функции активности мы будем использовать логистическую функцию:
Итак, приступаем. Вычислим комбинированный ввод элементов 2, 3 и 4:
Читайте также:

