Метод координат геометрия 9 класс кратко

Обновлено: 05.07.2024

Основным способом решения задач по стереометрии является метод координат. Освоив его, найти угол между поверхностями или прямыми, расстояние от точки до линии, то есть фактически определить положение объекта не составит труда. Главное достоинство применения этого способа заключается в избавлении от наглядности представления сложных пространственных фигур, что позволяет понять решение даже студенту со слабой математической подготовкой.

Координаты на прямой
Расположение на плоскости
Скалярное произведение
Основные формулы
Нахождение угла
Вычисление площади и высоты
Расчёт на онлайн-калькуляторе

Координаты на прямой

Исследование свойств геометрических тел привело к возникновению отдельной науки — аналитической геометрии. Основополагающим открытием, позволяющим решать задачи, связанные с фигурами, стал координатный метод. В математике принято под координатами понимать положение точки на линии, поверхности или пространстве.

Особенностью способа является нахождение геометрических тел уравнениями. Такой подход позволяет исследовать фигуры и решать задания, взяв за основу алгебраические формулы.

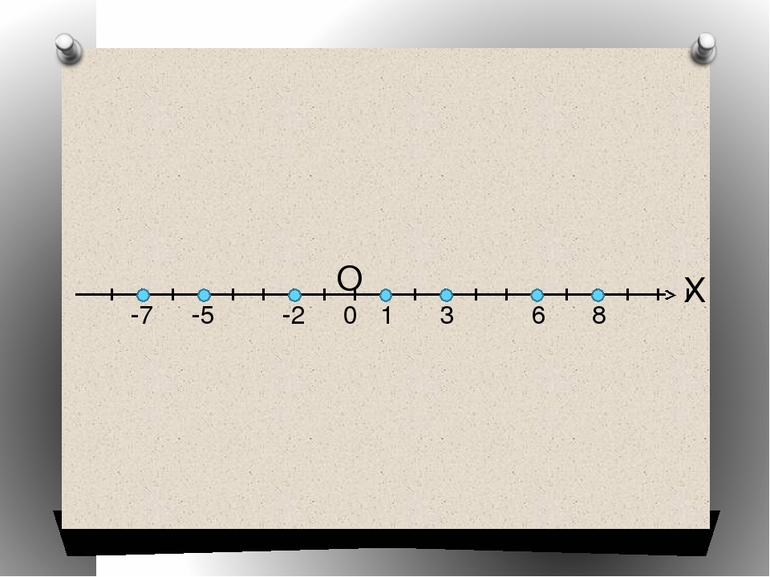
Самая элементарная задача, дающая возможность разобраться в сути, связана с определением положения точки на прямой. Пусть на линии указаны две произвольные точки A и B. Отрезок, который они ограничивают, принимают за единицу длины. Каждой точке P, входящей в AB, соответствует величина, называемая координатой.

Принимать она может три значения:

Положительное. Если P находится на отрезке AP и лежит по ту же сторону от A, что и точка B.
Отрицательное. Если P принадлежит отрезку AP, но при этом точки P и B находятся по разные стороны от B.
Нулевое. Значение координаты точки A равняется нулю.

При выполнении этих условий отрезок называют числовой осью, а A — началом координат. Любая точка, располагающаяся на прямой, имеет свою координату, отличную от других. Но при этом каждое действительное число указывает на расположение точки на рассматриваемой числовой оси. Например, запись вида A (2), B (-¾) обозначает, что числа в скобках являются координатами соответствующих точек.

Расположение на плоскости

Пусть существуют две плоскости, образующие между собой прямой угол. Их точка пересечения A является началом отсчёта любой из них. Если ось одной плоскости обозначить за X, а второй — за Y, то общим для них пространством будет Axy. Ось, совпадающая с X, называется абсциссой, а Y — ординатой. Единица длины для них одинакова. Пересекающиеся оси образуют четверти. Нумерацию принято вести с верхней правой части против часовой стрелки.

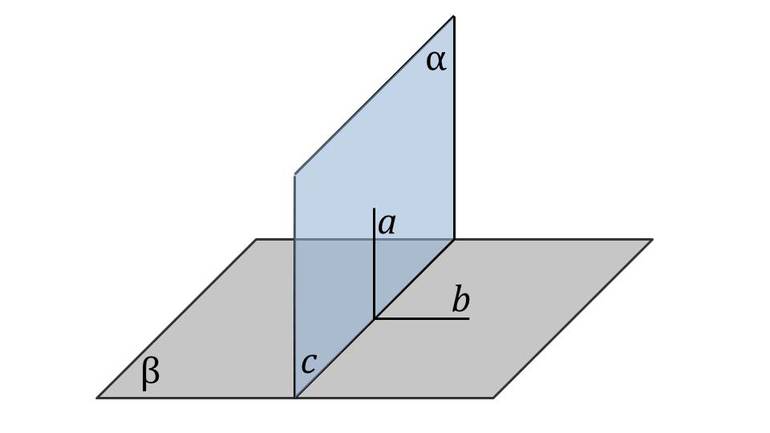
Пусть в плоскости Axy находится произвольная точка. Проведя с неё перпендикуляры на оси, получим два пересечения. Числовые значения в этих местах и будут определять положение A на плоскости, то есть её координаты. Записывают их как A (x, y) и называют декартовыми. Таким образом, нахождение A сводится к определению двух точек, лежащих на осях x и y.

Когда точка располагается на оси X, то её ордината имеет нулевое значение, а если Y — абсцисса. В зависимости от того, в какой четверти находится исследуемый объект, определяется знак его координат. В первой оба числа положительные, а в третьей — отрицательные. Во второй же абсцисса имеет положительное значение, а ордината — отрицательное. В третьей же знаки координат обратные второй четверти.

Естественно, что каждой точке на плоскости соответствует пара чисел. Любая фигура состоит из множества точек. Проведя учёт точек и зная их взаимоотношение относительно друг друга, можно изучить свойство объекта. Эти вычисления позволяет выполнить алгебра и арифметика. Поэтому появляется возможность решать геометрические задачи наглядными алгебраическими способами.

В этом и лежит основа использования метода координат в пространстве. Формулы, применяемые при расчётах, хотя и выглядят устрашающе, на самом деле запоминаются легко. Правда, для этого следует выполнить несколько практических заданий.

Скалярное произведение

Пусть есть два вектора a и b с известными координатами (x1, y1) и (x2, y2). Формула для выражения скалярного произведения векторов через координаты будет иметь вид: a* b = x1*x2 + y1*y2. То есть это сумма произведений соответствующих координат.

Для доказательства следует отложить два вектора из одной точки, направленные в разные стороны. Соединив их конечные точки, можно утверждать, что полученный вектор будет равняться разности a и b. Для образованного треугольника выполняется теорема косинусов: AB 2 = OA 2 + OB 2 — 2*OA*OB * cosα. Так как AB — это всё равно, что длина вектора по модулю в квадрате, то вместо AB можно написать вектор, равный a-b.

В итоге получится: |a-b| 2 = |a| 2 + |b| 2 — 2 |a|*|b|*cosα. Последнее перемножение на косинус по определению является скалярным произведением a и b. Выразив его из выражения, справедливо будет записать: a*b = (|a| 2 + |b| 2 — |a — b| 2 ) /2. Подставив координаты в формулу, получим следующее: a*b = (x1 2 + y1 2 + x2 2 + y2 2 — (x1-x2) 2 + (y1-y2) 2 ) /2 = x1*x2 + y1*y2. Равенство доказано.

Основные формулы

Зачастую в задачах, касающихся расчёта фигур, необходимо посчитать величину отрезка, лежащего на плоскости. Например, это может быть высота, медиана, биссектриса, радиус или сторона. Основной формулой считается выражение, позволяющее найти расстояние между двумя точками. Если даны две координаты A (x1, y1) и B (x2, y2), то искомое значение определяется по формуле: P (A, B) = ((x2-x1) 2 + (y2-y1) 2 ) ½ .

Если же начало отрезка лежит в нулевой точке, то выражение для вычисления его длины упрощается до вида: P (A, B) = ((x) 2 + (y) 2 ) ½ , то есть нахождения суммы квадратов чисел, определяющих координаты. Фактически это теорема Пифагора, изучаемая в шестом классе общеобразовательной школы.

Кроме нахождения длины отрезка, к основным формулам относят:

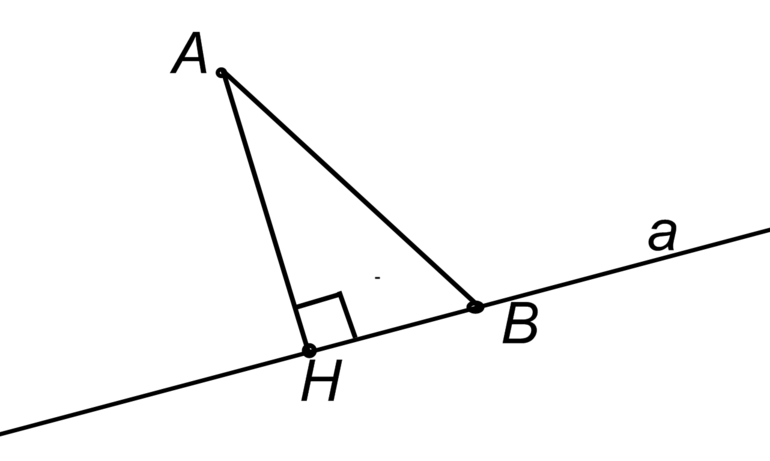
Деление отрезков в заданном отношении. Координату C (xc, yc), образованную из A (x1, y1) и B (x2, y2), определяют из соотношения: AC/CB = α1/α2, где α1,2 — действительные числа. Исходя из этого, Xc = (x1α2 + x2α1) / (α1 + α2), Yc = (y1α2 + y2α1) / (α1 + α2). В основе этих формул используется теорема Фалеса.
Вычисление угла между векторами. Если есть три точки на плоскости A (x1, y1), B (x2, y2), C (x3, y3), то угол между векторами находится как скалярное произведение, делённое на произведение их длин: cosγ = / |AB| * |AC|. Таким образом, если вектор AB = (x2-x1), (y2-y1), а AC (x3-x1, y3-y1), то C = ((x2-x1) * (x3-x1) + (y2-y1) * (y3-y1)) / ((x2-x1) 2 + (y2-y1) 2 ) * ((x3-x1) 2 + (y3-y1) 2 ) ½ .
Уравнение прямой. Для его составления нужна координата точки. Фиксирование положения в пространстве задаётся вектором α, которому рассматриваемая прямая перпендикулярна. Задача, по сути, сводится к написанию уравнения прямой, проходящей через точку N0 (x0, y0), перпендикулярную вектору n (A, B). Формула, удовлетворяющая заданию, имеет вид: A (x-x0) + B (y-y0) = 0. Равенство для прямой, проходящей параллельно вектору, пишется как (x-x0)/a = (y-y0)b. Уравнение же, описывающее прямую, проходящую через две точки, имеет вид: (x-x1)/(x2-x1) = (y-y1)/(y2-y1).

Расстояние от точки до прямой. Если имеется точка (x0, y0) и уравнение: Ax+By+C, то расстояние находится из выражения: |Ax0+Byo+C| / (A 2 +B 2 ) ½ .

Для понимания формул нужно знать о векторном и смешанном произведении векторов, а также об определителе матрицы. Зная их, можно решать задачи по вычислению элементов простейших многогранников, находить площади и объёмы.

Нахождение угла

Например, необходимо найти угол между плоскостями. Координатным методом решить поставленную задачу несложно. С точки зрения геометрии, это угол между двумя параллелями. Отметив на поверхности начало координат, через него можно провести перпендикуляры обеим плоскостям. Образованный угол и будет искомым. Поэтому для решения задачи необходимо:

записать уравнения плоскостей;
составить векторы нормали;
вычислить значение косинуса угла между поверхностями.

Для составления уравнений следует найти положение трёх точек, лежащих в плоскости, но не на одной нормали. Затем каждое из них подставить в уравнение и получить систему. Решается последняя любым доступным методом, например, нахождением определителя матрицы или графическим смешанным методом. В итоге находят корни системы A, B, C и составляют вектор нормали. При этом полученные координаты не должны быть коллинеарными, то есть не лежать на одной прямой или быть параллельными.

Пусть имеется единичный куб, в котором нужно найти угол, образованный A1, B1, C1 и C1, D, A1. Вначале определяют координаты первой плоскости и подставляют их в уравнение: Ax+By+Cz+1 = 0. Тут следует отметить: свободный член добавляется из-за того, что поверхности не проходят через середину координат. Точки определяются значениями: A1 (1, 0, 1), B (0,0,1), D (1,1,0). После подстановки система уравнений примет вид:

Из второго равенства можно определить C. Подставив найденное C в первое равенство, можно выразить A, а после найти B. Таким образом, решением системы будет A = 0, B = -1, C = -1. Вектор нормали, соответственно, будет: N1 (0; -1; -1).

Чтобы составить уравнение второй плоскости, нужно найти координаты лишь С1. Исходя из условия, они будут равны С1 (0; 1; 1), а A и D уже известны. Подставляя данные в уравнение Ax+By+Cz+1 = 0, опять составляют систему и находят её коэффициенты. После решения второй матрицы, например, методом разложения, можно записать координаты второго вектора: N2 (-½; ½; -½).

Теперь, когда известны N1 и N2, нужно найти косинус между ними, являющийся углом двух искомых плоскостей. Используя формулу для вычисления угла векторов, можно получить следующее: cosα = |½ + ½| / (2 ½ * ¾ ½ ) = 1 / (6 ½ /2) = 2/6 ½ = 6 ½ / 3. Соответственно, угол равен: α = arccos = 6 ½ / 3.

Вычисление площади и высоты

Рассмотрим типовую задачу, встречающуюся в экзаменационных работах. Даны точки с ординатами A (-2, -3); B (-3,4); C (4,5). Необходимо выполнить построение фигуры, найти её площадь и доказать, что угол A равный C.

Если отложить данные точки на плоскости и соединить их, то получится треугольник. Взяв за тождество, что углы A и C равны, можно сделать предположение о равнобедренности треугольника. Это значит, что две его стороны имеют одинаковую длину. Длина стороны AB — это отрезок A и B с заданными координатами. Поэтому равна она будет следующему выражению: AB = ((-2 + 3) 2 + (-3 — 4) 2 ) ½ = (1 +49) ½ = (50) ½ . По аналогии находится длина другой стороны: BC = ((-3 — 4) 2 + (4 — 5) 2 ) ½ = 2 = (1 +49) ½ = (50) ½ .

Таким образом, у треугольника две стороны равны, а значит, он равнобедренный. У найденных сторон общей точкой является B (вершина). Следовательно, углы A и C будут равны. Что и требовалось доказать.

Для того чтобы найти площадь треугольника, используется правило, что она находится умножением высоты на длину стороны, к которой проведена, и делением полученного результата на два: S = h*a/2 = BH * AC /2, где H — точка пересечения высоты и основания.

В равнобедренном треугольнике высота является биссектрисой и медианой, поэтому H лежит на середине отрезка AC. Чтобы найти её положение, используют формулу нахождения координат середины отрезка: H (x, y): X = (-2+4) /2 = 1, Y = (-3+5) / 2 = 1. Искомая точка имеет координаты H (1,1).

Высота находится как корень квадратный из двух точек: BH = ((-3−1) 2 + (4−1) 2 ) ½ = (16+9) ½ = 5. Теперь нужно найти основание треугольника AC. Разницы, из какой координаты вычитать другую, нет, так как результат учитывается по модулю. Основание будет равно: AC = ((-2−4) 2 + (-3−5) 2 ) ½ = (36 + 64) ½ = 10. Полученные значения высоты и основания подставляют в формулу нахождения площади и получают, что она равна: S = 5*10/2 = 25. Задача решена.

Расчёт на онлайн-калькуляторе

Существуют сервисы, позволяющие решать геометрические задачи координатным методом без утомительных самостоятельных вычислений. Сам расчёт обычно занимает не более трёх секунд, а за достоверность результата можно не беспокоиться.

Воспользоваться услугами таких сайтов сможет любой пользователь интернета, даже не имеющий представления о геометрии. Всё, что от него требуется — это подключение к сети и веб-обозреватель с поддержкой Flash-технологии.

Для того, чтобы использовать метод координат, надо хорошо знать формулы. Их три:

Главная формула — косинус угла φ между векторами a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂):

На первый взгляд, выглядит угрожающе, но достаточно немного практики — и все будет работать великолепно.

Задача. Найти косинус угла между векторами a = (4; 3; 0) и b = (0; 12; 5).

Решение. Поскольку координаты векторов нам даны, подставляем их в первую формулу:

Задача. Составить уравнение плоскости, проходящей через точки M = (2; 0; 1), N = (0; 1; 1) и K = (2; 1; 0), если известно, что она не проходит через начало координат.

Решение. Общее уравнение плоскости: Ax + By + Cz + D = 0, но, поскольку искомая плоскость не проходит через начало координат — точку (0; 0; 0) — то положим D = 1. Поскольку эта плоскость проходит через точки M, N и K, то координаты этих точек должны обращать уравнение в верное числовое равенство.

Подставим вместо x, y и z координаты точки M = (2; 0; 1). Имеем:
A · 2 + B · 0 + C · 1 + 1 = 0 ⇒ 2A + C + 1 = 0;

Аналогично, для точек N = (0; 1; 1) и K = (2; 1; 0) получим уравнения:
A · 0 + B · 1 + C · 1 + 1 = 0 ⇒ B + C + 1 = 0;
A · 2 + B · 1 + C · 0 + 1 = 0 ⇒ 2A + B + 1 = 0;

Итак, у нас есть три уравнения и три неизвестных. Составим и решим систему уравнений:

Получили, что уравнение плоскости имеет вид: − 0,25x − 0,5y − 0,5z + 1 = 0.

Задача. Плоскость задана уравнением 7x − 2y + 4z + 1 = 0. Найти координаты вектора, перпендикулярного данной плоскости.

Решение. Используя третью формулу, получаем n = (7; − 2; 4) — вот и все!

Вычисление координат векторов

А что, если в задаче нет векторов — есть только точки, лежащие на прямых, и требуется вычислить угол между этими прямыми? Все просто: зная координаты точек — начала и конца вектора — можно вычислить координаты самого вектора.

Чтобы найти координаты вектора, надо из координат его конца вычесть координаты начала.

Задача. В пространстве расположены три точки, заданные своими координатами: A = (1; 6; 3), B = (3; − 1; 7) и C = (− 4; 3; − 2). Найти координаты векторов AB, AC и BC.

Рассмотрим вектор AB: его начало находится в точке A, а конец — в точке B. Следовательно, чтобы найти его координаты, надо из координат точки B вычесть координаты точки A:
AB = (3 − 1; − 1 − 6; 7 − 3) = (2; − 7; 4).

Аналогично, начало вектора AC — все та же точка A, зато конец — точка C. Поэтому имеем:
AC = (− 4 − 1; 3 − 6; − 2 − 3) = (− 5; − 3; − 5).

Наконец, чтобы найти координаты вектора BC, надо из координат точки C вычесть координаты точки B:
BC = (− 4 − 3; 3 − (− 1); − 2 − 7) = (− 7; 4; − 9).

Ответ: AB = (2; − 7; 4); AC = (− 5; − 3; − 5); BC = (− 7; 4; − 9)

Обратите внимание на вычисление координат последнего вектора BC: очень многие ошибаются, когда работают с отрицательными числами. Это касается переменной y: у точки B координата y = − 1, а у точки C y = 3. Получаем именно 3 − (− 1) = 4, а не 3 − 1, как многие считают. Не допускайте таких глупых ошибок!

Вычисление направляющих векторов для прямых

Если вы внимательно прочитаете задачу C2, то с удивлением обнаружите, что никаких векторов там нет. Там только прямые да плоскости.

Для начала разберемся с прямыми. Здесь все просто: на любой прямой найдутся хотя бы две различные точки и, наоборот, любые две различные точки задают единственную прямую.

Кто-нибудь понял, что написано в предыдущем абзаце? Я и сам не понял, поэтому объясню проще: в задаче C2 прямые всегда задаются парой точек. Если ввести систему координат и рассмотреть вектор с началом и концом в этих точках, получим так называемый для прямой:

Зачем нужен этот вектор? Дело в том, что — это угол между их направляющими векторами. Таким образом, мы переходим от непонятных прямых к конкретным векторам, координаты которых легко считаются. Насколько легко? Взгляните на примеры:

Задача. В кубе ABCDA₁B₁C₁D₁ проведены прямые AC и BD₁. Найдите координаты направляющих векторов этих прямых.

Поскольку длина ребер куба в условии не указана, положим AB = 1. Введем систему координат с началом в точке A и осями x, y, z, направленными вдоль прямых AB, AD и AA₁ соответственно. Единичный отрезок равен AB = 1.

Теперь найдем координаты направляющего вектора для прямой AC. Нам потребуются две точки: A = (0; 0; 0) и C = (1; 1; 0). Отсюда получаем координаты вектора AC = (1 − 0; 1 − 0; 0 − 0) = (1; 1; 0) — это и есть направляющий вектор.

Теперь разберемся с прямой BD₁. На ней также есть две точки: B = (1; 0; 0) и D₁ = (0; 1; 1). Получаем направляющий вектор BD₁ = (0 − 1; 1 − 0; 1 − 0) = (− 1; 1; 1).

Ответ: AC = (1; 1; 0); BD₁ = (− 1; 1; 1)

Задача. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, проведены прямые AB₁ и AC₁. Найдите координаты направляющих векторов этих прямых.

Введем систему координат: начало в точке A, ось x совпадает с AB, ось z совпадает с AA₁, ось y образует с осью x плоскость OXY, которая совпадает с плоскостью ABC.

Для начала разберемся с прямой AB₁. Тут все просто: у нас есть точки A = (0; 0; 0) и B₁ = (1; 0; 1). Получаем направляющий вектор AB₁ = (1 − 0; 0 − 0; 1 − 0) = (1; 0; 1).

Теперь найдем направляющий вектор для AC₁. Все то же самое — единственное отличие в том, что у точки C₁ иррациональные координаты. Итак, A = (0; 0; 0), поэтому имеем:

Небольшое, но очень важное замечание насчет последнего примера. Если начало вектора совпадает с началом координат, вычисления резко упрощаются: координаты вектора просто равны координатам конца. К сожалению, это верно лишь для векторов. Например, при работе с плоскостями присутствие на них начала координат только усложняет выкладки.

Вычисление нормальных векторов для плоскостей

Нормальные векторы — это не те векторы, у которых все в порядке, или которые чувствуют себя хорошо. По определению, нормальный вектор (нормаль) к плоскости — это вектор, перпендикулярный данной плоскости.

Другими словами, — это вектор, перпендикулярный любому вектору в данной плоскости. Наверняка вы встречали такое определение — правда, вместо векторов речь шла о прямых. Однако чуть выше было показано, что в задаче C2 можно оперировать любым удобным объектом — хоть прямой, хоть вектором.

Еще раз напомню, что всякая плоскость задается в пространстве уравнением Ax + By + Cz + D = 0, где A, B, C и D — некоторые коэффициенты. Не умаляя общности решения, можно полагать D = 1, если плоскость не проходит через начало координат, или D = 0, если все-таки проходит. В любом случае, координаты нормального вектора к этой плоскости равны n = (A; B; C).

Итак, плоскость тоже можно успешно заменить вектором — той самой нормалью. Всякая плоскость задается в пространстве тремя точками. Как найти уравнение плоскости (а следовательно — и нормали), мы уже обсуждали в самом начале статьи. Однако этот процесс у многих вызывает проблемы, поэтому приведу еще парочку примеров:

Задача. В кубе ABCDA₁B₁C₁D₁ проведено сечение A₁BC₁. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA₁ соответственно.

Поскольку плоскость не проходит через начало координат, ее уравнение выглядит так: Ax + By + Cz + 1 = 0, т.е. коэффициент D = 1. Поскольку эта плоскость проходит через точки A₁, B и C₁, то координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 + 1 = 0 ⇒ C + 1 = 0 ⇒ C = − 1;

Аналогично, для точек B = (1; 0; 0) и C₁ = (1; 1; 1) получим уравнения:
A · 1 + B · 0 + C · 0 + 1 = 0 ⇒ A + 1 = 0 ⇒ A = − 1;
A · 1 + B · 1 + C · 1 + 1 = 0 ⇒ A + B + C + 1 = 0;

Но коэффициенты A = − 1 и C = − 1 нам уже известны, поэтому остается найти коэффициент B:
B = − 1 − A − C = − 1 + 1 + 1 = 1.

Получаем уравнение плоскости: − A + B − C + 1 = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; − 1).

Задача. В кубе ABCDA₁B₁C₁D₁ проведено сечение AA₁C₁C. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA₁ соответственно.

В данном случае плоскость проходит через начало координат, поэтому коэффициент D = 0, а уравнение плоскости выглядит так: Ax + By + Cz = 0. Поскольку плоскость проходит через точки A₁ и C, координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 = 0 ⇒ C = 0;

Аналогично, для точки C = (1; 1; 0) получим уравнение:
A · 1 + B · 1 + C · 0 = 0 ⇒ A + B = 0 ⇒ A = − B;

Положим B = 1. Тогда A = − B = − 1, и уравнение всей плоскости имеет вид: − A + B = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; 0).

Вообще говоря, в приведенных задачах надо составлять систему уравнений и решать ее. Получится три уравнения и три переменных, но во втором случае одна из них будет свободной, т.е. принимать произвольные значения. Именно поэтому мы вправе положить B = 1 — без ущерба для общности решения и правильности ответа.

Координаты середины отрезка

Очень часто в задаче C2 требуется работать с точками, которые делят отрезок пополам. Координаты таких точек легко считаются, если известны координаты концов отрезка.

Итак, пусть отрезок задан своими концами — точками A = (x_a; y_a; z_a) и B = (x_b; y_b; z_b). Тогда координаты середины отрезка — обозначим ее точкой H — можно найти по формуле:

Другими словами, координаты середины отрезка — это среднее арифметическое координат его концов.

Задача. Единичный куб ABCDA₁B₁C₁D₁ помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA₁ соответственно, а начало координат совпадает с точкой A. Точка K — середина ребра A₁B₁. Найдите координаты этой точки.

Поскольку точка K — середина отрезка A₁B₁, ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A₁ = (0; 0; 1) и B₁ = (1; 0; 1). Теперь найдем координаты точки K:

Задача. Единичный куб ABCDA₁B₁C₁D₁ помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA₁ соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A₁B₁C₁D₁.

Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A₁L = C₁L, т.е. точка L — это середина отрезка A₁C₁. Но A₁ = (0; 0; 1), C₁ = (1; 1; 1), поэтому имеем:

Основные сведения о координатах вектора (напоминание)

Любой вектор разлагается по векторам и однозначно:

Если известно начало вектора – точка и конец вектора – точка то координаты вектора то есть из координат конца нужно вычесть координаты начала.

Через координаты векторов мы умеем находить их сумму, разность и произведение на число.

Пользуясь всем этим, рассмотрим три опорные задачи:

Координаты середины отрезка

Задача 1. Координаты середины отрезка.

Дано: отрезок АВ; ; ; С – середина АВ.

Найти: координаты точки .

Рис. 1. Иллюстрация к задаче

Построим векторы , и .

Найдем вектор :

Так как С – середина отрезка и векторы и противонаправлены, то , следовательно .

Найдем координаты вектора

Координаты вектора совпадают с координатами точки , координаты вектора совпадают с координатами точки .

Координаты вектора совпадают с координатами точки , следовательно

Определение длины вектора

Задача 2. Вычисление длины вектора по его координатам.

Дано: вектор

Найти: длину вектора .

Рис. 2. Иллюстрация к задаче

Задан вектор , отложим его от начала координат, получим вектор с началом в точке и концом в точке .

это проекция на ось ;

это проекция на ось

По теореме Пифагора

Если вектор задан своими координатами, то его длина находится по формуле:

Формула расстояния между точками

Задача 3. Вычисление расстояния между точками.

Дано: точки и .

Найти: расстояние между точками.

Рис. 3. Иллюстрация к задаче

Рассмотрим вектор . Из координат конца вычтем координаты начала:

Теперь нужно найти длину этого вектора.

Для этого отложим его от начала координат (рис. 4).

Рис. 4. Иллюстрация к задаче

Получаем точки и

;

Раз векторы равны, то координаты точки ( равны координатам вектора .

(По формуле, полученной в задаче 2).

Решение задач

Дано: отрезок , точка и точка середина .

Найти: координаты точки .

Рис. 5. Иллюстрация к задаче

Каждая координата точки равна полусумме соответствующих координат точек

Находим :

Ответ:

Дано: .

Найти: расстояние =

Рис. 6. Иллюстрация к задаче

Ответ:

Обзор основных сведений и формул для векторов в координатах

В координатной плоскости любой вектор однозначно разлагается по векторам и

Числа определяются единственным образом и называются координатами вектора в данной системе координат (рис. 1).

Рис. 1. Координаты вектора

Если есть точка , то вектор с началом в начале координат, который называется радиус-вектором точки , имеет те же самые координаты: .

Основываясь на этом, мы рассмотрели 3 стандартные задачи:

Определение координат середины отрезка по координатам концов отрезка и

Рис. 2. Иллюстрация к задаче

Определение длины вектора с координатами .

Определение длины отрезка по координатам концов и .

Теперь применим эти сведения для решения задач.

Решение задач с использованием метода координат

Рис. 3. Иллюстрация к задаче

Дан треугольник с вершинами . Найти медиану .

Дано:

;

Найти: .

Найдем координаты точки как середины отрезка ВС:

Найдем длину отрезка :

Ответ: .

Вершина параллелограмма лежит на положительной полуоси , вершина имеет координаты ; . Найти координаты точки сторону диагональ .

Построим данный параллелограмм в прямоугольной системе координат (рис. 4).

Рис. 4. Иллюстрация к задаче

Так как , то координаты точки . Пусть координаты точки .

Так как параллелограмм, то ;

Координаты равны, следовательно,

Итак, ;

так как вектор имеет те же координаты, что и точка .

так как координаты вектора совпадают с координатами точки

Ответ: ;

Найти периметр треугольника, если известны координаты его вершин (рис. 5).

Рис. 5. Иллюстрация к задаче

Дано:

;

Найти: периметр .

Воспользуемся формулой вычисления расстояния между точками.

Найдем длину :

Ответ:

Заключение

Итак, мы рассмотрели три простейшие опорные задачи и применили их для решения конкретных примеров.

Мы сделали обзор сведений о координатах, о простейших задачах и применили эти сведения для решения конкретных геометрических задач

Метод координат - это подход к изучению свойств геометрических фигур, используя методы алгебры.

Задачи

1. Координаты середины отрезка.

Дано: система координат , А(₁; ₁), В(₂; ₂), С середина отрезка АВ.

Выразить: координаты С(; ) через координаты концов отрезка АВ.

Решение:

С - середина отрезка АВ, поэтому . (1)

(Доказательство утверждения (1) приведено в разделе "Применение векторов к решению задач").

Координаты векторов , и равны соответствующим координатам точек С, А и В:

, и .

Записывая равенство (1) в координатах, получим:

, следовательно, и .

Каждая координата середины отрезка равна полусумме соответствующих координат его концов.

2. Вычисление длины вектора по его координатам.

Дано: .

Доказать: .

Доказательство:

1. и .

Отложим от начала координат вектор и проведем через точку А перпендикуляры АА₁ и АА₂ к осям и .

Координаты точки А равны координатам вектора , т.е. (; ). Поэтому . По теореме Пифагора: .

Но , следовательно, . Что и требовалось доказать.

2. и .

Отложим от начала координат вектор , учитывая то, что .

Но , следовательно, . Что и требовалось доказать.

3. и .

Отложим от начала координат вектор , учитывая то, что .

Но , следовательно, . Что и требовалось доказать.

Длина вектора равна квадратному корню из суммы квадратов координат данного вектора.

3. Расстояние между двумя точками.

Дано: М₁(₁; ₁), М₂(₂; ₂), - расстояние между М₁ и М₂.

Выразить: через координаты М₁ и М₂.

Решение:

Рассмотрим вектор , каждая его координата равна разности соответствующих координат его конца и начала, т.е. . Следовательно, длина этого вектора: .

Но , значит, расстояние между точками М₁(₁; ₁) и М₂(₂; ₂) выражается формулой:

Читайте также: