Метод дихотомии теория кратко

Обновлено: 04.07.2024

Содержание

Пример

Преимущества и недостатки

Дихотомическое деление привлекательно своей простотой. Действительно, при дихотомии мы всегда имеем дело лишь с двумя классами, которые исчерпывают объем делимого понятия. Таким образом, дихотомическое деление всегда соразмерно; члены деления исключают друг друга, так как каждый объект делимого множества попадает только в один из классов а или не а; деление проводится по одному основанию — наличие или отсутствие некоторого признака. Обозначив делимое понятие буквой а и выделив в его объёме некоторый вид, скажем, b, можно разделить объем а на две части — b и не b.

Применение

Дихотомия обычно используется как вспомогательный приём при установлении классификации.

Также она известна благодаря достаточно широко используемому методу поиска, так называемому методу дихотомии. Он применяется для нахождения значений действительно-значной функции, определяемому по какому-либо критерию (это может быть сравнение на минимум, максимум или конкретное число). Рассмотрим метод дихотомии условной одномерной оптимизации (для определённости минимизации).

Метод дихотомии

Метод дихотомии несколько схож с методом двоичного поиска, однако отличается от него критерием отбрасывания концов.

$f(x):\;[a,\;b]\to\mathrm<R> Пускай задана функция ,\;f(x)\in\mathrm([a,\;b])\!$
.

Разобьём мысленно заданный отрезок пополам и возьмём две симметричные относительно центра точки и так, что:

$\begin x_1 &=& \frac-\delta\\ x_2 &=& \frac+\delta \end\!$
,

где — некоторое число в интервале \right)\!" width="" height="" />

Отбросим тот из концов изначального интервала, к которому ближе оказалась одна из двух вновь поставленных точек с максимальным значением (напомним, мы ищем минимум), то есть:

Процедура повторяется пока не будет достигнута заданная точность, к примеру, пока длина отрезка не достигнет удвоенного значения заданной погрешности.

$\delta=(b-a)\left(\frac На каждой итерации приходится вычислять новые точки. Можно добиться того, чтобы на очередной итерации было необходим высчитывать лишь одну новую точку, что заметно способствовало бы оптимизации процедуры. Это достигается путём зеркального деления отрезка в золотом сечении, в этом смысле метод золотого сечения можно рассматривать, как улучшение метода дихотомии с параметром -\frac<\phi>\right)\!$
.

Метод дихотомии имеет свое название от древнегреческого слова , что в переводе означает деление надвое. Именно поэтому данные метод имеет еще второе название: метод половинного деления. Его мы используем довольно часто. Допустим, играя в игру "Угадай число", где один игрок загадывает число от 1 до 100, а другой пытается его отгадать, руководствуясь подсказками "больше" или "меньше". Логично предположить, что первым числом будет названо 50, а вторым в случае если оно меньше - 25, если больше - 75. Таким образом, на каждом этапе (иттерации) неопределенность неизвестного уменьшается в 2 раза. Т.е. даже самый невезучий в мире человек отгадает загаданное число в данном диапазоне за 7 предположений вместо 100 случайных утверждений.

Метод половинного деления в решении уравнения

Правильное решение уравнения методом половинного деления возможно лишь в том случае, если известно, что на заданном интервале имеется корень и он является единственным. Это совсем не означает что метод дихотомии может использоваться только для решения линейных уравнений. Для нахождения корней уравнений более высокого порядка методом половинного деления необходимо сначала отделить корни по отрезкам. Процесс отделения корней осуществляется путем отыскания первой и второй производной от функции и приравнивании их нулю f'(x)=0 и f''(x)=0. Далее определяются знаки f(x) в критических и граничных точках. Интервал, где функция меняет знак |a,b|, где f(a)*f(b) 3 -3*x+1=0 с точностью в 10 -3

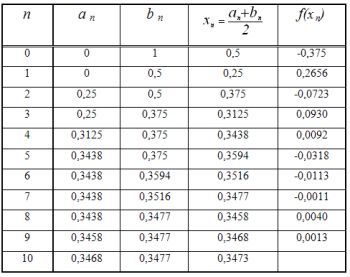
Как видно из таблицы корнем является 0,347. Колличество иттераций равно 10. Условие завершения: a-b=0,0009 -3

Метод половинного деления или метод дихотомии является наиболее простым для решения уравнения в численных методах.

Решение уравнения методом дихотомии - Решение уравнения методом половинного деления в Паскале.

Приближенные значения корней уточняют различными итерационными методами, наиболее эффективными из которых являются метод дихотомии, метод Ньютона, метод секущих.

Метод дихотомии

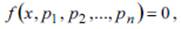
Во многих научных и инженерных задачах возникает необходимость решения уравнений вида (1)

где f – заданная функция;

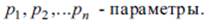
x – неизвестная переменная;

Считаем, что в уравнении (1) отделение корней проведено и на отрезке [a,b] расположен только один корень (рис. 1.1.).

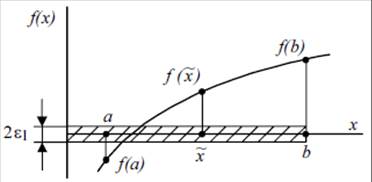
Рисунок 1.1. Метод дихотомии

Суть метода дихотомии заключается в следующем:

Делят интервал [a,b] пополам и находят

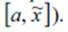
Корень будет находиться в той половине отрезка, на концах которой функция f (x) имеет разные знаки (в нашем случае это интервал

Следовательно, для следующего шага уточнения корня точку b нужно переместить в середину отрезка, т.е. положить , и продолжить процесс до тех пор, пока не будет выполняться условие

Алгоритм метода дихотомии состоит из

1. Ввод интервала [a,b], требуемой погрешности вычисления корня ε, полосы шума 2ε₁ .

2. Нахождение средней точки интервала:

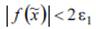
3. Проверка условия и прекращение итерационного процесса (переход к п. 8) в случае его выполнения.

4. Определение знака функции f(x) в средней точке и в точке их сравнение.

5. В случае совпадения знаков перенос точки a в точку , в противном случае перенос точки b в точку

6. Проверка условия и прекращение итерационного процесса (переход к п. 8) в случае его выполнения.

7. В противном случае возвращение к п. 2 и продолжение вычислений.

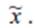
8. Вывод уточненного значения корня

Преимуществами метода дихотомии являются его простота, надежность, сходимость к простому корню для любых, в т.ч. недифференцируемых функций. К его недостаткам следует отнести относительно невысокую скорость сходимости и необходимость предварительного определения интервала, на котором функция меняет знак. Метод применяется главным образом в тех случаях, когда требуется высокая надежность счета, а скорость сходимости малосущественна.

Метод половинного деления (дихотомии, бисекции, вилки, проб) отличается от большинства методов тем, что для его сходимости не требуется, чтобы функция f(x) была дифференцируемой, достаточно непрерывности f(x).

Пусть корень уравнения отделен, т.е. имеем, что f(a) и f(b) разных знаков: f(a)∙f(b)

Аналогичная операция производится для остальных значений у.

Метод Рунге-Кутта

Метод Рунге-Кутта является более точным по сравнению с методом Эйлера.

Суть уточнения состоит в том, что искомое решение представляется в виде разложения в ряд Тейлора.

Если в этой формуле ограничиться двумя первыми слагаемыми, то получим формулу метода Эйлера. Метод Рунге-Кутта учитывает четыре первых члена разложения.

В методе Рунге-Кутта приращения Dy_i предлагается вычислять по формуле:

где коэффициенты k_i вычисляются по формулам:

Контрольные вопросы

2. Метод Рунге - Кутта

Пусть корень уравнения отделен, т.е. имеем, что f(a) и f(b) разных знаков: f(a)∙f(b)

Метод Рунге-Кутта

Метод Рунге-Кутта является более точным по сравнению с методом Эйлера.

Суть уточнения состоит в том, что искомое решение представляется в виде разложения в ряд Тейлора.

В методе Рунге-Кутта приращения Dy_i предлагается вычислять по формуле:

Читайте также: