Интегрирование тригонометрических функций теория кратко

Обновлено: 04.07.2024

На практике часто приходится вычислять интегралы трансцендентных функций, которые содержат тригонометрические функции. В рамках этого материала мы опишем основные виды подынтегральных функций и покажем, какие методы можно использовать для их интегрирования.

Интегрирование синуса, косинуса, тангенса и котангенса

Начнем с методов интегрирования основных тригонометрических функций – sin , cos , t g , c t g . Используя таблицу первообразных, сразу запишем, что ∫ sin x d x = - cos x + C , а ∫ cos x d x = sin x + C .

Для вычисления неопределенных интегралов функций t g и c t g можно воспользоваться подведением под знак дифференциала:

∫ t g x d x = ∫ sin x cos x d x = d ( cos x ) = - sin x d x = = - ∫ d ( cos x ) cos x = - ln cos x + C ∫ c t g x d x = ∫ cos x sin x d x = d ( sin x ) = cos x d x = = ∫ d ( sin x ) sin x = ln sin x + C

Как же у нас получились формулы ∫ d x sin x = ln 1 - cos x sin x + C и ∫ d x cos x = ln 1 + sin x cos x + C , взятые из таблицы первообразных? Поясним только один случай, поскольку второй будет понятен по аналогии.

Используя метод подстановки, запишем:

∫ d x sin x = sin x = t ⇒ x = a r c sin y ⇒ d x = d t 1 - t 2 = d t t 1 - t 2

Здесь нам нужно интегрировать иррациональную функцию. Берем тот же метод подстановки:

∫ d t t 1 - t 2 = 1 - t 2 = z 2 ⇒ t = 1 - z 2 ⇒ d t = - z d z 1 - z 2 = = ∫ - z d z z 1 - z 2 · 1 - z 2 = ∫ d z z 2 - 1 = ∫ d z ( z - 1 ) ( z + ) = = 1 2 ∫ d z z - 1 - 1 2 ∫ d z z + 1 = 1 2 ln z - 1 - 1 2 z + 1 + C = = 1 2 ln z - 1 z + 1 + C = ln z - 1 z + 1 + C

Теперь производим обратную замену z = 1 - t 2 и t = sin x :

∫ d x sin x = ∫ d t t 1 - t 2 = ln z - 1 z + 1 + C = = ln 1 - t 2 - 1 1 - t 2 + 1 + C = ln 1 - sin 2 x - 1 1 - sin 2 x + 1 + C = = ln cos x - 1 cos x + 1 + C = ln ( cos x - 1 ) 2 sin 2 x + C = = ln cos x - 1 sin x + C

Отдельно разберем случаи с интегралами, которые содержат степени тригонометрических функций, таких, как ∫ sin n x d x , ∫ cos n x d x , ∫ d x sin n x , ∫ d x cos n x .

О том, как их правильно вычислять, можно прочесть в статье об интегрировании с использованием рекуррентных формул. Если вы знаете, каким образом выведены эти формулы, то легко сможете брать интегралы вроде ∫ sin n x · cos m x d x с натуральными m и n .

Если у нас имеется комбинация тригонометрических функций с многочленами или показательными функциями, то их придется интегрировать по частям. Советуем прочесть статью, посвященную методам нахождения интегралов ∫ P n ( x ) · sin ( a x ) d x , ∫ P n ( x ) · cos ( a x ) d x , ∫ e a · x · sin ( a x ) d x , ∫ e a · x · cos ( a x ) d x .

Наиболее сложными являются задачи, в которых подынтегральная функция включает в себя тригонометрические функции с разными аргументами. Для этого нужно пользоваться основными формулами тригонометрии, так что желательно помнить их наизусть или держать запись под рукой.

Найдите множество первообразных функции y = sin ( 4 x ) + 2 cos 2 ( 2 x ) sin x · cos ( 3 x ) + 2 cos 2 x 2 - 1 · sin ( 3 x ) .

Решение

Воспользуемся формулами понижения степени и запишем, что cos 2 x 2 = 1 + cos x 2 , а cos 2 2 x = 1 + cos 4 x 2 . Значит,

y = sin ( 4 x ) + 2 cos 2 ( 2 x ) sin x · cos ( 3 x ) + 2 cos 2 x 2 - 1 · sin ( 3 x ) = sin ( 4 x ) + 2 · 1 + cos 4 x 2 sin x · cos ( 3 x ) + 2 · 1 + cos x 2 - 1 · sin ( 3 x ) = = sin ( 4 x ) + cos ( 4 x ) + 1 sin x · cos ( 3 x ) + cos x · sin ( 3 x )

В знаменателе у нас стоит формула синуса суммы. Тогда можно записать так:

y = sin ( 4 x ) + cos ( 4 x ) + 1 sin x · cos ( 3 x ) + cos x · sin ( 3 x ) = sin ( 4 x ) + cos ( 4 x ) + 1 sin ( 4 x ) = = 1 + cos ( 4 x ) sin ( 4 x )

У нас получилась сумма 3-х интегралов.

∫ sin ( 4 x ) + cos ( 4 x ) + 1 sin x · cos ( 3 x ) + cos x · sin ( 3 x ) d x = = ∫ d x + cos ( 4 x ) d x sin ( 4 x ) + ∫ d x sin ( 4 x ) = = x + 1 4 ln ∫ d ( sin ( 4 x ) ) sin ( 4 x ) + 1 4 ln cos ( 4 x ) - 1 sin ( 4 x ) = = 1 4 ln sin ( 4 x ) + 1 4 ln cos ( 4 x ) - 1 sin ( 4 x ) + C = x + 1 4 · ln cos 4 x - 1 + C

В некоторых случаях тригонометрические функции, находящиеся под интегралом, можно свести к дробно рациональным выражениям с использованием метода стандартной подстановки. Для начала возьмем формулы, которые выражают sin , cos и t g через тангенс половинного аргумента:

sin x = 2 t g x 2 1 + t g 2 x 2 , sin x = 1 - t g 2 x 2 1 + t g 2 x 2 , t g x = 2 t g x 2 1 - t g 2 x 2

Также нам нужно будет выразить дифференциал d x через тангенс половинного угла:

Поскольку d t g x 2 = t g x 2 ' d x = d x 2 cos 2 x 2 , то

d x = 2 cos 2 x 2 d t g x 2 = 2 d t g x 2 1 cos 2 x 2 = 2 d t g x 2 cos 2 x 2 + sin 2 x 2 cos 2 x 2 = 2 d t g x 2 1 + t g 2 x 2

Таким образом, sin x = 2 z 1 + z 2 , cos x 1 - z 2 1 + z 2 , t g x 2 z 1 - z 2 , d x = 2 d z 1 + z 2 при z = t g x 2 .

Найдите неопределенный интеграл ∫ d x 2 sin x + cos x + 2 .

Решение

Используем метод стандартной тригонометрической подстановки.

2 sin x + cos x + 2 = 2 2 z 1 + z 2 + 1 - z 2 1 + z 2 = z 2 + 4 z + 3 1 + z 2 ⇒ d x 2 sin x + cos x + 2 = 2 d z 1 + z 2 z 2 + 4 z + 3 1 + z 2 = 2 d z z 2 + 4 z + 3

Получим, что ∫ d x 2 sin x + cos x + 2 = 2 d z z 2 + 4 z + 3 .

Теперь мы можем разложить подынтегральную функцию на простейшие дроби и получить сумму двух интегралов:

∫ d x 2 sin x + cos x + 2 = 2 ∫ 2 d z z 2 + 4 z + 3 = 2 ∫ 1 2 1 z + 1 - 1 z + 3 d z = = ∫ d z z + 1 - ∫ C z + 3 = ln z + 1 - ln z + 3 + C = ln z + 1 z + 3 + C

Далее производим обратную замену z = t g x 2 :

∫ d x 2 sin x + cos x + 2 = ln z + 1 z + 3 + C = ln t g x 2 + 1 t g x 2 + 3 + C

Ответ: ∫ d x 2 sin x + cos x + 2 = ln t g x 2 + 1 t g x 2 + 3 + C

Важно отметить, что те формулы, которые выражают фукнции через тангенс половинного аргумента, не являются тождествами, следовательно, получившееся в итоге выражение ln t g x 2 + 1 t g x 2 + 3 + C – это множество первообразных функции y = 1 2 sin x + cos x + 2 только на области определения.

Для решения других типов задач можно использовать основные методы интегрирования.

Интегрирование функций рационально зависящих от тригонометрических функций

1. Интегралы вида ∫ sin n xdx , ∫ cos n xdx , n>0
a) Если n нечётное, то одну степень sinx (либо cosx ) следует внести под знак дифференциала, а от оставшейся чётной степени следует перейти к противоположной функции.
б) Если n чётное, то пользуемся формулами понижения степени
2sin 2 x=1-cos2x , 2cos 2 x=1+cos2x .
2. Интегралы вида ∫ tg n xdx , ∫ ctg n xdx , где n – целое.
Необходимо использовать формулы

3. Интегралы вида ∫ sin n x·cos m x dx
а) Пусть m и n разной чётности. Применяем подстановку t=sin x , если n - нечётное либо t=cos x , если m – нечётное.
б) Если m и n чётные, то пользуемся формулами понижения степени
2sin 2 x=1-cos2x , 2cos 2 x=1+cos2x .
4. Интегралы вида
Если числа m и n одинаковой чётности, то используем подстановку t=tg x . Часто бывает удобным применить приём тригонометрической единицы.
5. ∫ sin(nx)·cos(mx)dx , ∫ cos(mx)·cos(nx)dx , ∫ sin(mx)·sin(nx)dx

sin α·cos β = ½(sin(α+β)+sin(α-β))
cos α·cos β = ½(cos(α+β)+cos(α-β))
sin α·sin β = ½(cos(α-β)-cos(α+β))

С помощью данного онлайн-калькулятора можно вычислять интегралы по частям. Решение сохраняется в формате Word . Также рекомендуется ознакомиться с возможностью нахождения интегралов онлайн.

Примеры
1. Вычислить интеграл ∫ cos 4 x·sin 3 xdx .
Делаем замену cos(x)=t . Тогда ∫ cos 4 x·sin 3 xdx =
2. Вычислить интеграл .
Делая замену sin x=t , получаем

3. Найти интеграл .
Делаем замену tg(x)=t . Подставляя, получаем

Интегрирование выражений вида R(sinx, cosx)

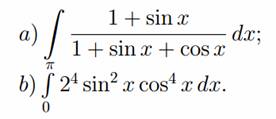
Пример №1 . Вычислить интегралы:

Решение.
а) Интегрирование выражений вида R(sinx, cosx) , где R — рациональная функция от sin x и cos x , преобразуются в интегралы от рациональных функций с помощью универсальной тригонометрической подстановки tg(x/2) = t .
Тогда имеем

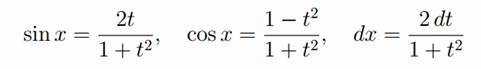
Если выполняется равенство R(-sin x, cos x) = -R(sin x, cos x)dx , то применяется подстановка cos x = t .
Если выполняется равенство R(sin x, -cos x) = -R(sin x, cos x)dx , то подстановка sin x = t .
Если выполняется равенство R(-sin x, -cos x) = R(sin x, cos x)dx , то подстановка tgx = t или ctg x = t .

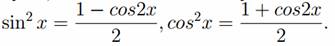
b) Во втором примере рассмотрим важный частный случай, когда общее выражение ∫ R(sinx, cosx) dx имеет вид ∫ sin m x·cos n xdx . В этом частном случае, если m нечетно, следует применить подстановку cos x = t . Если нечетно n , следует применить подстановку sin x = t . Если оба показателя тип — четные неотрицательные числа (в частности, одно из них может быть равным нулю), то выполняют замену по известным тригонометрическим формулам:
В данном случае

Представлены основные тригонометрические формулы и основные подстановки. Изложены методы интегрирования тригонометрических функций – интегрирование рациональных функций, произведение степенных функций от sin x и cos x, произведение многочлена, экспоненты и синуса или косинуса, интегрирование обратных тригонометрических функций. Затронуты нестандартные методы.

Основные тригонометрические формулы

Ниже приведены некоторые тригонометрические формулы, которые могут понадобится при интегрировании тригонометрических функций.

sin 2 a + cos 2 a = 1

sin ( a+b ) = sin a cos b + cos a sin b
cos ( a+b ) = cos a cos b – sin a sin b
sin 2 a = 2 sin a cos a
cos 2 a = cos 2 a – sin 2 a = 2 cos 2 a – 1 = 1 – 2 sin 2 a

Стандартные подстановки при интегрировании тригонометрических функций

Здесь мы рассмотрим стандартные подстановки, с помощью которых, в большинстве случаев, выполняется интегрирование тригонометрических функций.

Подстановка t = sin x

Преобразование выполняется по формулам:

cos x dx = dt ;
sin x = t ; cos 2 x = 1 – t 2 ;
;

Подстановка t = cos x

sin x dx = – dt ;
cos x = t ; sin 2 x = 1 – t 2 ;
;

Подстановка t = tg x

Подстановка t = ctg x

Подстановка t = tg (x/2)

Интегрирование обратных тригонометрических функций

Интегралы, содержащие обратные тригонометрические функции
arcsin φ , arctg φ , и т.д., где φ – некоторая алгебраическая функция от x , нередко интегрируются по частям, полагая u = arcsin φ , u = arctg φ , и т.д.

Стандартные методы интегрирования тригонометрических функций

Общий подход

Вначале, если это необходимо, подынтегральное выражение нужно преобразовать, чтобы тригонометрические функции зависели от одного аргумента, который совпадал бы с переменной интегрирования.

Например, если подынтегральное выражение зависит от sin( x+a ) и cos( x+b ) , то следует выполнить преобразование:
cos ( x+b ) = cos ( x+a – ( a–b ) ) = cos ( x+a ) cos ( b–a ) + sin ( x+a ) sin ( b–a ) .
После чего сделать замену z = x+a . В результате, тригонометрические функции будут зависеть только от переменной интегрирования z .

Когда тригонометрические функции зависят от одного аргумента, совпадающим с переменной интегрирования (допустим это z ), то есть подынтегральное выражение состоит только из функций типа sin z , cos z , tg z , ctg z , то нужно сделать подстановку
.
Такая подстановка приводит к интегрированию рациональных или иррациональных функций (если есть корни) и позволяет вычислить интеграл, если он интегрируется в элементарных функциях.

Однако, часто можно найти другие методы, которые позволяют вычислить интеграл более коротким способом, основываясь на специфике подынтегрального выражения. Ниже дано изложение основных таких методов.

Методы интегрирования рациональных функций от sin x и cos x

Рациональные функции от sin x и cos x – это функции, образованные из sin x , cos x и любых постоянных с помощью операций сложения, вычитания, умножения, деления и возведения в целочисленную степень. Они обозначаются так: R (sin x, cos x ) . Сюда также могут входить тангенсы и котангенсы, поскольку они образованы делением синуса на косинус и наоборот.
Интегралы от рациональных функций имеют вид:
.

Методы интегрировании рациональных тригонометрических функций следующие.
1) Подстановка всегда приводит к интегралу от рациональной дроби. Однако, в некоторых случаях, существуют подстановки (они представлены ниже), которые приводят к более коротким вычислениям.
2) Если R (sin x, cos x ) умножается на –1 при замене cos x → – cos x , то выполняется подстановка t = sin x .
3) Если R (sin x, cos x ) умножается на –1 при замене sin x → – sin x , то выполняется подстановка t = cos x .
4) Если R (sin x, cos x ) не меняется как при одновременной замене cos x → – cos x , и sin x → – sin x , то применяется подстановка t = tg x или t = ctg x .

Произведение степенных функций от cos x и sin x

Интегралы вида

являются интегралами от рациональных тригонометрических функций. Поэтому к ним можно применить методы, изложенные в предыдущем разделе. Ниже рассмотрены методы, основанные на специфике таких интегралов.

Если m и n – рациональные числа, то одной из подстановок t = sin x или t = cos x интеграл сводится к интегралу от дифференциального бинома.

Если m и n – целые числа, то интегрирование выполняется с помощью формул приведения:

Интегралы от произведения многочлена и синуса или косинуса

Интегралы вида:
, ,
где P(x) – многочлен от x , интегрируются по частям. При этом получаются следующие формулы:

Интегралы от произведения многочлена, экспоненты и синуса или косинуса

Интегралы вида:
, ,
где P(x) – многочлен от x , интегрируются с помощью формулы Эйлера
e iax = cos ax + i sin ax (где i 2 = – 1 ).
Для этого методом, изложенном в предыдущем пункте, вычисляют интеграл
.
Выделив из результата действительную и мнимую часть, получают исходные интегралы.

Нестандартные методы интегрирования тригонометрических функций

Ниже приведены ряд нестандартных методов, которые позволяют выполнить или упростить интегрирование тригонометрических функций.

Зависимость от (a sin x + b cos x)

Если подынтегральное выражение зависит только от a sin x + b cos x , то полезно применить формулу:
,
где .

Разложение дроби из синусов и косинусов на более простые дроби

Рассмотрим интеграл
.
Наиболее простой способ интегрирования заключается в разложении дроби на более простые, применяя преобразование:
sin( a – b ) = sin( x + a – ( x + b ) ) = sin( x+a ) cos( x+b ) – cos( x+a ) sin( x+b )

Интегрирование дробей первой степени

При вычислении интеграла
,
удобно выделить целую часть дроби и производную знаменателя
a ₁sin x + b ₁cos x = A ( a sin x + b cos x ) + B ( a sin x + b cos x )′ .
Постоянные A и B находятся из сравнения левой и правой частей.

На данном уроке мы рассмотрим интегралы от тригонометрических функций, то есть начинкой интегралов у нас будут синусы, косинусы, тангенсы и котангенсы в различных комбинациях. Все примеры будут разобраны подробно, доступно и понятно даже для чайника.

Для успешного изучения интегралов от тригонометрических функций Вы должны хорошо ориентироваться в простейших интегралах, а также владеть некоторыми приемами интегрирования. Ознакомиться с этими материалами можно на лекциях Неопределенный интеграл. Примеры решений и Метод замены переменной в неопределенном интеграле.

А сейчас нам потребуются: Таблица интегралов, Таблица производных и Справочник тригонометрических формул. Все методические пособия можно найти на странице Математические формулы и таблицы. Рекомендую всё распечатать. Особо заостряю внимание на тригонометрических формулах, они должны быть перед глазами – без этого эффективность работы заметно снизится.

При нахождении интегралов от тригонометрических функций используется ряд методов:

В рамках урока я постараюсь подробно разобрать все перечисленные методы и привести примеры решения типовых интегралов. Следует отметить, что данное разделение по параграфам весьма условно, поскольку очень часто вышеперечисленные правила используются одновременно.

Использование тригонометрических формул

Найти неопределенный интеграл.

Сначала полное решение, потом комментарии.

(1) Мы видим, что в подынтегральном выражении находится произведение двух функций. К сожалению, в интегральном исчислении нет удобной формулы для интегрирования произведения: , поэтому приходится прибегать к различным ухищрениям. В данном случае мы прерываем решение значком и поясняем, что используется тригонометрическая формула. Данная формула превращает произведение в сумму.

(2) Используем свойства линейности неопределенного интеграла – интеграл от суммы равен сумме интегралов; константу можно (и нужно) вынести за знак интеграла.

! Справка: При работе с тригонометрическими функциями следует помнить, что:

Косинус – это четная функция, то есть , минус исчезает без всяких последствий. В рассматриваемом примере:

Синус – функция нечетная: – здесь минус, наоборот – не пропадает, а выносится.

(3) Под интегралами у нас сложные функции (косинусы не просто от , а от сложного аргумента). Это простейшие из сложных функций, интегралы от них удобнее найти методом подведения под знак дифференциала. Более подробно с данным приёмом можно ознакомиться на уроке Метод замены переменной в неопределенном интеграле.

Найти неопределенный интеграл.

Это пример для самостоятельного решения, полное решение и ответ – в конце урока.

Найти неопределенный интеграл.

Классика жанра для тех, кто тонет на зачёте. Как Вы, наверное, заметили, в таблице интегралов нет интеграла от тангенса и котангенса, но, тем не менее, такие интегралы найти можно.

(1) Используем тригонометрическую формулу

(2) Подводим функцию под знак дифференциала.

(3) Используем табличный интеграл .

Найти неопределенный интеграл.

Это пример для самостоятельного решения, полное решение и ответ – в конце урока.

Найти неопределенный интеграл.

Степени у нас будут потихоньку повышаться =).
Сначала решение:

(1) Используем формулу

(2) Используем основное тригонометрическое тождество , из которого следует, что .

(3) Почленно делим числитель на знаменатель.

(4) Используем свойство линейности неопределенного интеграла.

(5) Интегрируем с помощью таблицы.

Найти неопределенный интеграл.

Это пример для самостоятельного решения, полное решение и ответ – в конце урока.

Также существуют интегралы от тангенсов и котангенсов, которые находятся в более высоких степенях. Интеграл от тангенса в кубе рассмотрен на уроке Как вычислить площадь плоской фигуры? Интегралы от тангенса (котангенса) в четвертой и пятой степенях можно раздобыть на странице Сложные интегралы.

Понижение степени подынтегральной функции

Данный приём работает, когда подынтегральные функции нафаршированы синусами и косинусами в чётных степенях. Для понижения степени используют тригонометрические формулы , и , причем последняя формула чаще используется в обратном направлении: .

Найти неопределенный интеграл.

В принципе, ничего нового здесь нет, за исключением того, что мы применили формулу (понизив степень подынтегральной функции). Обратите внимание, что я сократил решение. По мере накопления опыта интеграл от можно находить устно, это экономит время и вполне допустимо при чистовом оформлении заданий. В данном случае целесообразно не расписывать и правило , сначала устно берем интеграл от 1, затем – от .

Найти неопределенный интеграл.

Это пример для самостоятельного решения, полное решение и ответ – в конце урока.

Таки обещанное повышение степени:

Найти неопределенный интеграл.

Сначала решение, потом комментарии:

(1) Готовим подынтегральную функцию для применения формулы .

(2) Собственно применяем формулу.

(3) Возводим знаменатель в квадрат и выносим константу за знак интеграла. Можно было поступить несколько иначе, но, на мой взгляд, так удобнее.

(4) Используем формулу

(5) В третьем слагаемом снова понижаем степень, но уже с помощью формулы .

(6) Приводим подобные слагаемые (здесь я почленно разделил и выполнил сложение ).

(7) Собственно берём интеграл, правило линейности и метод подведения функции под знак дифференциала выполняем устно.

(8) Причесываем ответ.

! В неопределенном интеграле нередко ответ можно записать несколькими способами

В только что рассмотренном примере окончательный ответ можно было записать иначе – раскрыть скобки и даже это сделать еще до интегрирования выражения, то есть вполне допустима следующая концовка примера:

Вполне возможно, что такой вариант даже удобнее, просто я объяснил так, как сам привык решать). Вот еще один характерный пример для самостоятельного решения:

Найти неопределенный интеграл.

Это пример решается двумя способами, и у Вас могут получиться два совершенно разных ответа (точнее говоря, они будут выглядеть совершенно по-разному, а с математической точки зрения являться эквивалентными). Скорее всего, Вы не увидите наиболее рациональный способ и помучаетесь с раскрытием скобок, использованием других тригонометрических формул. Наиболее эффективное решение приведено в конце урока.

Подытоживая параграф, сделаем вывод: любой интеграл вида , где и – чётные числа, решается методом понижения степени подынтегральной функции.
На практике мне встречались интегралы с 8 и 10 степенями, решать их ~~ужасный гемор~~ приходилось, понижая степень несколько раз, в результате чего получались длинные-длинные ответы.

Метод замены переменной

Как уже упоминалось в статье Метод замены переменной в неопределенном интеграле, основной предпосылкой для использования метода замены является тот факт, что в подынтегральном выражении есть некоторая функция и её производная :
(функции , не обязательно находятся в произведении)

Найти неопределенный интеграл.

Смотрим в таблицу производных и замечаем формулы , , то есть, в нашем подынтегральном выражении есть функция и её производная. Однако мы видим, что при дифференцировании косинус и синус взаимно превращаются друг в друга, и возникает вопрос: как выполнить замену переменной и что же обозначать за – синус или косинус?! Вопрос можно решить методом научного тыка: если мы неправильно выполним замену, то ничего хорошего не получится.

Общий ориентир: в похожих случаях за нужно обозначить функцию, которая находится в знаменателе.

Прерываем решение и проводим замену

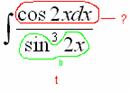
В знаменателе у нас всё хорошо, всё зависит только от , теперь осталось выяснить, во что превратится .
Для этого находим дифференциал :

Или, если короче:
Из полученного равенства по правилу пропорции выражаем нужное нам выражение:

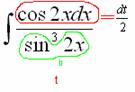
Итак:

Теперь всё подынтегральное выражение у нас зависит только от и можно продолжать решение

Готово. Напоминаю, что цель замены – упростить подынтегральное выражение, в данном случае всё свелось к интегрированию степенной функции по таблице.

Я не случайно так подробно расписал этот пример, это сделано в целях повторения и закрепления материалов урока Метод замены переменной в неопределенном интеграле.

А сейчас два примера для самостоятельного решения:

Найти неопределенный интеграл.

Полные решения и ответы в конце урока.

Найти неопределенный интеграл.

Здесь опять в подынтегральном выражении находятся синус с косинусом (функция с производной), но уже в произведении, и возникает дилемма – что же обозначать за , синус или косинус?

Можно попытаться провести замену методом научного тыка, и, если ничего не получится, то обозначить за другую функцию, но есть:

Поэтому проведем замену:

Если у кого остались трудности с алгоритмом замены переменной и нахождением дифференциала , то следует вернуться к уроку Метод замены переменной в неопределенном интеграле.

Найти неопределенный интеграл.

Кстати, эти ориентиры справедливы не только для тригонометрических функций.

А выражаем через синус с помощью основного тригонометрического тождества:

Вот теперь замена:

В рассмотренном примере в нечетной степени у нас находился косинус, поэтому мы отщипнули от степени один косинус, а за обозначили синус.

Найти неопределенный интеграл.

Степени идут на взлёт =).
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

Универсальная тригонометрическая подстановка

Найти неопределенный интеграл.

Универсальная тригонометрическая подстановка в данном случае реализуется следующим способом. Проведем замену: . Я использую не букву , а букву , это не является каким-то правилом, просто опять же я так привык решать.

Здесь удобнее находить дифференциал , для этого из равенства , я выражаю :
Навешиваю на обе части арктангенс:

Арктангенс и тангенс взаимно уничтожаются:

На практике можно не расписывать так подробно, а просто пользоваться готовым результатом:

При замене синусы и косинусы у нас превращаются в следующие дроби:
, , эти равенства основаны на известных тригонометрических формулах: ,

Итак, чистовое оформление может быть таким:

Проведем универсальную тригонометрическую подстановку:

(1) Производим в исходный интеграл подстановку: , , .

(2) Приводим знаменатель к общему знаменателю.

(3) Избавляемся от четырехэтажности дроби, при этом у нас сокращается. Раскрываем скобки в знаменателе, двойку в числителе выносим за знак интеграла.

(4) Приводим подобные слагаемые в знаменателе.

(5) Интеграл решается методом выделения полного квадрата. Более подробно с этим методом можно ознакомиться на уроке Интегрирование некоторых дробей. Разложение является подготовкой для осуществления вышеуказанного приёма

(6) Выделяем полный квадрат и готовим интеграл для интегрирования.

(7) Интегрируем по табличной формуле .

(8) Проводим обратную замену, вспоминая, что .

Рассмотрим похожий интеграл: , нет, решать мы его не будем =), а просто поймем как проводить замену.

Здесь тоже проводится универсальная тригонометрическая подстановка: .
Обратите внимание, что аргумент под тангенсом должен быть в два раза меньше, чем под синусом и косинусом. Формулы , сохраняют статус-кво, а вот дифференциал будет немного другой (я не зря недавно так подробно его расписал):

Интеграл решается путем замены и т.д., всё точно так же, единственное отличие, дифференциал будет опять немного другой.

Найти неопределенный интеграл.

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

С помощью универсальной тригонометрической подстановки решаются и интегралы вроде такого:

Найти неопределенный интеграл.

Здесь перед применением универсальной тригонометрической подстановки необходимо понизить степени в знаменателе при помощи формул , . Попробуйте разобраться в данном примере самостоятельно, полное решение и ответ очень близко!

Применение универсальной тригонометрической подстановки часто приводит к длинным и трудоемким вычислениям. Поэтому на практике универсальной тригонометрической подстановки стараются избегать (если возможно). Для этого используют ряд методов и приемов, о которых можно прочитать в статье Сложные интегралы.

Решения и ответы:

Пример 2: Решение:

Пример 4: Решение:

Пример 6: Решение:

Пример 8: Решение:

Пример 10: Решение:

Пример 12: Решение:

Примечание: здесь можно было сделать замену , но гораздо выгоднее обозначить за весь знаменатель.

Пример 13: Решение:

Пример 16: Решение:

Пример 18: Решение:

Проведем универсальную тригонометрическую подстановку:

Пример 19: Решение:

Универсальная тригонометрическая подстановка:

Вы выполнили проверку? Может я и ошибся где ;)

Автор: Емелин Александр

(Переход на главную страницу)

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

Рассмотрим несколько видов интегралов от тригонометрических функций.

R(sin x, cos x)− рациональная функция от sin x и cos x . Это означает, что над аргументами производятся только рациональные операции: сложение, вычитание, умножение, деление, возведение в целые степени (положительные и отрицательные). Интегралы этого вида приводятся к рациональной функции от x универсальной тригонометрической подстановкой:

Следует заметить, что, применяя эту подстановку можно привести любую подынтегральную функцию R(sin x, cos x) − к рациональной дроби, но иногда получаются громоздкие дроби, которые трудно проинтегрировать.

Рассмотрим частные случаи, когда можно избежать универсальной подстановки.

Где m и n – целые положительные числа. Если m и n – четные, то используется тригонометрические формулы понижения степени,

III. Если одно из чисел m или n – нечетное, или m и n – нечетные, то отделяем от нечетной степени один множитель и делаем замену cos x = t (или sin x = t) – sin xdx = dt