Тела вращения в повседневной жизни доклад
Обновлено: 22.04.2024
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
по математике "Тела вращения и их использование в жизни"
1. Авторы проекта – учащиеся группы № 14 Головков Алексей и Дудольский Владимир, руководитель проекта – преподаватель математики Грибова О.М.
2. Предмет – математика, 2 курс СПО.
3. Сроки реализации 01.10.2017 – 01.05.2018 г.
4. Краткая аннотация проекта.
Проект является личностно ориентированным, так как предполагает возможность участия в нем различного уровня подготовки учащихся. В ходе реализации проекта учащиеся не только знакомятся с основным материалом учебной темы, но и получают дополнительные знания по моделированию многогранников и тел вращения, учатся находить и использовать на практике межпредметные связи, знания различных наук.
- формирование группы учащихся;
- составление плана работы;
- формулирование вопросов для исследований;
- подбор информационных ресурсов для проекта;
- введение в проблематику проекта с помощью вводной лекции преподавателя;
- выявление предварительных знаний учеников по теме проекта, выяснение тем исследований, интересных учащимся;
- формулирование проблемных и частных вопросов проекта, темы исследования;
- планирование исследований (цели, задачи, гипотеза, методы);
- обсуждение с учениками возможных источников информации;
- определение этапов работы над проектом.
Исследовательский . Исследования, проводимые в рамках проекта:
Этапы работы над проектом .
Самостоятельная работа учащихся: проведение исследований, сбор информации, самостоятельный поиск информации в Интернете. Сохранение результатов в формате Word.
Работа с учебником, печатными материалами. Изучение методических материалов, предлагаемых к проекту. Составление плана презентации. Оформление результатов исследований с помощью презентации.
Презентация результатов, защита проекта.
В Древней Греции геометрия считалась одним из семи свободных искусств по уровню обучения. Остальными являлись Грамматика, Риторика, Диалектика, Арифметика, Музыка и Астрономия. Д ревние египтяне относились с большим почтением к геометрии, так как по её законам двигаются все тела на нашей планете, в нашей вселенной. Геометрические тела разных форм, разных размеров встречаются в нашем мире повсеместно, поэтому очень важно знать их свойства. Поэтому мы выбрали эту тему. Мы считаем, что именно эта тема актуальна в наше время. В нашем проекте мы постараемся дать подробную характеристику телам вращения, так как они широко распространены в окружающем нас пространстве: животном и растительном мире, архитектуре и жизни людей.
Цели проекта:
- вовлечение каждого ученика в активный познавательный процесс;
- расширение и углубление знаний по изучаемой теме;
- воспитание коммуникативных навыков, навыков сотрудничества;
- формирование умений в построении фигур вращения.
- формирование навыков исследовательской работы;
- развитие творческих способностей;
- развитие интереса к предмету, умений обобщать и систематизировать материал;
- применять теоретические знания при построении фигур вращения,
Содержание работы
Параболоид вращения
Архимед (лат. Archimedes, греч. Архимидис) (около 287 до н.э., Сиракузы, Сицилия - 212 до н.э.) - древнегреческий ученый, математик и механик, основоположник теоретической механики и гидростатики. Он впервые упоминает о параболоиде в своем трактате "О коноидах и сфероидах".
Параболо́ид ― тип поверхности второго порядка. Параболоид может быть охарактеризован как незамкнутая нецентральная (то есть не имеющая центра симметрии) поверхность второго порядка.
Эллиптический параболоид называется параболоидом вращения . Если вращать параболу y = ах² вокруг своей оси то получится поверхность, которую называют параболоидом вращения .
параболоид Параболоид вращения
Лучи идущие параллельно оси параболоида после отражения от граней параболоида концентрируются в одной точке называемой фокусом параболоида. На этом свойстве устроены параболические телескопы, параболические антенны, прожектора, проекторы, автомобильные фары.
Если же источник света поместить в фокус параболоида, то лучи, идущие от источника света, будут концентрироваться в световой пучок, идущий параллельно оси параболоида. Этот факт находит применение при создании прожекторов, фонарей, проекторов, где зеркало имеет форму параболоида.
Поверхность жидкости в равномерно вращающемся сосуде является параболоидом вращения.
Если плоскость сечения цилиндра составляет некоторый угол с плоскостью основания и не пересекает основания, то в сечении будет фигура, ограниченная эллипсом.

Фокальное свойство эллипса. Внутри эллипса существуют такие точки F1 и F2, называемые фокусами эллипса, что сумма расстояний от любой точки А эллипса до этих точек есть величина постоянная.
Окружность является частным случаем эллипса. Наряду с гиперболой и параболой, эллипс является коническим сечением. Эллипс - ортогональная проекция окружности на плоскость.
проходящий через фокусы эллипса отрезок AB, концы которого лежат на эллипсе, называется большой осью данного эллипса;
отрезок CD, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса;
точка пересечения большой и малой осей эллипса называется его центром .
Эллипсоид вращения (сфероид)
нормальный
Эллипсо́ид враще́ния - это фигура вращения в трёхмерном пространстве, образованная при вращении эллипса вокруг одной из его главных осей.
вытянутый сплюснутый
Цилиндр – это геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Цилиндр образуется при вращении прямоугольника вокруг прямой, содержащей его сторону.
Основные элементы цилиндра:
прямой круговой цилиндр - это тело, получаемое вращением прямоугольника вокруг одной из его сторон;
сторона прямоугольника, вокруг которой производилось вращение, называется осью цилиндра;
радиус основания является радиусом цилиндра;
расстояние между основаниями цилиндра называется его высотой;
любой отрезок, параллельный оси цилиндра и соединяющий граничные точки его оснований, называется образующей цилиндра.
Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих. Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований.
Наклонный цилиндр – цилиндр, образующие которого не перпендикулярны плоскостям его оснований. Объём цилиндра равен произведению площади основания на высоту. (рис. 3)

основания цилиндра равны, так как параллельный перенос есть движение;
основания цилиндра лежат в параллельных плоскостях, так как при параллельном переносе плоскость переходит в параллельную плоскость;
образующие цилиндра параллельны и равны, так как при параллельном переносе точки смещаются по параллельным прямым на одно и то же расстояние.
секущая плоскость проходит вдоль оси цилиндра. Такое сечение называется осевым;
секущая плоскость перпендикулярна оси цилиндра. Сечением является круг;
секущая плоскость параллельна оси цилиндра. Сечением является прямоугольник;
секущая плоскость наклонена к плоскости основания. Сечением является эллипс.
Призмой , вписанной в цилиндр , называется такая призма, у которой плоскостями оснований являются плоскости оснований цилиндра, а боковыми ребрами – образующие цилиндра.
Призмой, описанной около цилиндра , называется призма, у которой плоскостями оснований являются плоскости оснований цилиндра, а боковые грани касаются цилиндра.
Касательной плоскостью к цилиндру называется плоскость, проходящая через образующую цилиндра и перпендикулярная плоскости осевого сечения, содержащей эту образующую.
Конус – тело, ограниченное конической поверхностью и кругом с границей L.
Рассмотрим окружность L с центром О и прямую ОР перпендикулярную к плоскости ß этой окружности. Через точку Р и каждую точку окружности проведём прямую. Поверхность, образованная этими прямыми, называется конической поверхностью , а прямые – образующими конической поверхности . Точка Р называется вершиной , прямая ОР – осью конической поверхности. Круг называется основанием конуса. Вершина конической поверхности – вершиной конуса. Отрезки образующих, заключённых между вершиной и основанием, называются боковой поверхностью конуса. Ось конической поверхности называется осью конуса, а её отрезок, заключённый между вершиной и основанием, - высотой конуса. Конус может быть получен вращением прямоугольного треугольника вокруг одного из своих катетов.
Например, данный конус был получен вращением прямоугольного треугольника ABC вокруг катета АВ.
Осевое сечение . Если сечение конуса проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого - диаметр основания конуса, а боковые стороны - образующие конуса.
Если секущая плоскость перпендикулярна к оси конуса, то сечение конуса представляет собой круг с центром, расположенным на оси конуса.
Радиус r΄ этого круга равен РО΄/РО • r , где r – радиус основания конуса
За площадь боковой поверхности конуса принимается площадь её развёртки, которая равна произведению половины длины окружности основания на образующую S=πrl.
Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. Для вычисления S полной поверхности конуса получается формула S=πr(l+r).
Усечённый конус
Возьмём произвольный конус и проведём секущую плоскость, перпендикулярно к его оси. Эта плоскость пересекается с конусом по кругу и разбивает конус на две части. Одна из частей представляет собой конус, а другая называется усечённым конусом . Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усечённого конуса, а отрезок, соединяющий их центры, - высотой усечённого конуса.
Часть конической поверхности, ограничивающая усечённый конус, называется его боковой поверхностью , а отрезки образующих конической поверхности, заключённые между основаниями, называются образующими усечённого конуса. Все образующие равны друг другу.
Усечённый конус может быть получен вращением прямоугольный трапеции вокруг её боковой стороны, перпендикулярной к основаниям. Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую, т.е. S=π(r+r΄)l, где r и r΄-радиусы оснований, l - образующая усечённого конуса.
Шар — геометрическое тело ; совокупность всех точек пространства, находящихся от центра на расстоянии , не больше заданного. Это расстояние называется радиусом шара . Шар образуется вращением полукруга около его неподвижного диаметра . Этот диаметр называется осью шара , а оба конца указанного диаметра — полюсами шара . Поверхность шара называется сферой : замкнутый шар включает эту сферу , открытый шар — исключает.

Если секущая плоскость проходит через центр шара, то сечение шара называется большим кругом . Другие плоские сечения шара называются малыми кругами .
Практическое применение фигур вращения
Конусообразные формы встречаются в конструкциях крон и стволов деревьев, стеблей и соцветий, грибов, раковин и пр. В природе встречаются конусообразные формы двух типов. Первый тип предназначен для обеспечения устойчивости. Ему соответствует статичный конус, или конус гравитации(конус основанием вниз). Это оптимальная форма для сопротивления ветровым нагрузкам и действию силы тяжести. Ее легко увидеть в форме кроны или ствола ели, шляпки или ножки белого гриба.
Второй тип соответствует началу развития и выражается в форме динамического конуса или конуса роста (конус основанием вверх). Примерами конуса роста является гриб лисичка, лишайник кладония красноплодная.
В природе обычно встречаются не чистые типы конусов, а сочетание двух типов. Комбинации разных по типу конусов дают начало различным формообразованиям, например, кроны многих деревьев.
в архитектуре - купол Исаакиевского собора, Адмиралтейский шпиль, купола церквей и соборов и многое другое.
в повседневной жизни – посуда, бытовые приборы, отдельные элементы конструкции зданий, предметы обихода, изделия гончарного производства.
в научной деятельности - лабораторное оборудование, элементы зданий, детали приборов
Над проектом работали
Руководитель : Грибова Ольга Михайловна.
Значение изучения свойств тел вращения трудно переоценить. Важную роль играет знакомство с ними в связи с подготовкой учащихся к практической жизни, к труду. Форму тел вращения имеют многие детали машин, приборов. При обработке металла или дерева на токарном станке в промышленности очень быстро и с высокой степенью точности изготавливают детали, имеющие форму цилиндра, конуса или шара. Телами вращения являются и изделия гончарного производства.
Теоретический материал раздела о телах вращения по объему бывает невелик. Изучение данной темы методом проекта потребовало от авторов пректа больше времени на самостоятельную работу, работу за компьютером. В ходе реализации проекта учащиеся не только познакомились с основным материалом учебной темы, но и получили дополнительные знания по моделированию тел вращения, научились находить и использовать на практике межпредметные связи, знания различных наук. Конечным продуктом проекта является презентация проекта.

Тема: Тела вращения в быту Проект выполнила : Студентка 14 -НК Линькова А.А.

Актуальность темы: расширяет знания в области геометрии позволяет узнать о геометрических фигурах, которые встречаются в быту архитекторы создают проекты с использованием форм тел вращения.


Задачи: Узнать историю появление тел вращения Распространение тел вращения в быту Использование тел вращения в архитектуре

Тела вращения — объёмные тела, возникающие при вращении плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости. Тела вращения — объёмные тела, возникающие при вращении плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости.

История создания: Первоначальные сведений о свойствах геометрических фигур люди нашли, наблюдая за окружающим миром и в практической деятельности. Позже ученые заметили, что некоторые свойства тел можно выводить путем рассуждения. Так возникли теоремы и доказательства.

В связи с развитием мореплавании были нужны астрономические наблюдения, что заставляло человека изучать свойства шара.

Уже в 7 в. до нашей эры в Греции начали накапливаться знания в области стереометрии.

Начали формироваться представления о пространственных фигурах и доказательства их свойств. Важную роль в исследовании стереометрии внес греческий математик Евклид. Начали формироваться представления о пространственных фигурах и доказательства их свойств. Важную роль в исследовании стереометрии внес греческий математик Евклид.


Шар — геометрическое тело; совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного. Шар образуется вращением полукруга около его неподвижного диаметра. Этот диаметр называется осью шара, а оба конца указанного диаметра — полюсами шара. Поверхность шара называется сферой: замкнутый шар включает эту сферу, открытый шар — исключает. Шар — геометрическое тело; совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного. Шар образуется вращением полукруга около его неподвижного диаметра. Этот диаметр называется осью шара, а оба конца указанного диаметра — полюсами шара. Поверхность шара называется сферой: замкнутый шар включает эту сферу, открытый шар — исключает.

Свойства шара Шар является открытым множеством в топологии, порождённой метрикой. Замкнутый шар — замкнутым множеством в топологии, порождённой метрикой. По определению такой топологии открытые шары с центрами в любой точке являют собой её базу.

Формула вычисления объема шара: Площадь поверхности шара:

Геометрическая фигура шар встречается в быту. Например, футбольный мяч, елочная игрушка, глобус, надувной круг. Геометрическая фигура шар встречается в быту. Например, футбольный мяч, елочная игрушка, глобус, надувной круг.


Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.

Свойства цилиндра: Если плоскость основания цилиндра параллельна плоскости направляющей, то граница этого основания будет по форме совпадать с направляющей кривой.



Геометрическая фигура цилиндр встречается в быту. Например, свеча, кастрюля, чашка


Конус — тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность. Конус — тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность. Свойства конуса: Все образующие конуса равны. Углы наклона образующих к основанию равны. Углы между осью и образующими равны. Углы между осью и основанием прямые.

Свойства конуса: Все образующие конуса равны. Углы наклона образующих к основанию равны. Углы между осью и образующими равны. Углы между осью и основанием прямые.

Площадь боковой поверхности конуса вычисляется по формуле: Площадь боковой поверхности конуса вычисляется по формуле: S(бок.)=πRl, где R — радиус конуса, l — образующая конуса. Площадь основания конуса вычисляется по формуле S(полн.) = S(бок.) + S(круга) = S(круга) =πR2. Площадь полной поверхности конуса вычисляется по формуле S(полн.) =S(бок.) +S(круга) =πRl+πR2. Объём конуса вычисляют по формуле V = 13⋅H⋅ S(круга) = πR2⋅H3


Геометрическая фигура конус встречается и в быту. Например, мороженное, детская пирамида, елка.

Вывод Знание геометрических фигур не только расширяет кругозор человека , но и применяются в разных областях человеческой деятельности. Во многих профессиях они просто необходимы. Например, профессия архитектор, который занимается организацией пространства, разрабатывает сложнейшие чертежи зданий с необычной формой. Конструктор , который занимается технологическим проектированием , разрабатывает конструкции различного назначения и форм. И этот список можно перечислять долго . Из выше сказанного , можно сделать вывод, что знание геометрических фигур очень важно для человека .

Проект по геометрии: "Тела вращения. Использование тел вращения как элементов в архитектуре города Волгограда и других крупных городов мира" для 11 класса.
Проект по геометрии:
Тема: Тела вращения.
Использование тел вращения как элементов в архитектуре города Волгограда и других крупных городов мира.
МАОУ Светлоярской СШ № 2 им. Ф. Ф. Плужникова
Киселева Татьяна Владимировна

Основные этапы исследовательской работы:
Актуальность выбранной темы:
- Я считаю, что данная тема проекта актуальна, потому что она, в первую очередь, расширяет интересы в области геометрии. Затем позволяет нам узнать о том, что геометрические фигуры встречаются и окружают нас в нашей повседневной жизни. Также многие архитекторы создают проекты будущих сооружений с использованием форм тел вращения.
Цель исследовательской работы:
Изучить понятие тела вращения.
Изучить какие тела вращения существуют.
Исследовать архитектуру крупных городов мира и найти в ней элементы тел вращения.

Задачи исследовательской работы:
Тела вращения – это…
Какие существуют тела вращения?
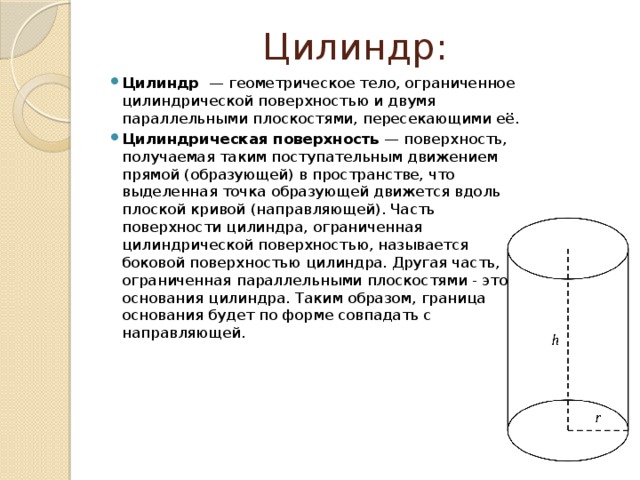
- Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
- Цилиндрическая поверхность — поверхность, получаемая таким поступательным движением прямой (образующей) в пространстве, что выделенная точка образующей движется вдоль плоской кривой (направляющей). Часть поверхности цилиндра, ограниченная цилиндрической поверхностью, называется боковой поверхностью цилиндра. Другая часть, ограниченная параллельными плоскостями - это основания цилиндра. Таким образом, граница основания будет по форме совпадать с направляющей.
Архитектурные сооружения города Волгограда

Зал Воинской Славы.



Казанский кафедральный собор.

Строительство стадиона. (Чемпионат мира по футболу 2018 год)

Сфера в виде земного шара. (Городская скульптура)

Другие архитектурные сооружения…

Дом Мельникова (Дом-мастерская архитектора Константина Степановича Мельникова)

Штаб-квартира BMW

Gate Tower Building


Шуховская башня (Шуховская телебашня, Шаболовская телевизионная башня, Радиобашня Шухова)



Математика (геометрия) для творческого труда архитектора издавна признается чем-то очень важным, необходимым и плодотворным. И все же архитектурная наука так до сих пор и не разработала должным образом этот, можно сказать, кардинальный вопрос теории. Речь идет не только о ремесленном или техническом вооружении зодчего, о реализации идеи в проекте и сооружении, но и о творческом процессе поиска, о "формах" самой идеи, о "формах" художественного мышления.
На языке архитектуры, можно сказать, что геометрия – это грандиозное мысленное сооружение, которое в свернутом, понятийном, символьном виде моделирует окружающий нас мир и происходящие в нем явления. Я пронаблюдала, как геометрия помогает добиться прочности, удобства, красоты архитектурных сооружений.

Я считаю, что я справилась с поставленными задачами и целями, которые были поставлены в начале моего проекта.
А) Я изучила всю ту информацию, которая мне была необходима, интересна.
Б) Мне было интересно узнать, что лежит в основе архитектурных сооружений, некоторые из которых я посещала в настоящей жизни.
Вы можете изучить и скачать доклад-презентацию на тему Тела вращения. Презентация на заданную тему содержит 19 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас - поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!


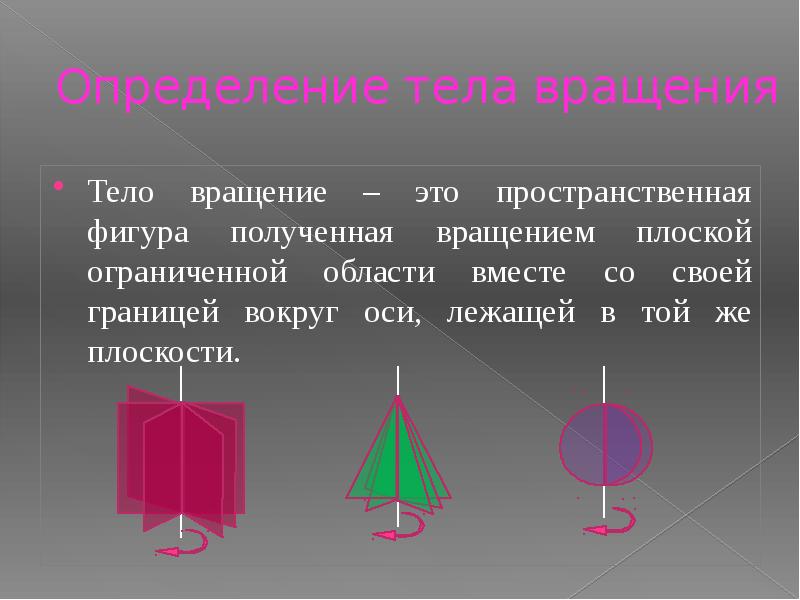















Определение тела вращения Тело вращение – это пространственная фигура полученная вращением плоской ограниченной области вместе со своей границей вокруг оси, лежащей в той же плоскости.
Цилиндр Цилиндр – это тело, которое описывает прямоугольник при вращении около оси, содержащей его сторону. Верхний и нижний круги – это основания цилиндра. Прямая проходящая через центры кругов – это ось цилиндра. Отрезок параллельный оси цилиндра, концы которого лежат на окружностях основания – это образующая цилиндра. Радиус основания - это Высота цилиндра - это перпендикуляр между основаниями цилиндра
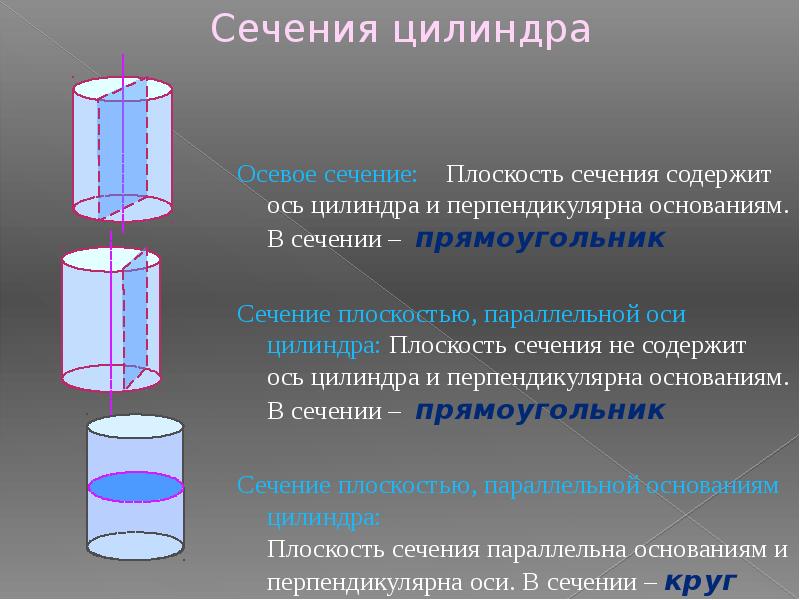
Сечения цилиндра Осевое сечение: Плоскость сечения содержит ось цилиндра и перпендикулярна основаниям. В сечении – прямоугольник Сечение плоскостью, параллельной оси цилиндра: Плоскость сечения не содержит ось цилиндра и перпендикулярна основаниям. В сечении – прямоугольник Сечение плоскостью, параллельной основаниям цилиндра: Плоскость сечения параллельна основаниям и перпендикулярна оси. В сечении – круг
Площадь поверхности цилиндра Для вывода формулы площади полной поверхности цилиндра потребуется развертка цилиндра. Полная поверхность состоит из 2 оснований и боковой поверхности. Площадь основания находим как площадь круга: S = R2 R – радиус основания цилиндра. Боковая поверхность цилиндра есть прямоугольник. Одна сторона прямоугольника -это высота цилиндра(h), другая – длина окружности основания (2R) Площадь боковой поверхности цилиндра равна произведению сторон прямоугольника: 2Rh
Конус Конус (круговой конус) – тело, которое состоит из круга – основание конуса, точки, не принадлежащей плоскости этого круга, – вершины конуса и всех отрезков, соединяющих вершину конуса и точки окружности основания. Отрезки, которые соединяют вершину конуса с точками окружности основания, называются образующими конуса. Поверхность конуса состоит из основания и боковой поверхности.
Конус Конус – это тело, которое описывает прямоугольный треугольник при вращении вокруг оси, содержащей его катет. Точка вне круга с которой соединяются все точки окружности – это вершина конуса. Прямая проходящая через центр круга и вершину конуса – есть ось конуса. Отрезок соединяющий вершину с любой точкой окружности основания – это образующая конуса. Радиус основания - это радиус конуса. Высота конуса - это перпендикуляр, опущенный из вершины конуса к основанию.
Сечение конуса Сечение плоскостью, параллельной основанию конуса: Плоскость сечения параллельна основанию конуса и перпендикулярна оси. В сечении – круг.
Площадь поверхности конуса Для вывода формулы площади полной поверхности конуса потребуется его развертка. Полная поверхность состоит из основания и боковой поверхности. Площадь основания находим как площадь круга S = R2 R – радиус основания цилиндра Боковая поверхность конуса есть. Площадь боковой поверхности конуса равна произведению радиуса на образующую и число . Получаем, Sполн = Sбок + Sосн = Rl + R2
Шар Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от заданной точки точки. Эта точка называется центром шара Расстояние от центра шара до любой точки поверхности называется – радиусом шара Шар можно получить вращением полукруга вокруг оси, содержащей его диаметр. Сфера – это поверхность все точки которой равноудалены от заданной точки.
Сечения шара Сечение шара, проходящее через его центр: В сечении –круг. В этом случае в сечении получается круг наибольшего радиуса, его называют большой круг шара. Сечение плоскостью, не проходящей через центр шара: В сечении – круг. Площадь поверхности шара равна четыре площади большого круга шара: S = 4R2
Задача на цилиндр Решение. 1) Если дно шляпы опустить на плоскость её полей, то получим круг радиуса R = r1+ 10 = 20 cм. 2) Площадь этого круга 3) Найдем площадь боковой поверхности цилиндрической части 4) Найдем площадь шляпы
Задача на конус Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Задач на шар Найдите длину полярного круга Земли (радиус Земли принять за 6400 км) 1)Из справочника: длина дуги от экватора до полярного круга 66. Этой же мере соответствует центральный угол АОВ = 66 2)Дуга от Северного полюса до экватора равна 90. Значит, СОВ = 90. Тогда, СОА = 90 - 66 = 24. 3)Используя синус угла СОА в прямоугольном АСО найдем СА: CA= AO· sin(COA)= 6400 · sin 24 = 6400 · 0,4067= 2602,88 (км) 4) СА есть радиус окружности полярного круга, найдем длину этой окружности: 2·CA =2· 3,14· 2602,88 = 16 346, 0864 км Ответ: длина полярного круга ≈ 16 тыс. км
Читайте также:

