Соизмеримые и несоизмеримые отрезки доклад

Обновлено: 05.07.2024

1 1 Соизмеримые величины Научно-исследовательская работа. Выполнили ученики 6 класса Подбельская Ольга. Капаржан Вера. Научный руководитель Учитель математики высшей категории Пряженникова Н.В.

3 3 Оглавление Введение. 1. Глава 1. Соизмеримые величины. 1.1 Соизмеримые и несоизмеримые величины 1.2 Теория о соизмеримых отрезках 1.3 Рациональные и иррациональные числа 2. Глава 2. Решение задач способом соизмеримости величин 3. Глава 3. Парадоксы. 4. Заключение

4 4 Соизмеримые и несоизмеримые величины. Это две однородные величины(например длины или площади), обладающие или не обладающие общей мерой. Если величины соизмеримы, то их отношение выражается рациональным числом. Если несоизмеримы, то их отношение выражается иррациональным числом(например площадь круга и площадь квадрата)

5 5 Теория о соизмеримых отрезках Пусть даны два отрезка а и в. Они называются соизмеримыми, если существует такой отрезок с, который укладывается несколько раз в отрезках а и в( разное количество раз)

6 6 Рациональные и иррациональные числа. Рациональное число можно представить в виде дроби,где числитель-целое число знаменатель-натуральное. Рациональное число представляется конечной десятичной дробью (например 24,5). Иррациональное число представляется бесконечной непериодической дробью (например π3,14…).

7 7 Задачи Найти способ измерения: 1. Высоты здания, не поднимаясь на него. 2. Высоты дерева,не забираясь на него.

8 8 Идея решения 1. С помощью длинной веревки измерить высоту не получится, поскольку нельзя подниматься на здание. 2. С помощью вертолета или пожарной машины? Но у нас нет такой техники. 3.Летом, в солнечный день по длине тени, отбрасываемой деревом или зданием по способу Фалеса Милетского. Но лета еще нет.

9 9 Реализуем задуманное Перебрав варианты,мы решили, что : 1. Соизмеримые величины высота человека высота здания или дерева. 2. Выбрали мерку Оля Вера

10 10 Оборудование 1.Фотоаппарат. 2.Компьютер. 3.Флеш-носитель. 4. Измерительный метр. 5.Линейка.

11 11 Способ решения задачи 1 1. Вера встала вплотную к зданию. 2. Мы с фотоаппаратом выбрали удобное место (подальше от здания) 3. Сделали несколько снимков.Вера около здания. 4. Измерили рост Веры- 163 см 5. Измерили высоту здания на фотографии- 20 см 6. Измерили высоту Веры (мерки)на фотографии- 4 см 7. Разделили 20 :4=5 мерок Получили :высота здания равна 5 меркам. 8. Умножили 163x5 Получили 815 см Вывод: высота школы приближенно равна 8 м 15 см

12 12 Способ решения задачи 2 1. Оля встала вплотную к дереву. 2. Мы с фотоаппаратом выбрали удобное место и встали подальше. 3. Сделали несколько снимков: Оля – возле дерева 4. Измерили рост Оли-155 см 5. Измерили высоту дерева на фотографии- 21 см 6. Измерили высоту Оли(мерки) на фотографии-3 см 7. Разделили 21:3 Получили 7 Высота дерева равна 7 меркам 8. Умножили 7x155 Получили 1085 см Вывод: Высота сосны приближенно равна 11 метров

13 13 Парадокс Длины обладали общей мерой –высота ученика Отношение длин выражали дробью. Но получали приближенные значения дробей. О каких величинах мы говорим? Соизмеримых или несоизмеримых?

14 14 И гений-парадоксов друг Другие способы измерения высоты : 1. Способ Жюль Верна 2. При помощи записной книжки 3. При помощи зеркала 4. Высотомером 5. Через свойства подобных треугольников

15 15 Что дальше? При изучении ГЕОМЕТРИИ в 7-9 классах будем использовать МЕТОДЫ, основанные на других ТЕОРИЯХ.

ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА II

§ 40 Соизмеримые и несоизмеримые отрезки

Отрезок Δ называется общей мерой отрезков Δ₁ и Δ₂, если он укладывается целое число раз в каждом из этих отрезков.

Например, отрезок, EF, изображенный на рисунке 54, укладывается в АВ два раза, а в CD — 3 раза. Поэтому он является общей мерой отрезков АВ и CD. Аналогично этому, отрезок Δ₂, изображённый на рисунке 55, является общей мерой отрезкой Δ₁ и Δ₂, поскольку в Δ₁ он укладывается 4 раза, а в Δ₂ (в самом себе) — один раз.

Любые ли два отрезка имеют общую меру? Ответ на этот вопрос будет дан несколькими строками ниже. А пока мы введем еще одно определение.

Два отрезка, имеющие общую меру, называются соизмеримыми, а не имеющие общей меры — несоизмеримыми.

Теперь вопрос о том, любые ли два отрезка имеют общую меру, можно перефразировать таким образом: любые ли два отрезка являются соизмеримыми? Следующая теорема дает отрицательный ответ на этот вопрос.

Теорема. Диагональ любого квадрата несоизмерима с его стороной.

Доказательство будем проводить методом от противного. Предположим, что диагональ АС квадрата ABCD (рис. 56) соизмерима с его стороной АВ.

Тогда существует общая мера этих отрезков, то есть отрезок, который в АВ укладывается ровно п раз, а в АС ровно т раз. Если принять этот отрезок за единицу длины, то длина АВ выразится числом п, а длина АС — числом т.

На диагонали АС построим новый квадрат ACEF, как показано на рисунке 56. Очевидно, что площадь этого квадрата вдвое больше площади квадрата ABСD:

S_ABСD = n 2 , a S_ACEF= m 2 .

m 2 = 2n 2

( m /_n) 2 = 2

Следовательно, наше исходное предположение неверно. Остается признать, что диагональ любого квадрата несоизмерима с его стороной.

Теперь мы можем сделать два важных вывода.

1. Если отрезок CD соизмерим с единицей длины АB, то его длина выражается рациональным числом.

Действительно, в силу того что отрезки АВ и CD соизмеримы, найдется третий отрезок EF, который в АВ укладывается ровно п раз,, а в CD ровно т раз. Но в таком случае п-я часть отрезка АВ должна укладываться в CD ровно т раз. Поэтому длина CD выражается рациональным числом m /_n.

2. Если отрезок CD несоизмерим с единицей длины АВ, то длина его не выражается никаким рациональным числом.

Действительно, если бы длина отрезка CD выражалась некоторым рациональным числом, например p /_q, то q-я доля отрезка АВ укладывалась бы в АВ q раз, а в CD р раз. Нo в таком случае q-ю долю отрезка АВ можно было бы считать общей мерой отрезков АВ и CD. А это противоречит условию: отрезки АВ и CD несоизмеримы.

Упражнения

308. Докажите, что если отрезки АВ и CD соизмеримы, то п-я доля отрезка АВ соизмерима с т-й долей отрезка CD (m и п — произвольные натуральные числа).

309. Докажите, что если отрезки АВ и CD несоизмеримы, то п-я доля отрезка АВ несоизмерима с т-й долей отрезка CD (m и п — произвольные натуральные числа).

310. Пусть Δ₁ и Δ₂ — два соизмеримых отрезка, причем отрезок Δ₁ длиннее отрезка Δ₂. Докажите, что в таком случае отрезки Δ₁ + Δ₂ и Δ₁ — Δ₂ будут также соизмеримыми.

Верно ли обратное утверждение?

311. Докажите, что в прямоугольном треугольнике катет, лежащий против угла в 60°, несоизмерим с гипотенузой.

312. Докажите, что если отрезок АВ соизмерим с отрезком CD, а отрезок CD соизмерим с отрезком EF, то отрезок АВ соизмерим с отрезком EF.

313. Докажите, что если отрезок АВ соизмерим с отрезком CD, но несоизмерим с отрезком EF, то отрезки CD и EF несоизмеримы.

Пусть некоторый отрезок содержится в отрезке ровно и в отрезке ровно раза: , . Отрезок в таком случае называют общей мерой отрезков и . Ясно, что если взять любую долю отрезка , то она также будет содержаться в каждом из данных отрезков и целое число раз. Например, если , то , ; если , то , и т. д.

Общей мерой двух отрезков будет называться такой третий отрезок, который содержится целое число раз в каждом из двух данных отрезков.

Если отрезки имеют общую меру, то они имеют бесконечное множество общих мер. Одна из них больше всех остальных и называется наибольшей общей мерой данных отрезков. Если меньший из двух данных отрезков содержится в большем целое число раз, то меньший отрезок и является наибольшей общей мерой двух данных отрезков.

Два отрезка ( и ) называются соизмеримыми, если они имеют общую меру ( ): и , где и — натуральные числа.

Соизмеримые отрезки существуют, например, м и дм . Для нахождения их наибольшей общей меры отложим на ( раза) и получим в остатке отрезок ( дм ), меньший отрезка . Остаток отложится на меньшем отрезке ровно раза, т. е. и в большем отрезке раз, т. е. , поэтому и есть наибольшая общая мера отрезков и . Если бы, откладывая остаток на меньшем данном отрезке , опять получили бы остаток ( ), то откладывали бы на и т.д., пока не получилось бы, что отложится в целое число раз без остатка. Тогда и будет наибольшей общей мерой отрезков и .

Два отрезка называются несоизмеримыми, если они не имеют общей меры.

Примером несоизмеримых отрезков могут служить сторона и диагональ квадрата (доказательство этого факта опускаем) . Это значит, что процесс откладывания стороны квадрата на диагонали, остатка на стороне, второго остатка на первом и т. д. был бы бесконечен, так как всегда получался бы остаток. Измерить отрезок единичным отрезком значит найти число, показывающее, сколько раз отложится на отрезке отрезок или его доли. Это число называют длиной отрезка.
Если отрезок соизмерим с единичным отрезком , то длина отрезка есть число рациональное (натуральное или рациональная дробь). Например, дм при дм или м при м .
Если отрезок несоизмерим с единичным отрезком , то длина отрезка есть число иррациональное. Например, если дм сделать стороной квадрата, то его диагональ дм (по теореме Пифагора ). Поскольку иррациональное число есть бесконечная непериодическая десятичная дробь, то его приближенное значение можно выразить с любой степенью точности с помощью конечной (рациональной) дроби. Так, точная длина есть дм , а приближенная дм или дм и т. д.

Отношением двух отрезков называется отношение их длин, выраженных в одинаковых единицах измерения.

Величина отношения отрезков не изменится, если в качестве единицы измерения взять любую общую меру данных отрезков. Так, если и , то
и .

Четыре отрезка , , , называются пропорциональными, если из их длин можно составить пропорцию .

Этому определению не противоречит следующее более общее определение.
Отрезки называются пропорциональными отрезкам , если
.

Открытие несоизмеримости, т. е. обнаружение таких величин, отношение которых не может быть выражено с помощью отношения целых чисел, является наивысшим достижением пифагорейской школы и поворотным этапом в развитии всей математики. По силе революционизирующего воздействия это открытие, сделанное на рубеже VI — V вв. до н. э., можно сравнить разве что с открытием дифференциального и интегрального исчислений Ньютоном и Лейбницем в XVII в., открытием неевклидовой геометрии Лобачевским в XIX в. или теории относительности Эйнштейном в начале XX в.

Мы не знаем доподлинно, решение какой конкретной задачи привело пифагорейцев к открытию несоизмеримости. Это могло быть сделано в любом из пифагорейских учений: и в арифметике при нахождении средней геометрической чисел 1 и 2, и в геометрии при отыскании общей меры диагонали и стороны квадрата, и в музыке при попытках разделить октаву пополам, что также приводит к нахождению средней геометрической между числами 1 и 2.

Как бы то ни было, но бесспорным является то, что доказательство существования несоизмеримых величин было найдено ранними пифагорейцами и к середине V в. до н. э. было широко известно. Вот это доказательство.

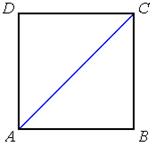
Теорема. Сторона AB и диагональ AC квадрата несоизмеримы, т. е. отношение не выражается отношением целых чисел (рис. 40).

Доказательство. Допустим противное. Пусть AC и AB соизмеримы, т. е. их отношение равно отношению целых чисел:

причем числа m и n одновременно не являются четными, так как иначе дробь можно было бы сократить на 2. Возводя (1.5.1) в квадрат, имеем

По теореме Пифагора , т. е. , и, значит,

т. е. четно. Согласно учению о четном и нечетном (см. с. 121) m также четно (так как произведение двух четных чисел четно, а двух нечетных—нечетно), т. е. , откуда . Тогда

т. е. четно, и, следовательно (учение о четном и нечетном), n также четно. Итак, m и n одновременно являются четными, что противоречит первоначальному допущению о несократимости дроби. Это противоречие доказывает теорему.

В качестве иллюстрации этой пифагорейской мысли рассмотрим метод Архита — нахождение приближенных значений иррациональных чисел. Метод Архита — античного знатока пропорций — основан на музыкальной пропорции (1.4.9).

Пусть даны два числа . Рассмотрим их среднее арифметическое и среднее гармоническое . Как мы показали (см. с. 140), и . Затем образуем те же средние из полученных значении: и и т. д. В результате получим две последовательности:

обладающие следующим свойством:

Обозначая , и переходя в равенствах (1.5.2) к пределу при , имеем

откуда легко находим, что . Учитывая это равенство и переходя к пределу в (1.5.3), получим

Итак, обе последовательности и при стремятся к числу .

Пусть теперь . Эти числа можно рассматривать как нулевые приближения числа , которое будет пределом последовательностей и . Найдем первые члены этих последовательностей:

Как видим, последовательности и очень быстро сходятся к своему пределу и уже их третьи члены дают прекрасное приближение (пять верных знаков!) числа ( — с избытком и — с недостатком). Попутно мы убеждаемся в справедливости пифагорейской мысли о том, что, чем больше целые числа в отношении, тем точнее они выражают иррациональное число.

Достаточно быстро было обнаружено, что диагональ и сторона квадрата не составляют исключения. К концу V в. до н. э. пифагореец Феодор из Кирены (? — 369 до н. э.), математик, астроном и музыковед, учитель Платона, показал, что стороны квадратов, площади которых равны 3, 5, 6, . , 15, несоизмеримы со стороной единичного квадрата, т. е. числа иррациональные.

Мы не знаем доказательства Феодора, но ясно, что он рассматривал каждую иррациональность в отдельности. Существуют различные гипотезы относительно того, почему Феодор не смог доказать иррациональность следующего числа: и выше. Наиболее убедительная из них утверждает, что все доказательства Феодора основывались только на учении о четном и нечетном, а первое число, для которого этот способ не проходит, как раз и есть .

Открытие несоизмеримости оказало решающее влияние на все дальнейшее развитие греческой математики. Поскольку некоторые геометрические объекты не измерялись отношением целых чисел, то естественно было предположить, что геометрические объекты являются величинами более общей природы, чем рациональные числа. Поэтому уже в пифагорейской школе предпринимается попытка построить всю математику, основываясь не на арифметике, а на геометрии. Для этого величины (и в первую очередь числа) представлялись отрезками, площадями и все алгебраические операции (в том числе и извлечение корня) интерпретировались геометрически. Более того, геометрически записывались и решались даже уравнения.

Читайте также: