Методы решения геометрических задач доклад

Обновлено: 05.07.2024

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке "Файлы работы" в формате PDF

2. Основная часть

4. Список используемой литературы

I Введение

Сегодня можно наблюдать стремительное изменение в окружающем нас мире. Эти изменения требуют от человека новых качеств. Прежде всего обществу нужны люди, способные нестандартно мыслить, принимать самостоятельные решения, даже самые абсурдные, быть инициативны. Все это можно развивать, решая задачи на уроках математики и во внеурочное время.

Отсюда вытекает гипотеза: если действоватьне по алгоритму, то можно найти другие способы решения геометрических задач.

Цель: найти разные способы решения геометрических задач.

Задачи: сделать анализ учебников по математике;

сгруппировать задачи геометрического характера;

решить задачи разными способами, рассуждая традиционно и

Объект: стандартные геометрические задачи с заданными величинами.

Предмет: найти способы решения геометрических задач.

Методы – практические и теоретические.

Значимость работы заключается в том, что, исследуя решения, мы найдем возможные способы. Вследствие этого будут развиваться различные типы и

виды мышления (синтез, анализ) и, затем на уроках, можно применять эти

способы к решению других геометрических задач, показать другим, что такие задачи можно решать разными способами.

II Основная часть

Все геометрические задачи можно разделить на четыре группы:

-нахождение площади (S);

-нахождение периметра (P);

-нахождение периметра прямоугольника, где неизвестна одна сторона;

- нахождение стороны прямоугольника по известному периметру;

Итак, теперь можно каждую группу проанализировать, выполняя решение.

III Описание исследовательской деятельности

Разделив задачи на группы, я начал решать, опираясь сначала на ранее изученные способы решения задач.

- Задачи на нахождение площади.

Длина прямоугольника 7 см, ширина на 3 см короче. Найти площадь.

1 способ. По формуле нахождения площади, мы знаем, что площадь прямоугольника - это произведение длины (а) на ширину (в).

По условию задачи нам известна ширина. Нам лишь сказано, что она короче длины на 3 см. Значит, нам нужно найти ширину, а поэтому из данных величин мы получим: 7 - 3 = 4 см.- ширина прямоугольника. Отсюда следует, что площадь можно найти так: S = 7 * 4 = 28 см 2 .

2 способ: Это решение нахождения площади выражением:

S = (7 – 3)* 7 = 28 см 2 .

Достроим прямоугольник до квадрата со стороной известной нам и равной 7 см, значит, площадь квадрата равна:

Найдем неизвестную ширину, ведь нам известно, что она короче длины на 3 см, а значит: 7- 3 = 4 см.- данная ширина.

Но мы достроим прямоугольник, данный нам до квадрата со стороной 7 см. Значит ширина достроенной фигуры сейчас составляет 4 см и 3 см. Площадь достроенной фигуры нами части равна: 3 * 7 = 21 см 2 .

Наша искомая площадь тогда составит:

S = 49 – 21 = 28 см 2 .- что нам и следовало найти.

Из данного условия задачи, нам нужно найти ширину прямоугольника, это

значит: 7 – 3 = 4 см.- ширина.

Зная, что ширина 4 см, мы можем уменьшить наш прямоугольник до квадрата со стороной 4 см и найти его площадь.

S = 4 * 4 = 16 см 2 .

А нам дано, что длина по условию задачи равна 7 см. Если сторона нашего квадрата 4см, значит можно найти длину второго прямоугольника:

При условии нам можно найти его площадь, ведь мы знаем, что его ширина 4см, а длина 3 см, значит S = 4 * 3 =12 см 2 .

А, теперь сложив площадь квадрата и площадь прямоугольника, мы можем смело найти площадь искомой нами фигуры – прямоугольника со сторонами 4см и 7 см

S = 16 см 2 +12 см 2 = 28 см 2

У данного вида задач я сумел найти четыре способа решения.

Задачи на нахождение периметра (Р).

Дан квадрат со стороной 5 см. Найти периметр этого квадрата.

1 способ: Нам известно, что периметр- это сумма длин всех сторон. Из этого следует, что Р=5 + 5 + 5 + 5 = 20 см.

2 способ: Периметр – сумма длин всех сторон, а значит, можно записать и так: сложив две стороны вместе и умножив на 2, т.к все стороны равны 5 см.

Р = (5 + 5) *2 = 20 см.

3 способ: Мы знаем, что у квадрата все стороны равны, их всего четыре. И нам известно, что сторона квадрата равна 5 см. Это значит, что

4 способ:А можно использовать и такой способ: ширину умножаем на 2 ( т.к две ширины в нашем квадрате) и длину тоже умножаем на 2, т.к квадрат это четырехугольник , у которого4 стороны, таким образом

Р = 5 * 2 + 5 * 2 = 20 см

5 способ: У квадрата все стороны одинаковые и равны 5 см. Мы можем

использовать и такой метод нахождения периметра: умножив сторону квадрата на три его стороны и прибавив еще одну сторону. Это будет выглядеть так: Р = (5 * 3) + 5 = 20 см.

Вот таким образом мы можем находить периметр квадрата, выбирая любой из пяти способов, которые я нашел.

Задачи на нахождение периметра прямоугольника, где одна из сторон неизвестна.

Допустим, нам дано условие: ширина прямоугольника 8 см, длина на 2 см больше. Найти периметр этого прямоугольника.

1 способ: По условию задачи нам известно ширина 8 см, а длина больше на 2 см. Из этого нам понятно, что нужно найти длину. Если сказано, что она на 2 см больше, это значит: 8 +2 = 10 см.- длина прямоугольника. По известной формуле нахождения периметра прямоугольника Р = (а + в)*2

Мы можем найти периметр, т.к знаем ширину и длину данного нам прямоугольника Р = (8 + 10 )* 2 = 36 см.

2 способ: Нам дан прямоугольник, у которого 4 стороны и одна из них равна 8 см, другая на 2 см больше. Значит: 8 + 2 = 10 см- длина прямоугольника.

Сейчас нам известно, что ширина равна 8 см, длина 10 см. В прямоугольнике 4 стороны, две из них равны 8 см, две другие 10 см. Значит,

Р = 8 + 8 + 10 + 10 = 36 см.

3 способ: Мы можем смело заменить 2 способ решения нашей задачи умножив ширину на число 2( т.к. две ширины у прямоугольника) и длину на 2 (т.к две стороны у прямоугольника).

Р = 8 *2 + 10 * 2 = 36 см.

4 способ: А можно найти периметр этого прямоугольника и другим способом:

Р = ( 8 + 10 ) + ( 8 + 10 ) = 36 см, т.е.прибавив ширину и длину прямоугольника дважды. Так можно находить периметр прямоугольника с одной неизвестной стороной.

Задачи на нахождение стороны прямоугольника по известному периметру.

Допустим, нам известен периметр. Он равен 24 см, найти длину, если ширина равна 5 см.

1 способ: Если периметр равен 24 см, ширина 5см, найдем длину. Мы знаем, что периметр равен сумме длин всех сторон, а это значит:

В эту формулу подставляем известные величины:

24 : 2 – 5 = 7 см- длина прямоугольника

2 способ: Эту задачу можно решить уравнением. Мы знаем ширину и значение периметра. Зная формулу нахождения периметра Р = ( а + в ) * 2. Значение длины заменим х, тогда получим:

х = 7 см - искомая длина прямоугольника.

3 способ: Зная, что ширина прямоугольника равна 5 см, мы можем умножить это значение на 2, потому что у прямоугольника 2 стороны одинаковые.

5 * 2 = 10 см – сумма длин 2 сторон.

А зная, что периметр равен 24 см 2 , можно найти сумму длин двух других сторон. 24-10=14см

А теперь 14 см поделим на 2 (т.к 2другие стороны одинаковы) Длина прямоугольника равна 7см.

4 способ:Зная периметр прямоугольника и одну его ширину, мы можем выяснить, сколько сантиметров приходится на 3 другие стороны. Зная формулу нахождения периметра – сумма длин всех сторон, мы можем составить выражение:

24 – 5 = 19 см – приходится на три остальные стороны. Но в прямоугольнике 2 равные длины. Это значит из оставшейся суммы нам надо вычесть еще 5 см и получим:

19 – 5 = 14 см – приходится на 2 другие стороны. И они между собой тоже равны. Получим: 14 : 2 = 7 см – длина прямоугольника.

IV Заключение

Проделав практическое исследование, я нашел кроме известных способов решения геометрических задач, с которыми нас знакомят на уроках математики, 4 , а иногда и 5 способов решения. Значит, геометрические задачи можно решать разными способами, подходя к ним творчески и нестандартно. Конечно, для этого нужно время, но если заниматься этим постоянно и систематически, то поиск способов будет проходить быстрее.

Наше предположение по решению геометрических задач разными способами доказано. Решением геометрических задач можно заниматься и в свободное от уроков время и в любой обстановке. Способы решения можно применять к другим задачам данного вида. Это полезная работа. Она приводит к развитию личностных качеств, развитию мышления, помогает углублению знаний в курсе математики и творчески подходить к решению задач.

Список используемой литературы

1. Беденко М.В. Сборник текстовых задач по математике для 1-4 кл.- М.: ВАКО, 2006 г.- 272 с.- (Мастерская учителя).

2. Изучение трудных тем по математике в 1-3 классах: Из опыта работы учителей г. Москвы (Составила Н.Г.Уткина)- М.Просвещение, 1982-159с.

6. Лавлинскова Е.Ю. Методика работы с задачами повышенной трудности в начальной школе.- Волгоград: Панорама, 2006-112 с.

При решении геометрических задач обычно используются три основных метода: геометрический – когда требуемое утверждение выводится с помощью логических рассуждений из ряда известных теорем; алгебраический – когда искомая геометрическая величина вычисляется на основании различных зависимостей между элементами геометрических фигур непосредственно или с помощью уравнений; комбинированный – когда на одних этапах решение ведется геометрическим методом, а на других - алгебраическим.

Какой бы путь решения ни был выбран, успешность его использования зависит, естественно, от знания теорем и умения их применять.

Метод дополнительного построения

Метод подобия

Подобие треугольников

Две фигуры F и F ₁ называются подобными, если они переводятся друг в друга преобразованием подобия, т.е. таким преобразованием, при котором расстояния между точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз.

Признаки подобия треугольников:

1) Если два угла одного соответственно равны двум углам другого;

2) Если две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами равны;

3) Если три стороны одного треугольника пропорциональны трем сторонам другого.

Метод замены

Метод введения вспомогательного неизвестного

Суть метода заключается в том, что исходя из условия задачи составляют уравнение (или систему уравнений). В качестве вспомогательных аргументов удобно выбирать величины, которые вместе с данными из условия задачи дают набор элементов, однозначно задающих некоторую фигуру.

Метод площадей

В математических задачах часто бывает полезен такой прием: двумя способами найти одну и ту же величину и приравнять полученные для нее выражения. Пусть мы, например, двумя способами нашли площадь некоторой фигуры. Если в одном из выражений для площади входит, скажем синус какого-либо угла α, то при помощи соотношения из полученного равенства можно получить некоторое неравенство, порой интересное.

Векторный метод

Применение критериев коллинеарности и компланарности векторов в решении задач.

Критерии коллинеарности и компланарности векторов служат основной для применения векторной алгебры в решении стереометрических задач. Они позволяют выразить в виде векторных равенств различные утверждения о расположенных точках, прямых и плоскостей в пространстве. Переход от векторных равенств к скалярным происходит на основе единственности разложения вектора по двум неколлинеарным и трём некомпланарным векторам.

Координатный метод

Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. И, решая ту или иную геометрическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще, удобнее. Некоторые виды координатных систем, отличные от прямоугольных.

1.Косоугольные (аффинные) координаты.

Рассмотрим самые употребительные и простые координаты в пространстве, называемые прямоугольными. Их называют ещё декартовыми по имени Рене Декарта (1596-1650) – французского учёного и философа, впервые ввёдшего координаты в геометрию (на плоскость).

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Технология решения геометрических задач.

Процесс решения задачи можно разбить на 11 этапов. Приведу памятку, содержащую последовательность выполнения данных этапов работы. Однако, при решении ни каждой задачи следует выполнять все перечисленные этапы(например, может не понадобиться чертёж или деталировка, не всегда удаётся сразу выстроить алгоритм решения задачи и т.д.)

Чтение условия задачи

Выполнение чертежа с буквенными обозначениями

Краткая запись условия задачи (формирование базы данных)

Перенос данных условия на чертёж; при необходимости можно выделить элементы чертежа разным цветом

Запись требуемых формул и теорем на черновике

Анализ данных задачи, привязка искомых величин к элементам чертежа

Реализация алгоритма решения

Проверка правильности решения

Чтение условия задачи

Прочитать условие задачи. В условиях задач могут упоминаться различные понятия, которые необходимо вспомнить. Выпишите на черновике нужное определение, формулировку теоремы или формулы. Все эти знания являются исходными для решения задачи и поэтому важны.

Выполнение чертежа с буквенными обозначениями

Чертёж – это рабочее место, пространство, которое необходимо организовать так, чтобы работать было удобно. Хороший чертёж – это залог правильно решённой задачи. Поэтому не надо мельчить и экономить бумагу, ведь хороший чертёж поможет увидеть связи между элементами изучаемых фигур, после чего останется оформить решение. Механизм построения чертежа надо обосновывать. Для решения задачи вам могу понадобиться дополнительные построения, которые выполняются либо одновременно с основными, либо в процессе решения.

Краткая запись условия задачи

Краткая запись условия задачи выполняется с использованием введённых на чертеже буквенных обозначений. На основе краткой записи осуществляется математическая запись решения задачи. В краткой записи отделите исходные данные, от того что надо доказать, построить или найти. Краткая запись условия задачи – это база данных для её решения.

Перенос данных условия на чертёж

Запись требуемых формул и теорем на черновике

Читая условие задачи, необходимо выписать на черновике всю информацию, которая связана с каждым из терминов, используемых в условии задачи. Затем, если понятно, как сгруппировать информацию, надо расположить её в нужном порядке. Эта информация является базой знаний. Чем полнее и точнее будет база знаний, тем больше шансов, что в неё попадут именно те формулы, определения и свойства, которые необходимо использовать. Поэтому если сразу решить задачу не удаётся, то анализируйте и осмысливайте весь относящийся к ней теоретический материал. В процессе работы может быть найден план решения.

Этот этап работы необязателен. Его приходится выполнять в тех случаях, когда чертёж к задаче громоздкий и не обладает достаточной наглядностью для последующего анализа. Деталировка полезна тогда, когда не ясно, какая фигура получилась в результате геометрических построений, какие прямые параллельны, перпендикулярны и т.д. Суть деталировки заключается в том, что фигуры на дополнительных чертежах можно разворачивать удобным для их изучения образом. Исходная сложная задача в результате деталировки разбивается на несколько более простых.

Анализ данных задачи, привязка искомых величин к элементам чертежа

На этом этапе выясняем, существует ли фигура, которая содержит искомую величину. Допустим, существует. Тогда выясняем, какие элементы этой фигуры надо знать, чтобы найти искомую величину. Есть ли они в данных задачи? Если нет, то из каких данных задачи их можно найти?

В сложных задачах по ходу решения могут использоваться и несколько фигур и деталировок, для каждой фигуры анализируется теоретический материал и данные условия задачи, затем составляется цепочка, алгоритм решения.

Реализация алгоритма решения

На этом этапе, в зависимости от стоящей перед нами задачи, осуществляются требуемые доказательства, построения или вычисления. Последовательность действий соответствует при этом пунктам выстроенной цепочки.

Проверка правильности решения

Характер проверки зависит от типа решаемой задачи.

В задачах на доказательство полезно заново проследить логику проведённых рассуждений и убедиться в том, что они не содержат противоречий.

В задачах на построение основным объектом проверки является обоснованность выполненных действий.

При проверке задач на вычисление надо убедиться, что найденные величины имеют геометрический смысл.

При проверке решения задач всех типов необходимо также убедиться, что использованы все данные условия.

Запись ответа

2. Халатное построение чертежа (от руки, без чертежных инструментов).

3. Неправильный перенос данных задачи на чертеж (либо по незнанию,

либо по небрежности).

4. Неумение проанализировать условие задачи и выявить неизвестные величины,

возможность нахождения которых вытекает прямо из условия задачи.

5. Неумение применять формулы и теоремы к решению задач.

6. Несоблюдение этапов решения задачи.

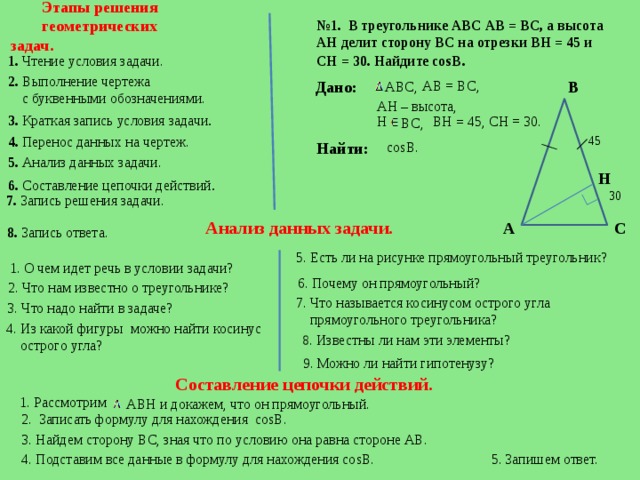
Этапы решения

геометрических задач.

№ 1. В треугольнике АВС АВ = ВС, а высота АН делит сторону ВС на отрезки ВН = 45 и

СН = 30. Найдите cosB .

1. Чтение условия задачи.

2. Выполнение чертежа

с буквенными обозначениями.

3. Краткая запись условия задачи .

ВН = 45, СН = 30.

4. Перенос данных на чертеж.

5. Анализ данных задачи.

6. Составление цепочки действий .

7. Запись решения задачи.

Анализ данных задачи.

8. Запись ответа.

5. Есть ли на рисунке прямоугольный треугольник?

1. О чем идет речь в условии задачи?

6. Почему он прямоугольный?

2. Что нам известно о треугольнике?

7. Что называется косинусом острого угла

3. Что надо найти в задаче?

4. Из какой фигуры можно найти косинус

8. Известны ли нам эти элементы?

9. Можно ли найти гипотенузу?

Составление цепочки действий.

АВН и докажем, что он прямоугольный.

2. Записать формулу для нахождения cosB.

3. Найдем сторону ВС, зная что по условию она равна стороне АВ.

4. Подставим все данные в формулу для нахождения cosB.

5. Запишем ответ.

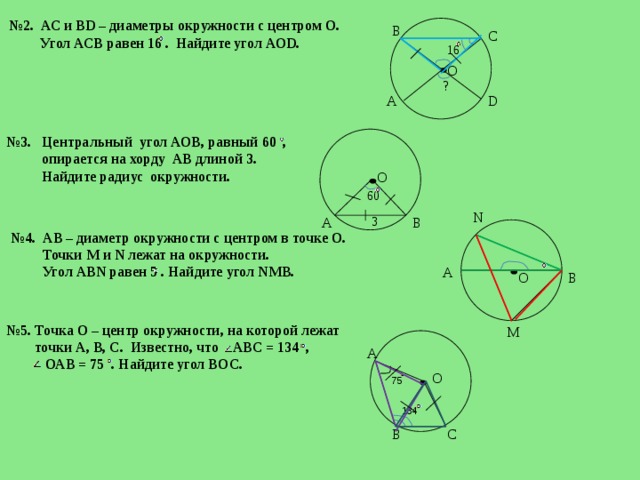
№ 2. АС и ВD – диаметры окружности с центром О.

Угол АСВ равен 16 . Найдите угол АОD.

№ 3. Центральный угол АОВ, равный 60 ,

опирается на хорду АВ длиной 3.

Найдите радиус окружности.

№ 4. АВ – диаметр окружности с центром в точке О.

Точки М и N лежат на окружности.

Угол АВN равен 5 . Найдите угол NМВ.

№ 5. Точка О – центр окружности, на которой лежат

точки А, В, С. Известно, что АВС = 134 ,

ОАВ = 75 . Найдите угол ВОС.

№ 6. В параллелограмме ABCD проведены перпендикуляры

ВЕ и DF к диагонали АС. Докажите, что отрезки BF и DE равны.

Джорж Бернард Шоу

Умение мыслить математически – одна из благороднейших способностей человека.

-75%

Читайте также: