Математические модели переходных процессов доклад

Обновлено: 04.07.2024

При классификации переходных процессов, различают волновые процессы, электромагнитные и электромеханические. Здесь рассмотрены два последних вида переходных процессов.
Из общих уравнений Парка — Горева, изложенных ниже, могут быть найдены значения токов при любых переходных процессах в системах, в том числе при коротких замыканиях, однако в этом разделе не приводятся расчетные выражения для определения этих токов.
Расчеты по уравнениям Парка — Горева (П.-Г.) довольно сложны и проводятся только при применении вычислительных машин. Обычно при аналитических расчетах, расчетах с помощью статических моделей (расчетных столов) и значительной части расчетов, выполняемых на вычислительных машинах, целесообразно пользоваться упрощенными уравнениями. Правильный выбор системы уравнений и необходимой точности анализа, соответствующей реальной технической задаче, составляет искусство инженера.
Дифференциальные уравнения синхронных машин дают возможность проводить анализ переходных процессов в электрических системах с учетом наибольшего количества влияющих факторов (изменений угловой скорости ротора, апериодических составляющих токов статора, периодических токов ротора, активного сопротивления в цепи статора генератора). Опустив те или иные члены в уравнениях П. — Г., можно получить упрощенные уравнения, применяющиеся: а) для расчетов токов коротких замыканий (без учета изменений скорости); б) для расчета электромеханических переходных процессов, обычно без учета апериодических составляющих тока, статора и периодических тока ротора.
Уравнения П. — Г. связывают мгновенные значения токов, магнитных потоков, напряжений в осях координат (d, q), жестко связанных с ротором.

Мгновенные значения параметров режима — фазные и в осях d, q
Эти значения определяют как проекции на оси времени фаз а, b , с вектора тока, вращающегося со скоростью w . Этот вектор тока (напряжения, э. д. с, потокосцепления) называют обобщенным.
Оси времени фаз, а, b , с неподвижны и совпадают с осями обмоток статора (рис. 37-1):

где a — произвольный угол.
Проекции обобщенного вектора тока на оси d и q, жестко связанные с ротором, дают значения, продольного и поперечного токов (рис. 37-2):

При наличии токов нулевой последовательности в системе имеет место соотношение

Соотношения, аналогичные приведенным выше, справедливы для напряжений, э. д. с. и потокосцеплений.
Соотношения между мгновенными значениями фазных величин и величинами в продольной и поперечной осях имеют вид:

Угол g меняется во времени:

где — полное потокосцепление статора в продольной оси; — то же в поперечной оси; — ток нулевой последовательности.
В случае симметричного режима системы токи нулевой последовательности отсутствуют и выражения упрощаются.
Значения и определяются из выражений:

где G(p)-операторная проводимость машины; X_d ( p)-операторное сопротивление машины в продольной оси; X_q (p)-то же в поперечной оси; U_B — напряжения возбуждения машины.
Для машины без успокоительных обмоток и эквивалентных им контуров

Если известна э. д. с. E_q, по можно найти так:

Для машины с успокоительными обмотками в продольной и поперечной осях и определяются теми же уравнениями.

Рис. 37-2. Положение обобщенного вектора тока I в пространстве и его проекции на продольную и поперечную оси ротора.

Уравнения Парка — Горева для синхронной машины в операторной форме
Эти уравнения при принятых на рис. 37-3 направлениях осей имеют вид:

В системе относительных единиц ; тогда .

Третье уравнение системы относится к случаю несимметричного режима или несимметричной схемы.
Уравнения, приведенные выше, полностью описывают переходный процесс машины, работающей на шины неизменного напряжения. Для анализа переходного процесса в сложной системе уравнения составляются для каждого элемента (генераторов, нагрузок, участков сети) и решаются совместно.

Решение уравнений, описывающих переходный процесс в системе
Решение приведенной выше системы уравнений относительно токов или других величин, рассматриваемых как неизвестные, проводится в операторной форме (для изображений). Например, находятся значения токов в виде:

где D₁(p), D₂(p)-частные определители системы; D(p)-общий определитель системы.
Характер переходного процесса в системе определяется знаком вещественной части корней определителя D(p). При переходный процесс затухающий.
Если изменения напряжений заданы, то можно записать:

Токи как функции времени находят, переходя от изображения к оригиналам, что может быть сделано с помощью формулы разложения.

Уравнения для вращающего момента и мощности во время относительного движения ротора
При принятых направлениях осей (рис. 37-3) момент электромагнитных сил, действующих на ротор, в общем случае имеет вид

При подстановке и выраженных через токи и реактивные сопротивления, электромагнитный момент может быть вычислен согласно

В системе относительных единиц, где коэффициент 3/2 учтен соответствующим выбором базисных величин,

Связь между мощностью, отдаваемой в сеть, и моментом следующая:

где в относительных единицах;

Электромагнитная мощность генератора, передаваемая с ротора на статор,

Уравнение относительного движения ротора в общем виде:

В относительных единицах

Упрощенные уравнения Парка — Горева для определения параметров режима при переходных электромеханических процессах
Эти уравнения применяются при расчетах токов коротких замыканий, устойчивости и т. д. При этом отказываются от учета влияния:
1) апериодической составляющей тока статора (трансформаторной э. д. с);
2) периодических токов ротора, связанных с апериодическими составляющими тока статора;
3) активного сопротивления в цепи статора.
Тогда в системе относительных единиц при уравнения П.- Г. для синхронной машины будут иметь вид:

В соответствии с этим упрощаются выражения для токов:
Выражения мощности и электромагнитного момента в этих условиях будут совпадать, так как при принятых предпосылках отдаваемая мощность численно равна вращающему моменту. Для симметричного или условно приведенного к симметричному режима (метод симметричных составляющих) получим:

Здесь и берутся с учетом принятых допущений.
Уравнение относительного движения ротора при принятых допущениях имеет вид

На основе упрощенного выражения момента можно перейти к ряду частных его выражений.

Актуальность проблемы. . Математические методы позволяют упорядочить систему экономической информации, выявлять недостатки в имеющейся информации и вырабатывать требования для подготовки новой информации или ее корректировки. Разработка и применение экономико-математических моделей указывают пути совершенствования экономической информации, ориентированной на решение определенной системы задач планирования и управления. Прогресс в информационном обеспечении планирования и управления опирается на бурно развивающиеся технические и программные средства информатики. Интенсификация и повышение точности экономических расчетов. Формализация экономических задач и применение ЭВМ многократно ускоряют типовые, массовые расчеты, повышают точность и сокращают трудоемкость, позволяют проводить многовариантные экономические обоснования сложных мероприятий, недоступные при господстве"ручной" технологии. Углубление количественного анализа экономических проблем. Благодаря применению метода моделирования значительно усиливаются возможности конкретного количественного анализа; изучение многих факторов, оказывающих влияние на экономические процессы, количественная оценка последствий изменения условий развития экономических объектов и т.п.

Решение принципиально новых экономических задач. Посредством математического моделирования удается решать такие экономические задачи, которые иными средствами решить практически невозможно, например: нахождение оптимального варианта народнохозяйственного плана, имитация народнохозяйственных мероприятий, автоматизация контроля за функционированием сложных экономических объектов.

Задачи контрольной работы:

1. Математические модели процессов

2. Особенности симплексного метода

1.1 Математические модели процессов.

Математи́ческая моде́ль — это математическое представление реальности.

Математическое моделирование — процесс построения и изучения математических моделей.

Все естественные и общественные науки, использующие математический аппарат, по сути занимаются математическим моделированием: заменяют реальный объект его математической моделью и затем изучают последнюю.

Никакое определение не может в полном объёме охватить реально существующую деятельность по математическому моделированию. Несмотря на это, определения полезны тем, что в них делается попытка выделить наиболее существенные черты.

Определение модели по А. А. Ляпунову: Моделирование — это опосредованное практическое или теоретическое исследование объекта, при котором непосредственно изучается не сам интересующий нас объект, а некоторая вспомогательная искусственная или естественная система (модель):

1. находящаяся в некотором объективном соответствии с познаваемым объектом;

2. способная замещать его в определенных отношениях;

3 .дающая при её исследовании, в конечном счете, информацию о самом моделируемом объекте.

Классификация моделей

Классификация моделей

Формальная классификация моделей

Формальная классификация моделей основывается на классификации используемых математических средств. Часто строится в форме дихотомий. Например, один из популярных наборов дихотомий :

- Линейные или нелинейные модели;

- Сосредоточенные или распределённые системы;

- Детерминированные или стохастические;

- Статические или динамические;

- Дискретные или непрерывные .

и так далее. Каждая построенная модель является линейной или нелинейной, детерминированной или стохастической, … Естественно, что возможны и смешанные типы: в одном отношении сосредоточенные (по части параметров), в другом — распределённые модели и т. д.

Классификация по способу представления объекта

Наряду с формальной классификацией, модели различаются по способу представления объекта:

-Структурные или функциональные модели

Содержательные и формальные модели

Практически все авторы, описывающие процесс математического моделирования, указывают, что сначала строится особая идеальная конструкция, содержательная модель[. Устоявшейся терминологии здесь нет, и другие авторы называют этот идеальный объект концептуальная модель, умозрительная модель или предмодель. При этом финальная математическая конструкция называется формальной моделью или просто математической моделью, полученной в результате формализации данной содержательной модели (предмодели). Построение содержательной модели может производиться с помощью набора готовых идеализаций, как в механике, где идеальные пружины, твёрдые тела, идеальные маятники, упругие среды и т. п. дают готовые структурные элементы для содержательного моделирования. Однако в областях знания, где не существует полностью завершенных формализованных теорий (передний край физики, биологии, экономики, социологии, психологии, и большинства других областей), создание содержательных моделей резко усложняется.

Содержательная классификация моделей

В работе Р. Пайерлса дана классификация математических моделей, используемых в физике и, шире, в естественных науках. В книге А. Н. Горбаня и Р. Г. Хлебопроса эта классификация проанализирована и расширена. Эта классификация сфокусирована, в первую очередь, на этапе построения содержательной модели.

Тип 1 : Гипотеза (такое могло бы быть)

Никакая гипотеза в науке не бывает доказана раз и навсегда. Очень чётко это сформулировал Ричард Фейнман:

Если модель первого типа построена, то это означает что она временно признаётся за истину и можно сконцентрироваться на других проблемах. Однако это не может быть точкой в исследованиях, но только вре́менной паузой: статус модели первого типа может быть только вре́менным.

Тип 2: Феноменологическая модель (ведем себя так, как если бы…)

Роль модели в исследовании может меняться со временем, может случиться так, что новые данные и теории подтвердят феноменологические модели и те будут повышены до статуса гипотезы. Аналогично, новое знание может постепенно прийти в противоречие с моделями-гипотезами первого типа и те могут быть переведены во второй. Так, кварковая модель постепенно переходит в разряд гипотез; атомизм в физике возник как временное решение, но с ходом истории перешёл в первый тип. А вот модели эфира, проделали путь от типа 1 к типу 2, а сейчас находятся вне науки.

Идея упрощения очень популярна при построении моделей. Но упрощение бывает разным. Пайерлс выделяет три типа упрощений в моделировании.

Тип 3: Приближение (что-то считаем очень большим или очень малым)

Если можно построить уравнения, описывающие исследуемую систему, то это не значит, что их можно решить даже с помощью компьютера. Общепринятый прием в этом случае — использование приближений (моделей типа 3). Среди них модели линейного отклика. Уравнения заменяются линейными. Стандартный пример — закон Ома.

Если мы используем модель идеального газа для описания достаточно разреженных газов, то это — модель типа 3 (приближение). При более высоких плотностях газа тоже полезно представлять себе более простую ситуацию с идеальным газом для качественного понимания и оценок, но тогда это уже тип 4.

Тип 4: Упрощение (опустим для ясности некоторые детали)

Примеры: применение модели идеального газа к неидеальному, уравнение состояния Ван-дер-Ваальса, большинство моделей физики твердого тела, жидкостей и ядерной физики. Путь от микроописания к свойствам тел (или сред), состоящих из большого числа частиц, очень длинен. Приходится отбрасывать многие детали. Это приводит к моделям 4-го типа.

Тип 5 : Эвристическая модель (количественного подтверждения нет, но модель способствует более глубокому проникновению в суть дела)

Но при построении новой физики далеко не сразу получается модель, дающая хотя бы качественное описание объекта — модель пятого типа. В этом случае часто используют модель по аналогии, отражающую действительность хоть в какой-нибудь черте.

Тип 6: Аналогия (учтём только некоторые особенности)

Тип 7: Мысленный эксперимент (главное состоит в опровержении возможности)

А. Эйнштейн был одним из великих мастеров мысленного эксперимента. Вот один из его экспериментов. Он был придуман в юности и, в конце концов, привел к построению специальной теории относительности. Предположим, что в классической физике мы движемся за световой волной со скоростью света. Мы будем наблюдать периодически меняющееся в пространстве и постоянное во времени электромагнитное поле. Согласно уравнениям Максвелла, этого быть не может. Отсюда юный Эйнштейн заключил: либо законы природы меняются при смене системы отсчета, либо скорость света не зависит от системы отсчета. Он выбрал второй — более красивый вариант. Другой знаменитый мысленный эксперимент Эйнштейна — Парадокс Эйнштейна — Подольского — Розена.

А вот и тип 8, широко распространенный в математических моделях биологических систем.

Тип 8: Демонстрация возможности (главное — показать внутреннюю непротиворечивость возможности)

Это тоже мысленные эксперименты с воображаемыми сущностями, демонстрирующие, что предполагаемое явление согласуется с базовыми принципам и внутренне непротиворечиво. В этом основное отличие от моделей типа 7, которые вскрывают скрытые противоречия.

В основе содержательной классификации — этапы, предшествующие математическому анализу и вычислениям. Восемь типов моделей по Р. Пайерлсу суть восемь типов исследовательских позиций при моделировании.

Рассмотрим механическую систему, состоящую из пружины, закрепленной с одного конца, и груза массой m, прикрепленного к свободному концу пружины. Будем считать, что груз может двигаться только в направлении оси пружины (например, движение происходит вдоль стержня). Построим математическую модель этой системы. Будем описывать состояние системы расстоянием x от центра груза до его положения равновесия. Опишем взаимодействие пружины и груза с помощью закона Гука (F = − kx) после чего воспользуемся вторым законом Ньютона, чтобы выразить его в форме дифференциального уравнения:

где означает вторую производную от x по времени: .

По формальной классификации эта модель линейная, детерминисткая, динамическая, сосредоточенная, непрерывная. В процессе её построения мы сделали множество допущений (об отсутствии внешних сил, отсутствии трения, малости отклонений и т. д.), которые в реальности могут не выполняться.

Жёсткие и мягкие модели

Здесь — некоторая функция, в которой может учитываться сила трения или зависимость коэффициента жёсткости пружины от степени её растяжения, — некоторый малый параметр. Явный вид функции f нас в данный момент не интересует. Если мы докажем, что поведение мягкой модели принципиально не отличается от поведения жёсткой (вне зависимости от явного вида возмущающих факторов, если они достаточно малы), задача сведется к исследованию жёсткой модели. В противном случае применение результатов, полученных при изучении жёсткой модели, потребует дополнительных исследований. Например, решением уравнения гармонического осциллятора являются функции вида , то есть колебания с постоянной амплитудой. Следует ли из этого, что реальный осциллятор будет бесконечно долго колебаться с постоянной амплитудой? Нет, поскольку рассматривая систему со сколь угодно малым трением (всегда присутствующим в реальной системе), мы получим затухающие колебания. Поведение системы качественно изменилось.

Если система сохраняет свое качественное поведение при малом возмущении, говорят, что она структурно устойчива. Гармонический осциллятор — пример структурно-неустойчивой (негрубой) системы.Тем не менее, эту модель можно применять для изучения процессов на ограниченных промежутках времени

Универсальность моделей

Прямая и обратная задачи математического моделирования

Существует множество задач, связанных с математическим моделированием. Во-первых, надо придумать основную схему моделируемого объекта, воспроизвести его в рамках идеализаций данной науки. Так, вагон поезда превращается в систему пластин и более сложных тел из разных материалов, каждый материал задается как его стандартная механическая идеализация (плотность, модули упругости, стандартные прочностные характеристики), после чего составляются уравнения, по дороге какие-то детали отбрасываются, как несущественные, производятся расчёты, сравниваются с измерениями, модель уточняется, и так далее. Однако для разработки технологий математического моделирования полезно разобрать этот процесс на основные составные элементы.

Традиционно выделяют два основных класса задач, связанных с математическими моделями: прямые и обратные.

Прямая задача : структура модели и все её параметры считаются известными, главная задача — провести исследование модели для извлечения полезного знания об объекте. Какую статическую нагрузку выдержит мост? Как он будет реагировать на динамическую нагрузку (например, на марш роты солдат, или на прохождение поезда на различной скорости), как самолёт преодолеет звуковой барьер, не развалится ли он от флаттера, — вот типичные примеры прямой задачи. Постановка правильной прямой задачи (задание правильного вопроса) требует специального мастерства. Если не заданы правильные вопросы, то мост может обрушиться, даже если была построена хорошая модель для его поведения. Так, в 1879 г. в Великобритании обрушился металлический мост через реку Тей, конструкторы которого построили модель моста, рассчитали его на 20-кратный запас прочности на действие полезной нагрузки, но забыли о постоянно дующих в тех местах ветрах. И через полтора года он рухнул.

В простейшем случае (одно уравнение осциллятора, например) прямая задача очень проста и сводится к явному решению этого уравнения.

Обратная задача: известно множество возможных моделей, надо выбрать конкретную модель на основании дополнительных данных об объекте. Чаще всего, структура модели известна, и необходимо определить некоторые неизвестные параметры. Дополнительная информация может состоять в дополнительных эмпирических данных, или в требованиях к объекту (задача проектирования). Дополнительные данные могут поступать независимо от процесса решения обратной задачи (пассивное наблюдение) или быть результатом специально планируемого в ходе решения эксперимента (активное наблюдение).

Одним из первых примеров виртуозного решения обратной задачи с максимально полным использованием доступных данных был построенный И. Ньютоном метод восстановления сил трения по наблюдаемым затухающим колебаниям.

В качестве другого примера можно привести математическую статистику. Задача этой науки — разработка методов регистрации, описания и анализа данных наблюдений и экспериментов с целью построения вероятностных моделей массовых случайных явлений. Т.е. множество возможных моделей ограничено вероятностными моделями. В конкретных задачах множество моделей ограничено сильнее.

Компьютерные системы моделирования

Для поддержки математического моделирования разработаны системы компьютерной математики, например, Maple, Mathematica, Mathcad, MATLAB, VisSim и др.Они позволяют создавать формальные и блочные модели как простых, так и сложных процессов и устройств и легко менять параметры моделей в ходе моделирования. Блочные модели представлены блоками (чаще всего графическими), набор и соединение которых задаются диаграммой модели.

1.2 Особенности симплекс метода

Симплекс-метод позволяет отказаться от метода перебора при решении задач линейной оптимизации, является основным численным методом решения задач линейного программирования и позволяет за меньшее число шагов, чем в методе перебора, получить решение.

Реализация алгоритма симплекс-метода.

Записать задачу в канонической форме: заменить все ограничения-неравенства с положительной правой;
Разделить переменные на базисные и свободные: перенести свободные переменные в правую часть ограничений-неравенств.
Выразить базисные переменные через свободные: решить систему линейных уравнений (ограничений-неравенств) – относительно базисных переменных;
Проверить неотрицательность базисных переменных: убедиться в неотрицательности свободных членов в выражениях для базисных переменных. Если это не так, вернуться к пункту 2, выбирая другой вариант разделения переменных на базисные и свободные.
Выразить функцию цели через свободные переменные: базисные переменные, входящие в функцию, выразить через свободные переменные;
Вычислить полученное базисное решение и функцию цели на нем: приравнять к 0 свободные переменные;
проанализировать формулу функции цели: если все коэффициенты свободных переменных положительны (отрицательны), то найденное базисное решение будет минимально (максимально) и задача считается решенной;
Определить включаемую в базис и исключаемую из базиса переменные: если не все коэффициенты при свободных переменных в функции цели положительны (отрицательны), то следует выбрать свободную переменную, входящую в функцию цели с максимальным по модулю отрицательным (положительным) коэффициентом, и увеличивать ее до тех пор, пока какая-нибудь из базисных переменных не станет равной 0. Свободную переменную рассматриваем как новую базисную переменную (включаемую в базис), а базисную переменную рассматриваем как новую базисную переменную (исключаемую из базиса);
Используя новое разделение переменных на базисное и свободное, вернуться к пункту 3 и повторять все этапы до тех пор, пока не будет найдено оптимальное решение.

Для привидения системы ограничений неравенств к каноническому виду, необходимо в системе ограничений выделить единичный базис.

Алгоритм симплекс метода .

(первая симплекс таблица)

Пусть система приведена к каноническому виду.

X1+ q1,m+1 Xm+1 + …. + q1,m+nXm+n = h1

X2+ q1,m+1 Xm+1 + …. + q1,m+nXm+n = h1

X3+ q1,m+1 Xm+1 + …. + q1,m+nXm+n = h1

Xm+ qm,m+1 Xm+1 + …. + qm,m+nXm+n =hm

В ней m базисных переменных, k свободных переменных. m+k=n - всего переменных.

Fmin= C1X1+ C2X2+ C3X3+. + CnXn

Все hi должны быть больше либо равны нулю, где i=1,2. m. На первом шаге в качестве допустимого решения принимаем все Xj=0 (j=m+1,m+2. m+k). При этом все базисные переменные Xi=Hi.

Для дальнейших рассуждений вычислений будем пользоваться первой симплекс таблицей (таблица 3.1).

Напомним, что математическая модель установившегося режима (иначе — статическая характеристика элемента или системы) отражает функциональную связь между входными и выходными величинами в установившемся состоянии, а математическая модель переходного режима (динамическая характеристика элемента или системы) описывает изменение выходной величины во времени в зависимости от изменения входной величины.

Как уравнения статики, так и уравнения динамики могут быть линейными или нелинейными, в последнем случае они подлежат линеаризации.

где F — некоторая нелинейная функция; n, т, l — целые натуральные числа, определяющие наивысший порядок входящих в уравнение производных входной и выходной величин по времени.

Для реальных систем порядок дифференциального уравнения n > т и n > l. Линеаризацию нелинейных дифференциальных уравнений осуществляют методом малых отклонений. При этом вместо абсолютного значения переменных в уравнении (3.1) используют их отклонения от начального значения

В результате уравнение (3.1) становится линейным ипри одной входной величине может быть записано в виде

Линеаризация уравнений статики.Уравнения статики элементов (систем) автоматического управления, как правило, нелинейные и могут быть представлены в виде кривой или ломаной линии.

Линеаризация нелинейных статических характеристик осуществляется несколькими способами.

Метод малых отклонений. Основан на разложении аналитической функции в ряд Тейлора и отбрасывании малозначащих членов.

Таким образом, линеаризованное уравнение , где ; .

Метод касательной (рис. 3.1, а). Основан на замене участка кривой прямой линией, касательной к этой кривой в точке А (х₀, у₀), называемой рабочей точкой и находящейся в середине рабочего диапазона изменения . Как и в предыдущем случае, линеаризованное уравнение , где .

Метод секущей. Основан на замене уравнения нелинейной характеристики уравнением секущей, параметры которого определяют методом наименьших квадратов.

Первый из рассмотренных методов применяют, когда статическая характеристика задана аналитически, второй и третий — графически.

Встречаются элементы автоматической СУ, статические характеристики которых не поддаются линеаризации указанными ранее методами. Эти характеристики называют существенно нелинейными.

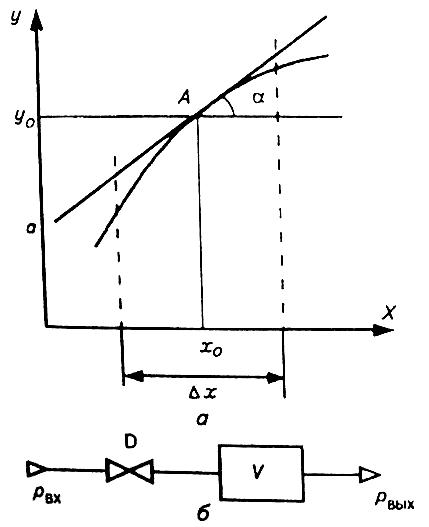
Рис. 3.1. Линеаризация статической характеристики (а) и модель пневматической камеры (б)

В результате уравнение (3.1) становится линейным ипри одной входной величине может быть записано в виде

Линеаризация нелинейных статических характеристик осуществляется несколькими способами.

Таким образом, линеаризованное уравнение , где ; .

Рис. 3.1. Линеаризация статической характеристики (а) и модель пневматической камеры (б)

Эффективность применения современных силовых устройств гибкого регулирования (FACTS), основанных на широком применении преобразовательной техники, предлагается выполнять на базе простых моделей, с приемлемой точностью воспроизводящих их внешние характеристики. Более подробно были рассмотрены модели двух устройств: СТАТКОМа и ОРПМ. Моделирование СТК двустороннего действия и УШР, включающего в свой состав нерегулируемую батарею конденсаторов, произведено с помощью управляемой проводимости, с учетом запаздывания в случае необходимости. Полученные результаты используются только для сравнения.

Математическая модель СТАТКОМ

Электромеханические переходные процессы электроэнергетической системы с учетом регулируемого устройства типа СТАТКОМ могут быть определены из следующей динамической модели, описанной системой алгебро-дифференциальных уравнений.

Проводимость СТАТКОМа, соответствующая, как и ранее, индуктивным сопротивлениям согласующего трансформатора и сглаживающего реактора (xΣ= 0,2), принимается в относительных единицах равной

Мощность СТАТКОМа S_ст задается в исходных данных.

Приращение ЭДС СТАТКОМа ΔE_ст вычисляется на основе следующей передаточной функции:

где U_уст — напряжение уставки,

K_st–коэффициент регулированияканала отклонения напряжения (K_st = -1…-10),

T_v — постоянная времени канала отклонения напряжения (Tv = 0,001 с).

Величина приращения ЭДС ограничивается на уровне 0,2 о.е., следовательно, модуль тока СТАТКОМа, равный произведению ∆𝐸ст ∙ 𝑏ст не может превысить заданной в относительных единицах величины Sст.

Поскольку при моделировании используется общая координатная система q,d, связанная с математической моделью генератора, то вычисляются коэффициенты распределения приращения ЭДС по осям q и d:

D, q — составляющие токов СТАТКОМа вычисляются в соответствии с соотношениями, связывающими составляющие его ЭДС и напряжения на его зажимах:

откуда следует, что

Выражения в круглых скобках представляют собой проекции приращений ЭДС СТАТКОМа соответственно на d и q координатные оси, поэтому q,d — составляющие токов вычисляются по выражениям:

Непосредственное использованиерезультатов вычисления токов по алгебраическим выражениям, в балансе токов в узле подключения СТАТКОМа приводит к вычислительной неустойчивости, поэтому значения, участвующие в вычислительном процессе, определяются с помощью передаточных функций:

где T_i — постоянная времени, определяющая запаздывание реакции СТАТКОМа на изменение управляющего воздействия по каналу регулирования ЭДС, обычное значение T_i = 0,0033…0,01 с.

Математическая модель ПСТАТКОМа

Для выполнения расчетов электромеханических переходных процессов электроэнергетической системы с учетом регулируемого устройства типа ПСТАТКОМ может быть предложена следующая динамическая модель, описываемая системой алгебро-дифференциальных уравнений. Предполагается, что устройство работает в составе объединенного регулятора перетока мощности (ОРПМ), включающего в себя СТАТКОМ, который передает ПСТАТКОМу определенную величину активной мощности (в соответствии с собственным режимом работы). Совместная работа двух устройств отражена в системе ограничений с учетом возможности независимой генерации устройствами реактивных мощностей.

Индуктивное сопротивление трансформатора ПСТАТКОМа принимается в относительных единицах равным x_пст = 0,04 …0,1 о.е.

Мощность ПСТАТКОМа S_ст задается в исходных данных.

Сигнал управления ЭДС ПСТАТКОМа вычисляется по известному отклонению тока с помощью следующей передаточной функции:

где Iуст — ток уставки,

K_0i — коэффициент регулированияканала отклонения тока (K_0i = -1…-10),

T_i — постоянная времени канала отклонения тока (T_i = 0,01 с).

D, q — составляющие ЭДС ПСТАТКОМа вычисляются с использованием передаточных функций с учетом дополнительного сигнала управления по отклонению скольжения s ротора генератора относительно синхронной оси:

$C:\Users\Евгений\Desktop\Практика\Снимок2.PNG$

Величины приращений добавочных напряжений ПСТАТКОМа вычисляются по полученным составляющим ЭДС с учетом ограничений, определяемых возможностями передачи мощности от СТАТКОМа в соответствии с его загрузкой; ограничивается на уровне разности комплексных мощностей S_пст=|S_{ст_max} — S_cт|, таким образом, приращения напряжений, вносимые ПСТАТКОМом, не превышают заданных величин, соответствующих мощности S_{пст_max} и величине мощности, поступающей со стороны СТАТКОМа. Для этого рассчитываются коэффициенты распределения в координатной системе q,d:

D, q — составляющие напряжений ПСТАТКОМа вычисляются в соответствии с ограничениями:

$C:\Users\Евгений\Desktop\Практика\Снимок.PNG$

Непосредственное использование результатов вычисления составляющих напряжения по алгебраическим выражениям в балансе напряжений в узле подключения ПСТАТКОМа приводит к вычислительной неустойчивости, поэтому значения, участвующие в вычислительном процессе, определяются с помощью передаточных функций:

где T_u — постоянная времени, определяющая запаздывание реакции ПСТАТКОМа на изменение управляющего воздействия по каналу регулирования ЭДС, обычное значение T_i = 0,0033…0,01 с.

Заключение

В основу разработанных методов математического моделирования положено воспроизведение внешних характеристик рассматриваемых устройств FACTS.

Разработана методика расчета характеристик мощности электропередачи с компенсирующими устройствами типа СТАТКОМ и ОРПМ для сравнения эффективности влияния устройств FACTS на режимы работы энергосистем. В методике учтены ограничения по режиму напряжения в точке подключения устройства к сети и ограничения тока преобразователя СТАТКОМа (ОРПМ) при изменении угла δ.

Разработаны математические модели двух основных устройств FACTS — СТАТКОМа и ОРПМ (в составе СТАТКОМа и ПСТАТКОМа). Модели могут использоваться в составе любого программного комплекса, предназначенного для расчетов электромеханических переходных процессов.

Основные термины (генерируются автоматически): FACTS, подключение устройства, вычислительная неустойчивость, вычислительный процесс, динамическая модель, математическая модель, общая координатная система, обычное значение, передаточная функция, электроэнергетическая система.

Математические модели переходных процессов доклад

Похожие статьи

Исследование влияния параметров системы АРВ на переходные.

Аналитический обзор методов анализа переходных процессов.

Управление линейной динамической системой в условиях.

Комплект математических моделей компонентов судовых.

Построение АФЧХ системы автоматического регулирования.

Анализ передаточной функции структурной схемы вентильного.

О непараметрическом алгоритме моделирования нелинейных.

Математическая модель асинхронного двигателя в неподвижной.

Математическая модель асинхронного двигателя с переменными.