Конус доклад по геометрии 9 класс

Обновлено: 18.05.2024

* Данная работа не является научным трудом, не является выпускной квалификационной работой и представляет собой результат обработки, структурирования и форматирования собранной информации, предназначенной для использования в качестве источника материала при самостоятельной подготовки учебных работ.

Определение и свойства конуса.

Форму конуса (приближено) имеют терриконы и вулканы, воронки и колбы, кульки и кучи песка и т.д. В геометрии же конус, как и цилиндр, определяют как фигуру, образованную отрезками.

Пусть дана плоская фигура F и некоторая точка P, не лежащая с фигурой F в одной плоскости. Отрезки, проведенные из точки P во все точки фигуры F, образуют фигуру, которую называют конусом (рис.1).

Точка P называется вершиной конуса, а фигура F – основанием конуса. Отрезки, соединяющие вершину конуса с точками его основания, называются, образующими конуса. Высотой конуса называется перпендикуляр из вершины конуса на плоскость его основания, а также длина этого перпендикуляра.

Конусом называют также фигуры, образованные лучами, идущими из точки Р через точки фигуры F и точку Р.

Около конуса шар можно описать всегда. Центром шара является центр окружности, описанной около осевого сечения конуса. Радиус шара R=F сопоставим точку X'F', в которой отрезок PX пересекает плоскость ?'.

Проведем высоту PA конуса K и пусть A' – точка, в которой высота PA пересекает плоскость ?'. Отрезок PA' является высотой конуса K', отсеченного плоскостью ?'.

Возьмем любые две точки X, Y основания F и пусть X', Y' – соответствующие им точки F'. Рассмотрим треугольники PXY и PX'Y'. Они подобны, так как отрезки X'Y' и XY параллельны (поскольку плоскость PXY пересекает параллельные плоскости ? и ?' по параллельным прямым). Поэтому

Теперь рассмотрим треугольники PAX и PA'X'. Они также подобны и потому

Из неравенства (1) и (2) следует, что X'Y':XY= PA':PA, а это и означает подобие фигур F' и F с коэффициентом k = PA':PA.

Рассмотрим конус, у которого основания круг, а вершина P проектируется в центре O его основания.

Как следует из теоремы о сечении конуса, в пересечении такого конуса с плоскостями, параллельными плоскости его основания (и, тем самым, перпендикулярными его высоте PO), получаются круги с центрами на высоте PO. Следовательно, рассматриваемый конус является фигурой вращения: его высота и есть его ось вращения. Поэтому такой конус называют конусом вращения.

Итак, конусом вращения называется конус, основание которого – круг и вершина которого проектируется в центре основания.

Осевые сечения конуса вращения – это его сечения плоскостями, проходящими через его ось. Все такие сечения представляют собой равнобедренные треугольники, поскольку вершина конуса вращения равноудалена от всех точек окружности его основания.

Любая плоскость, проходящая через ось конуса вращения, является его плоскостью симметрии.

Фигура, состоящая из тех образующих конуса вращения, которые соединяют его вершину с окружностью основания, называется боковой поверхностью конуса вращения. Она сама является конусом вращения с той же вершиной, основанием которого служит окружностью основания исходного конуса вращения. Все образующие, лежащие на боковой поверхности конуса вращения, равнонаклонены к плоскости его основания.

Поверхность конуса вращения состоит из его основания и его боковой поверхности. (Поверхность конуса вращения называют также его полной поверхностью).

Высотой усеченного конуса называется перпендикуляр, опущенный из точки одного основания на плоскость другого. Все такие перпендикуляры равны. Высотой называют также их длину, т.е. расстояние между плоскостями оснований.

Усеченный конус вращения получается из конуса вращения. Поэтому его основания и все параллельные им его сечения – круги с центрами на одной прямой – на оси. Усеченный конус вращения получается вращением прямоугольной трапеции вокруг её боковой стороны, перпендикулярной основаниям, или вращением равнобедренной трапеции вокруг оси симметрии.

Боковая поверхность усеченного конуса вращения – это принадлежащая ему часть боковой поверхности конуса вращения, из которого он получен. Поверхность усеченного конуса вращения (или его полная поверхность) состоит из его оснований и его боковой поверхности.

Площадь поверхности конуса.

Боковую поверхность конуса, как и боковую поверхность цилиндра, можно развернуть на плоскость, разрезав её по одной из образующих (рис. 3, а, в). Разверткой боковой поверхности конуса является круговой сектор (рис.3, б), радиус которого равен образующей конуса, а длина дуги сектора – длине окружности основания конуса.

За площадь боковой поверхности конуса принимается площадь её развертки. Выразив площадь S_бок боковой поверхности конуса через его образующую l и радиус основания r. Площадь кругового сектора – развертки боковой поверхности конуса (рис. 3, б) – равна - градусная мера дуги АВА', поэтому

рис. 3, а рис. 3, б

S_бок = через l и r. Так как длина дуги АВА' равна 2?r (длине окружности основания конуса), то 2?r = (см 2 )

Ответ: S_АВС = 25(см 2 )

Образующая конуса равна l, а радиус основания равен r. Найдите площадь сечения, проходящего через вершину конуса и хорду основания, стягивающую дугу в 60°.

В АОК = 60°, тогда ;

S = = == =60°.
р – полупериметр.

V = S_осн · h; V = = 3(см); S = 9? (см 2 ).

Площадь осевого сечения конуса равна 0,6см 2 . Высота конуса равна 1,2 см. Вычислите площадь полной поверхности конуса.

Осевым сечением конуса является равнобедренный треугольник АВС, АВ = ВС = l.

АС = 2r; S_сеч = ; l = = 1,3(см)

S_полн = ?r (r+l); S_полн = ? 0,5(0,5 + 1,3) = 0,9? (см 2 ).

О данной геометрической фигуре пойдёт речь в сегодняшней статье.

Определение и элементы конуса

Под конусом понимают тело, состоящее из круга и точки, которая удалена от его поверхности на определённое расстояние.

При этом точка соединяется с основанием посредством проведения лучей, которые называются образующими. Линия, соединяющая центр круга с удалённой точкой, является высотой данной фигуры.

Обратите внимание! Также существует такое понятие, как ось конуса. Это линия, проходящая через его центр и совпадающая с высотой. Образующие строятся относительно оси.

Хотелось бы рассмотреть ещё несколько понятий по этой теме:

1. Под конусностью понимают отношение диаметра основания фигуры и её высоты:

Важно! Конусность отвечает за угол наклона образующих. Чем больше данный параметр, тем острее угол.

2. Осевое сечение предполагает наличие плоскости, которая будет рассекать фигуру, проходя через ось:

3. Касательная— это плоскость, которая соприкасается с образующей конуса. При этом важно, чтобы она была перпендикулярна осевому сечению.

Свойства кругового конуса

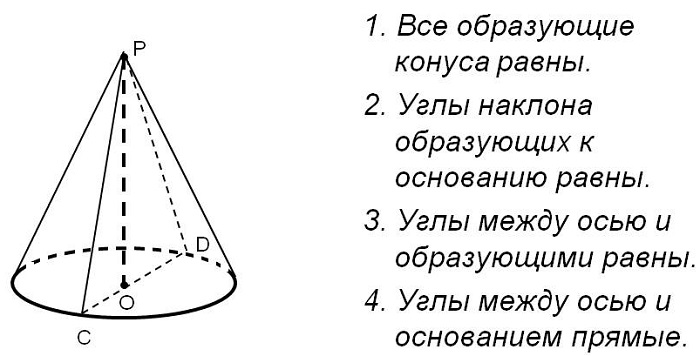
Выделяют несколько особенностей, которыми обладает фигура данного типа:

Образующие кругового конуса равны друг другу.

Чтобы найти центр тяжести фигуры, нужно её высоту поделить на четыре части.

Место пересечения плоскости сечения и основы образует параболу. Если через вершину тела провести плоскость сечения, то получится равнобедренный треугольник.

Интересный факт! Если вращать прямоугольный треугольник вокруг одного из катетов, то получится конус. При этом важно, чтобы угол вращения был не менее 360 градусов.

Общая формула объёма фигуры

Чтобы найти объём кругового конуса, необходимо умножить число Пи на его высоту, на радиус в квадрате и всё это произведение поделить на три:

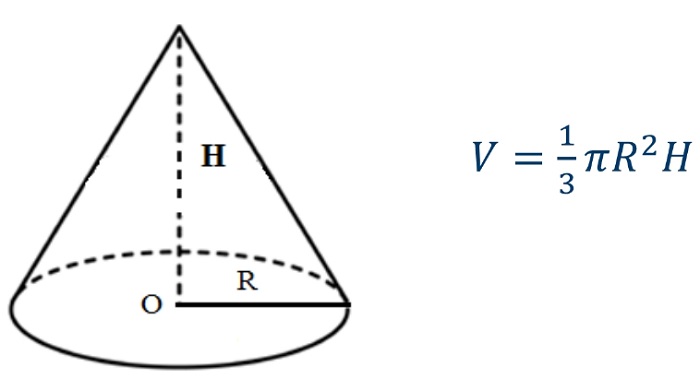
Дополнительная информация! Чтобы узнать объём фигуры, нужно умножить площадь её основы на высоту и поделить на три:

Объём усечённого конуса

Это часть прямого конуса, которая находится в пространстве между основой и плоскостью, параллельной этому основанию. В общем виде выглядит следующим образом:

Объём данного тела можно вычислить по формуле:

Важно! S и S ₁ это площади соответствующих основ, которые равняются ПR 2 и ПR ₁ 2 При нахождении этих значений поможет онлайн калькулятор.

Площадь поверхности фигуры

Для вычисления данного параметра потребуется знать площадь боковой поверхности. Она равняется произведению числа π, радиуса и длины образующей.

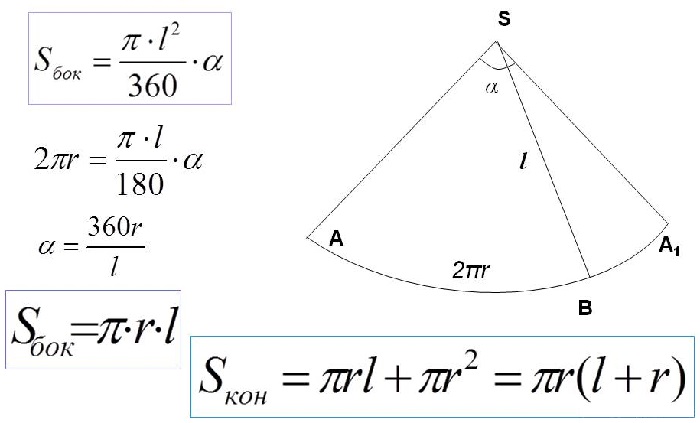
Чтобы рассчитать площадь всей поверхности, нужно сложить площади его основы и боковой поверхности.

Площадь усечённого конуса

Для нахождения данного параметра нужно воспользоваться формулами:

площади боковой поверхности усечённого конуса S_бок;

полной площади усечённой фигуры S_пол, которая равна сумме площадей двух оснований и площади боковой поверхности:

Здесь l - длина образующей, а R и r - радиусы большего и меньшего оснований соответственно.

Уравнение конуса

Часто требуется при решении математических задач. Записывается в следующем виде:

где x₀, y_0,z₀- координаты по соответствующим осям.

В данной публикации мы рассмотрим определение, основные элементы и виды одной из самых распространенных фигур в пространстве – конуса. Представленная информация сопровождается соответствующими рисунками для лучшего восприятия.

Определение конуса

Далее мы будем рассматривать самый распространенный вид конуса – прямой круговой. Остальные возможные варианты фигуры перечислены в последнем разделе публикации.

Итак, прямой круговой конус – это трехмерная геометрическая фигура, полученная путем вращения прямоугольного треугольника вокруг одного из своих катетов, который в данном случае будет являться осью фигуры. Ввиду этого иногда такой конус называют конусом вращения.

Конус на рисунке выше получен в результате вращения прямоугольного треугольника ACD (или BCD) вокруг катета CD.

Основные элементы конуса

R – радиус круга, являющегося основанием конуса. Центр круга – точка D, диаметр – отрезок AB.
h (CD) – высота конуса, одновременно являющаяся осью фигуры и катетом прямоугольных треугольников ACD или BCD.
Точка C – вершина конуса.
l (CA, CB, CL и CM) – образующие конуса; это отрезки, соединяющие вершину конуса с точками на окружности его основания.

Между образующей конуса, его высотой и радиусом основания есть взаимосвязь (согласно теореме Пифагора):

Развёртка конуса – боковая поверхность конуса, развернутая в плоскость; является круговым сектором.

2πR

α – угол развёртки (или центральный угол);
l – радиус сектора.

Примечание: Основные свойства конуса мы рассмотрели в отдельной публикации.

Конус – тело, полученное вращением прямоугольного треугольника вокруг прямой, содержащей катет.

S- вершина конуса, круг с центром О – основание конуса

Отрезок SA=L образующая.

Отрезок OA=R – радиус основания.

Отрезок BC=2R – диаметр основания.

Треугольник SBC-осевое сечение

Угол BSC – угол при вершине осевого сечения

Угол SBO – угол наклона образующей к плоскости основания

II Сечение конуса

1. Секущая плоскость проходит через ось конуса (осевое сечение – равнобедренный треугольник рис. 1)

2. Секущая плоскость проходит перпендикулярно к оси конуса

- круг с центром О1 (рис. 2)

3.Сечение проходящее через верщину конуса – равнобедренный

треугольник (рис. 3)

4.Параболическое и гиперболическое сечения. (рис. 4 )

В конус всегда можно вписать шар. Его центр на оси конуса

и совпадает с центром окружности, вписанно в треугольник,

являющийся осевым сечением конуса.

Rш= Rк * tg a/2 = H*Rк/Rк+L

Около конуса всегда можно описать шар. Его центр лежит на

оси конуса и совпадает с центром окружности, описаной около

треугольника, являющегося осевым сечением конуса.

Rш = Rк / sinb ; R²ш= (H-Rш) ² + Rк²

Rш =L/2H ; (2Rш - Hк)Hк = Rк²

III Площадь поверхности конуса

1. За плщадь боковой поверхности конуса принимается площадь её разертки. Выразим S бок через его опразующую L и радиус основания r. Площадь кругового сектора πL²/360*α . Выразим α через L и r . Длинна дуги ABA равна 2πr (длинна окружности основания конуса) 2πr = πL/180* α, откуда следует α=360r/L следовательно Sбок = πL²360r/360L=πrL

2. Площадь полной поверхности конуса есть сумма площадей боковой поверхности и основания

IV Объем конуса

Объем конуса равен одной трети произведения площади основания на высоту.

Рассмотрим конус с обьемом V, радиусом R, высотой h и вершиной О. Введем ось Ох, чтобы она совпадала с осью конуса -ОН . Произвольное сечение конуса плоскостью, перпендикулярной к оси Ох, является круг с центром в точке Н1 пересечения этой плоскости с осью Ох. Обозначим Радиус этого круга через , ф площадь S(x) через,где х-абсцисса точки Н1. Из подобия треугольников ОН1А1 и ОНА следует,что ОН1/ОН=R1/R,

или x/h=R1/R =>R1=XR/h. Так как S(x)= πR², то S(x)= πR²/h²* ²

Применяя основную формулу вычисления обьемов тел при а=0 и b=h получаем

V Усеченный конус.

Усеченный конус – часть конуса, заключенная между основанием и паралельным основанию сечением конуса.

Круги с центрами О1 и О2 – верхнее и нижнее основания усеченного конуса, R r – радиусы оснований, АВ= L образующая ,α угол наклона образующе и плоскости нижнего основания.

Отрезок О1О2-высота. Трапеция АВСD – осевое сечение.

Н=L*sinα

Около усеченного конуса всегда можно описать шар. Его центр лежит на прямой О1О2

О – центр описанного шара R - радиус описанного шара, равный радиусу окружносит описанной около ΔACD

В усеченный конус можно вписать шар тогда и только тогда, когда образующая равна сумме радиусов оснований L=R+r => существует вписанный шар.

VI Площадь поверхности усеченного конуса

1. Пусть Р – вершина конуса, из которого получен усеченный конус, АА1-одна из образующих

Усеченного конуса О и О1 – центры оснований. Используя формулу Sбок для конуса получаем

S бок = πr*PA-πr1*PA1=πr(PA1+AA1)- πr1PA1, отсюда, учитывая, что AA1=L, находим

Sбок =πrL +π (r - r1)PA1

Выразим РА1 через L1, r и r1. Прямоугольные треугольники РО1А1 и РОА подобны, так как имеют общий острый угол Р и поэтому PA1/PA=r/r1 или PA1/PA1+L=r/R1. Получаем PA1=Lr1/R-r1. S=πrL + (π(r-r1)Lr1)/r-r1=πrL+πr1L=πL(r+r1)

2. Площадь полной поверхности усеченного конуса равна сумме площадей боковой поверхности усеченного конуса и оснований

Sполн = S1+S2+Sбок=πL(r+r1)+ πR²+πr²

VII Обьем усеченного конуса

Обьем усеченного конуса V, высота которого равна h, а площади оснований S и S1 вычисляется по формуле

Читайте также: