Геометрия евклида как первая научная система доклад

Обновлено: 05.07.2024

Исторический обзор обоснования геометрии.Геометрия, прежде чем стать аксиоматической теорией, прошла долгий путь эмпирического развития.

Греческий период развития геометрии начался в VII-VI вв. до н.э. под влиянием египтян. Отцом греческой математики считается знаменитый философ Фалес (640-548 гг. до н.э.). Фалесу, точнее, его математической школе принадлежат доказательства свойств равнобедренного треугольника, вертикальных углов. В дальнейшем геометром Древней Греции были получены результаты, охватывающие почти все содержание современного школьного курса геометрии.

Философская школа Пифагора (570-471 гг. до н.э.) открыла теорему о сумме углов треугольника, доказала теорему Пифагора, установила существование пяти типов правильных многогранников и несоизмеримых отрезков. Демокрит (470-370 гг. до н.э.) открыл теоремы об объемах пирамиды и конуса. Евдокс (410-356 гг. до н.э.) создал геометрическую теорию пропорций (т.е. теорию пропорциональных чисел).

Менехм и Аполлоний изучили конические сечения. Архимед (289-212 гг. до н.э.) открыл правила вычисления площади поверхности и объема шара и других фигур. Он же нашел приближенное значение числа π.

VII-IХ – арифметика в геометрическом изложении;

X – несоизмеримые отрезки;

Каждая книга начинается с определения тех понятий, которые в ней встречаются. Например, в книге I даны 23 определения. Приведем определения первых четырех понятий:

1 Точка есть то, что не имеет частей.

2 Линия есть длина без ширины.

3 Границы линии суть точки.

4 Прямая есть такая линия, которая одинаково расположена по отношению ко всем своим точкам.

Евклид приводит предложения, принимаемые без доказательства, разделяя их на постулаты и аксиомы. Постулатов у него пять, а аксиом – семь. Вот некоторые из них:

IV И чтобы все прямые углы были равны.

V И чтобы всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними внутренние односторонние углы, сумма которых меньше двух прямых, эти прямые пересекались с той стороны, с которой эта сумма меньше двух прямых.

I Равные порознь третьему равны между собой.

II И если к равным прибавить равные, то получим равные.

VII И совмещающиеся равны.

Евклид не указал, в чем заключается различие между постулатами и аксиомами. До сих пор нет окончательного решения этого вопроса.

Евклид излагает теорию геометрии так, как требовали греческие ученые, особенно Аристотель, т.е. теоремы расположены так, что каждая следующая доказывается только на основе предыдущих. Иначе говоря, Евклид развивает геометрическую теорию строго логическим путем. В этом и заключается историческая заслуга Евклида перед наукой.

1) многие понятия включают такие, которые в свою очередь должны быть определены (например, в определениях 1-4 главы 1 используются понятия ширины, длины, границы, которые также должны быть определены);

2) список аксиом и постулатов недостаточен для построения геометрии строго логическим путем. Например, в этом списке нет аксиом порядка, без которых нельзя доказать многие теоремы геометрии; заметим, что на это обстоятельство обратил внимание Гаусс. В указанном списке отсутствуют также определения понятия движения (совмещения) и свойств движения, т.е. аксиом движения. В списке не хватает также аксиомы Архимеда (одной из двух аксиом непрерывности), которая играет важную роль в теории измерений длин отрезков, площадей фигур и объектов тел. Заметим, что на это обратил внимание современник Евклида Архимед;

Неевклидовы геометрические системы.Н.Лобачевский (1792-1856 гг.), который открыл новую геометрию – геометрию Лобачевского, также начал с попытки доказательства постулата V.

На первый взгляд этот вывод кажется недостаточно обоснованным: может быть, развивая его дальше, можно прийти к противоречию. Но этот же вопрос относится и к геометрии Евклида. Иначе говоря, обе геометрии равноправны перед вопросом о логической непротиворечивости. Дальнейшие исследования показали, что из непротиворечивости одной следует непротиворечивость другой геометрии, т.е. имеет место равноправие логических систем.

Лобачевский был первым, но не единственным, кто сделал вывод о существовании другой геометрии. Гаусс (1777-1855 гг.) высказал эту идею еще в 1816 г. в частных письмах, но в официальных публикациях заявление не сделал.

Три года спустя после публикации результатов Лобачевского (в 1829 г.), т.е. в 1832 г., вышла работа венгра Я. Бойяи (1802-1860 гг.), который в 1823 г. пришел к выводу о существовании другой геометрии, но опубликовал позже и в менее развитом, чем у Лобачевского, виде. Поэтому справедливо, что эта геометрия носит имя Лобачевского.

Общему признанию геометрии Лобачевского в значительной степени способствовали работы геометров после Лобачевского. В 1868 г. итальянский математик Э.Бельтрами (1825-1900 гг.) доказал, что на поверхности постоянной отрицательной кривизны (так называемая псевдосфера) имеет место геометрия Лобачевского. Уязвимым местом доказательства непротиворечивости геометрии Лобачевского, основанного на интерпретации Бельтрами, было то, что, как показал Д.Гильберт (1862-1943 гг.), в евклидовом пространстве не существует полной поверхности постоянной отрицательной кривизны без особенностей. Поэтому на поверхности постоянной отрицательной кривизны можно интерпретировать только часть плоской геометрии Лобачевского. Этот недостаток был устранен А.Пуанкаре (1854-1912 гг.) и Ф.Клейном (1849-1925 гг.).

Доказательство непротиворечивости геометрии Лобачевского было вместе с тем и доказательством независимости пятого постулата от остальных. Действительно, в случае зависимости геометрия Лобачевского была бы противоречивой, так как она содержала бы два взаимно исключающих утверждения.

Дальнейшие исследования евклидовой геометрии показали неполноту системы аксиом и постулатов Евклида. Исследование аксиоматики Евклида завершил в 1899 г. Гильберт.

Аксиоматика Гильберта состоит из пяти групп:

• аксиомы связи (принадлежности);

• аксиомы конгруэнтности (равенства, совпадения);

Гильберт всесторонне исследовал свою систему аксиом, показал, что она непротиворечива, если не противоречива арифметика (т.е. на самом деле доказана содержательная или так называемая внешняя непротиворечивость). Он завершил многовековые исследования геометров по обоснованию геометрии. Эта работа была высоко оценена и в 1903 г. отмечена премией имени Лобачевского.

В современном аксиоматическом изложении геометрии Евклида не всегда пользуются аксиомами Гильберта: учебники по геометрии построены на различных модификациях этой системы аксиом.

В XX в. было обнаружено, что геометрия Лобачевского не только имеет важное значение для абстрактной математики как одна из возможных геометрий, но и непосредственно связана с приложениями математики. Оказалось, что взаимосвязь пространства и времени, открытая А.Эйнштейном и другими учеными в рамках специальной теории относительности, имеет непосредственное отношение к геометрии Лобачевского.

Предмет математики

Предмет математики нельзя ни подменять формальными логическими схемами, ни низводить до уровня коллекции разрозненных фактов. Математика есть учение об общих формах, свойственных реальному бытию, она создает постоянно развивающиеся теории, пригодные для самых различных запросов естествознания и техники. Именно это позволяет применять математические методы, разработанные при решении задач одной области науки, к совершенно непохожим на них задачам, относящимся к совсем иным областям знания.

Известны два подхода к определению предмета математики. Одно определение дано Ф.Энгельсом, другое – коллективом французских математиков под общим псевдонимом Н.Бурбаки.

В конкретной содержательной аксиоматике, подобной аксиоматике Евклида, исходные понятия и аксиомы в качестве интерпретации имеют единственную систему хотя и идеализированных, но конкретных объектов. В противоположность этому абстрактная аксиоматика допускает бесчисленное множество интерпретаций. Формализованная аксиоматика возникает на основе абстрактной и отличается, во-первых, точным заданием правил вывода, во-вторых, вместо содержательных рассуждений использует язык символов и формул, в результате чего содержательные рассуждения сводятся к преобразованию одних формул в другие, т. е. к особого рода исчислениям. В соответствии с этим одни и те же аксиомы могут описывать свойства и отношения различных по своему конкретному содержанию объектов.

Эта фундаментальная идея лежит в основе понятия абстрактной структуры. Н.Бурбаки выделяют три основных типа структур, которые играют важную роль при построении ими современной математики.

Алгебраические структуры.Примерами таких структур являются группы, кольца и поля. Основные характеристики алгебраической структуры: задание на некотором множестве А конечного числа операций с соответствующими свойствами, описываемых системой аксиом. В качестве элементов множества А могут выступать как математические объекты (числа, матрицы, перемещения, векторы), так и нематематические.

Структуры порядкахарактеризуются тем, что на рассматриваемом множестве задается отношение порядка (сравнение на числовых множествах), для которого выполняются следующие свойства: рефлексивность, симметричность, транзитивность.

Кроме основных трех типов структур (порождающих), в математике приходится рассматривать сложные структуры, где порождающие структуры органически связываются с помощью объединяющей системы аксиом. Например, множество действительных чисел является сложной структурой, в которую одновременно входят три основные порождающие структуры.

Накопленный в XVII и XVIII вв. огромный фактический материал привел к необходимости углубленного логического анализа и объединения его с новых точек зрения. Связь математики с естествознанием приобретает все более сложные формы. Новые теории стали возникать не только в результате непосредственных запросов практики, естествознания и техники, но также из внутренних потребностей самой математики. Наиболее важные из них: развитие теории функций, теории групп, связанной с исследованием проблемы разрешимости алгебраических уравнений в радикалах, создание неевклидовых геометрий.

Вторая особенность этого периода развития математики связана со значительным расширением области ее приложений. Если до этого математика применялась в таких разделах физики, как механика и оптика, то теперь ее результаты находят приложение в электродинамике, теории магнетизма, термодинамике. Резко возросли потребности техники в математике: баллистика, машиностроение и др.

Это развило столь же стройную и богатую содержанием геометрию, как и геометрия Евклида, послужило толчком в изменении взглядов на математику. Сразу встал вопрос о необходимости обоснования новой геометрии, исследовании ее непротиворечивости (из данной системы аксиом нельзя получить двух взаимоисключающих выводов). В этой связи получает дальнейшее развитие аксиоматический метод: 1) решается проблема непротиворечивости, полноты и независимости системы аксиом; 2) появляется новый взгляд на аксиоматическую теорию как бессодержательную, формально-логическую систему. Решение этих проблем было предложено Д. Гильбертом.

Новый взгляд на аксиоматический метод в корне изменил прежние представления о геометрии как полуэмпирической науке. Из открытий неевклидовых геометрий и построения их интерпретаций следовало, что евклидова и неевклидовы геометрии не представляют непосредственное описание эмпирических свойств реального физического пространства, а являются абстрактными системами утверждений, истинность которых может быть проверена после соответствующей конкретной интерпретации.

Однако подход Н.Бурбаки встретил и негативное отношение, поскольку они не считали нужным выяснять отношение рассматриваемых структур к действительному миру. Не имея возможности описать различные оценки философов и математиков и позиции Н.Бурбаки, остановимся на точке зрения ведущих отечественных математиков – А.Колмогорова, А.Александрова, В.Гнеденко. Они считают, что во времена Энгельса математика изучала количественные отношения между величинами и пространственными формами. Теперь она поднялась до изучения абстрактных структур и категорий. Но на этом основании нельзя считать, что объект изучения математики стал иным, что вместо количественного аспекта действительного мира математика стала исследовать нечто принципиально иное, что современный этап ее развития не связан с предшествующими этапами.

Эту позицию разделяет и А.Александров: в математике рассматриваются не только формы и отношения, непосредственно абстрагированные из действительности, но и логически возможные, определяемые на основе уже известных форм и отношений. Б. Гнеденко обращает внимание на то, что, хотя любая ветвь современной математики действительно изучает математические структуры, данное Н.Бурбаки определение отнюдь не находится в антагонистических отношениях с определением Ф.Энгельса, а лишь с определенных позиций его дополняет.

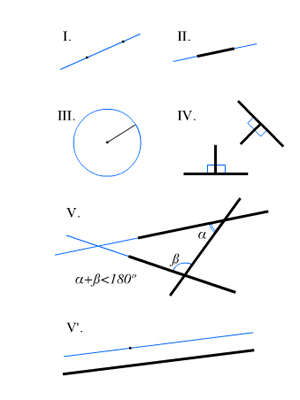
От всякой точки до всякой точки можно провести прямую.
Ограниченную прямую можно непрерывно продолжать по прямой.
Из всякого центра всяким раствором может быть описан круг.
Все прямые углы равны между собой.
Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых.

Тщательное изучение аксиоматики Евклида во второй половине XIX века показало её неполноту. В 1899 году Д. Гилберт предложил первую строгую аксиоматику евклидовой геометрии. Впоследствии еще не раз ученые предпринимали попытки усовершенствовать аксиоматику евклидовой геометрии. Кроме аксиоматики Гилберта, известными считаются: аксиоматики Тарского и аксиоматики Биргофа, которая состоит всего лишь из 4 аксиом.

В современной трактовке система аксиом Евклида может быть разделена на пять групп:

Аксиомы сочетания. Во-первых, через каждые две точки можно провести прямую и притом только одну. Во-вторых, на каждой прямой лежат по крайней мере две точки. При этом существуют хотя бы три точки, которые не лежат на одной прямой. В-третьих, через каждые три точки, не лежащие на одной прямой, можно провести плоскость и притом только одну. В-четвертых, на каждой плоскости есть по крайней мере три точки, а также существуют хотя бы четыре точки, не лежащие в одной плоскости. В-пятых, если две точки данной прямой лежат на данной плоскости, значит и сама прямая лежит на этой плоскости. В-шестых, если две плоскости имеют общую точку, то, следовательно они имеют и общую прямую.
Аксиомы порядка. Во-первых, если точка В лежит между А и С, то все три лежат на одной прямой. Во-вторых, для каждых точек А, В существует такая точка С, что В лежит между А и С. В-третьих, из трёх точек прямой только одна лежит между двумя другими. В-четвертых, если прямая пересекает одну сторону треугольника, значит она пересекает при этом и другую его сторону или проходит через вершину (отрезок AB определяется как множество точек, лежащих между А и В; аналогично определяются стороны треугольника).
Аксиомы движения. Во-первых, движение ставит в соответствие точкам точки, прямым прямые, плоскостям плоскости, сохраняя принадлежность точек прямым и плоскостям. Во-вторых, два последовательных движения вновь дают движение, и для всякого движения есть обратное. В-третьих, если даны точки А, A’ и полуплоскости A, A‘, ограниченные продолженными полупрямыми а, а’, которые исходят из точек А, A’, то существует единственное движение, переводящее А, а, A в A’, a’, A’ (полупрямая и полуплоскость легко определяются на основе понятий сочетания и порядка).
Аксиомы непрерывности. Во-первых, как гласит аксиома Архимеда, всякий отрезок можно перекрыть любым отрезком, откладывая на первом его достаточное количество раз (откладывание отрезка осуществляется движением). Во-вторых, согласно аксиоме Кантора: если дана последовательность отрезков, вложенных один в другой, то все они имеют хотя бы одну общую точку.
Аксиома параллельности Евклида: через точку А вне прямой а в плоскости, проходящей через А и а, можно провести лишь одну прямую, не пересекающую а.

Евклидова геометрия стала результатом систематизации и обобщения наглядных представлений человека об окружающем мире. Углубленное проникновение в суть геометрии привело к более абстрактному пониманию науки. Более поздние достижения и открытие показали, что наши представления о пространстве являются априорными, то есть чисто умозрительные. Таким образом было поставлено под сомнение существование единственной геометрии. бурное развитие физики и астрономии, доказало, что евклидова геометрия описывает структуру окружающего пространства, но вовсе не способна описать свойства пространства, связанные с перемещениями тел со скоростями, близкими к световой. Русский математик Н. И. Лобачевский разработал новую неевклидову геометрию, которая приблизилась к реальному описанию физического пространства.

Слайд 1

Слайд 2

Актуальность темы заключается в том, что знание основ евклидовой геометрии является в настоящее время необходимым элементом общего образования во всем мире. Актуальность темы заключается в том, что знание основ евклидовой геометрии является в настоящее время необходимым элементом общего образования во всем мире.

Слайд 4

Биография Евклида Евклид или Эвклид — древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике. Жил примерно в 300 г. до нашей эры.

Слайд 7

VI книга – прилагается к теории подобных фигур; VI книга – прилагается к теории подобных фигур; VII-IX книги – посвящены теории чисел; X книга – строится классификация иррациональностей; XI книга – содержит основы стереометрии; XII книга – доказываются теоремы об отношениях площадей кругов, объёмов пирамид и конусов; XIII книга – посвящена построению пяти правильных многогранников.

Слайд 8

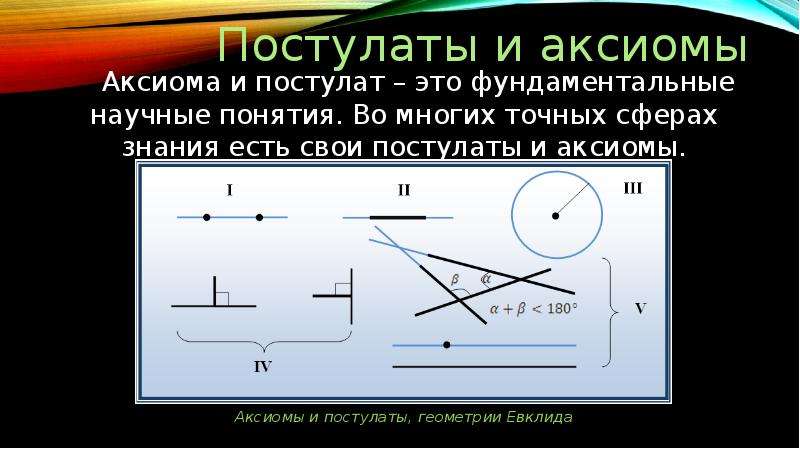
Постулаты и аксиомы Аксиома и постулат – это фундаментальные научные понятия. Во многих точных сферах знания есть свои постулаты и аксиомы.

Слайд 9

Слайд 10

Евклид и античная философия Со времён пифагорейцев и Платона геометрия, арифметика и другие математические науки рассматривались в качестве -образца систематического мышления -предварительной ступени для изучения философии.

Слайд 12

Выводы: Выводы: 1. Евклид или Эвклид — древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике. Жил примерно в 300 г. до нашей эры.

Слайд 14

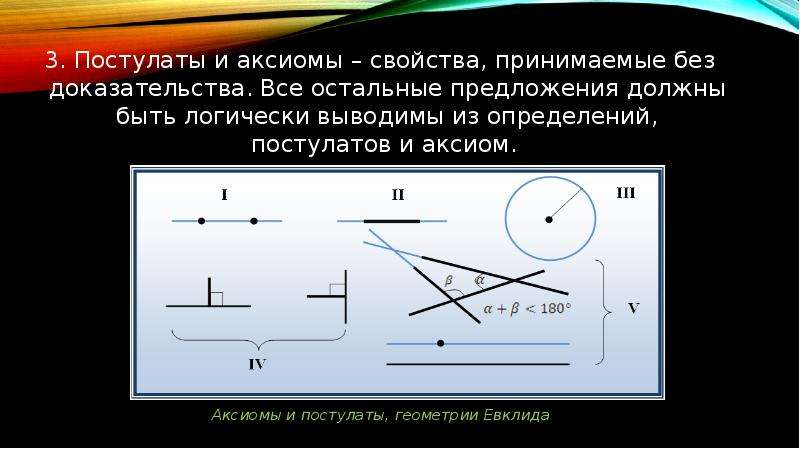
3. Постулаты и аксиомы – свойства, принимаемые без доказательства. Все остальные предложения должны быть логически выводимы из определений, постулатов и аксиом. 3. Постулаты и аксиомы – свойства, принимаемые без доказательства. Все остальные предложения должны быть логически выводимы из определений, постулатов и аксиом.

Слайд 15

4.В целом, выбор постулатов и аксиом у Евклида удачен, но его система не является полной: в ней отсутствуют многие важные аксиомы (например, стереометрические). Впрочем, еще Аристотель полагал, что иногда изложения той или иной науки обходят молчанием некоторые свойства и положения вследствие их очевидности. Вполне возможно, что Евклид не ставил себе целью дать полный список утверждений, необходимых для дальнейших доказательств. 4.В целом, выбор постулатов и аксиом у Евклида удачен, но его система не является полной: в ней отсутствуют многие важные аксиомы (например, стереометрические). Впрочем, еще Аристотель полагал, что иногда изложения той или иной науки обходят молчанием некоторые свойства и положения вследствие их очевидности. Вполне возможно, что Евклид не ставил себе целью дать полный список утверждений, необходимых для дальнейших доказательств.

Слайд 16

5. Со времён пифагорейцев и Платона геометрия, арифметика и другие математические науки рассматривались в качестве 5. Со времён пифагорейцев и Платона геометрия, арифметика и другие математические науки рассматривались в качестве -образца систематического мышления -предварительной ступени для изучения философии.

Слайд 18

Заключение Значение геометрии огромно. Все, что нас окружает, имеет геометрическую форму. Геометрия встречается во многих профессиях, без которых человечество не смогло обойтись. Можно сделать вывод, что если бы люди не начали изучать геометрию, то прогресс и множество современных изобретений дались бы человечеству с большим трудом и возможно гораздо позже.

Слайд 19

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

МИНОБР НАУКИ РОССИИ

Федеральное государственное автономное образовательное

учреждение высшего образования

Институт математики, механики и компьютерных наук

им. И.И. Воровича

Кафедра теории и методики математического образования

Гречкина Ольга Сергеевна

по истории математики

Научный руководитель –

к.п.н., доц. – Пырков Вячеслав Евгеньевич

Ростов-на-Дону

Список использованной литературы…………………………………….. 17

Биография Евклида

1. Евклид

Талантливый математик Древней Греции Евклид (Euclid) предположительно родился в 331 году до н.э. в зажиточной семье из Тира. Обучался в платной школе-академии Платона в окраинном публичном саду Афин таким дисциплинам как: математика, естествознания, диалектика, философия и другие.

Евклид с первых уроков влюбился в математику, хотя ему нравилось философствовать в кругу таких же учеников как он, особенно на свежем воздухе в период симпозиумов-застолий поедая зеленые оливки, засушенные фиги и запивая красным вином.

После окончания школы Евклид переезжает в Александрию, один из крупнейших центров Западного мира, вдобавок ко всему, еще здесь производился папирус. Правитель Египта Птоломей I был мудрым и щедрым, в столицу египетского государства съезжались со всего света по его личному приглашению поэты и музыканты, философы и ученые. Специально для них был построен Храм Муз, астрономическая вежа, многочисленные обособленные комнаты для работы, потрясающая библиотека с огромным фондом редких книг. Открылся ботанический сад.

Благодаря приобретенному опыту в школе Платона Евклид прививал любовь к знаниям своим ученикам, помогал им разобраться в написании их собственных трудов и теорий, вел продолжительные философские беседы, всячески заботился о них и проявлял интерес к их дальнейшей судьбе. Евклид трепетно относился к музыке, имел хороший музыкальный слух, изобрел монохорд. И собственно, благодаря его усилиям использование трех струн стало нормой. Совершенно неожиданным образом стал прародителем, заложившим основу изобретению клавишных инструментов: от клавесина с щипковым звукоизвлечением до пианино с молоточковым способом извлечения звуков.

И что вполне естественно, первопричиной появления инструментов стала наука о числах. Умер отец геометрии Евклид предположительно в 272 году до н. э. в Александрии, оставив после смерти богатое наследие. Его книги продавались огромными тиражами и являлись информационным родником вдохновения для многих ученых всего мира.

1 . Птолемей и Евклид

Несколько любопытных фактов из биографии Евклида:

Самый древний известный математический трактат принадлежит Евклиду.

До сих пор нет данных о месте рождения и смерти великого ученого. Однако известно место занятий Евклида примерно 2400 лет назад и место его нахождения — Александрия. Интересно, что этот городок сегодня — второй по размерам в Египте после Каира.

Евклид смог создать 4 книжки по коническому виду сечений.

С самой юности Евклид обучался у именитого ученого Платона, обучавшего Аристотеля в Древней Греции. Сам же Платон обучался у Сократа.

По традиции геометрия сегодня носит название этого ученого.

Есть легенда, что когда один раз ученик величайшего математика спросил у него, как геометрия может помочь ему в жизни, то Евклид дал ему денег и прогнал с занятий.

Евклид до сих пор считается автором многочисленных книг, чье авторство не было подтверждено. Это разные труды, к примеру, публикации по музыке, философии и медицине. Официально известно, что великий ученый сделал открытие в оптических и астрономических областях.

Сегодня признают римановскую, лобачевскую и евклидову геометрию. Последняя — самая традиционная и часто используемая.

В целом, Евклид является отцом геометрии, и он не случайно так

называется. Он первым сделал сложное понятным и дал толчок развитию естественных наук. Его книги неоценимы по значимости и применяются сегодня в области математических и геометрических наук во всем мире.

Читайте также: