Движение частиц в поле прямоугольной ступеньки доклад

Обновлено: 26.07.2024

Рассмотрим движение частицы в силовом поле, в котором потенциальная энергия изменяется с координатой так, как показано на рис.2. Частица, имеющая полную энергию, движется вдоль оси. В левой части рисунка потенциальная энергия равна нулю, а в правой

части – постоянное значение.

Точка - точка поворота, где кинетическая энергия равна нулю. Классическая частица, достигнув

этой точки, остановится и начнет двигаться

в обратном направлении. Область для неё

Решением уравнения Шредингера

должна быть непрерывная функция ,имеющая

непрерывную первую производную. При значении

разности производная,

и волновая функцияне может сразу

обратиться в нуль справа от . В соответствии

с вероятностным смыслом волновой функции

это означает отличную от нуля вероятность обнаружить частицу в области .

Квантовая частица способна проникать в область, запрещенную классической механикой.

Чтобы упростить ситуацию, заменим непрерывную функцию , изображенную на рис.2,, ступенчатой функцией, показанной на рис.2,б, а начало координат поместим в точку поворота, так что . Будем искать решение уравнения Шредингера в областях 1 и 2.

В области 1, (), уравнение Шредингера принимает вид, где, два штриха над волновой функцией означают двойную производную по. Общее решение этого уравнения

Представляет сумму двух волн, падающую с амплитудой А и отраженную от потенциальной ступеньки волну с амплитудой В.

В области 2, (), уравнение Шредингера, где, имеет общее решение

. Поскольку должна быть ограниченной, а второе слагаемое в решении неограниченно возрастает с увеличением, то необходимо, чтобы. Таким образом физически приемлемым решением является

На границе раздела областей 1 и 2, то есть при x = 0, должны выполняться условия непрерывности пси-функций и их производных:

, или(8)

, или

Граничные условия (8) позволяют выразить коэффициенты В и С через амплитуду А падающей волны. В результате находим

₍₉₎

_{На рис.3 представлена зависимость плотности вероятности обнаружения частицы от координаты} _x_.

Коэффициент отражения определяет вероятность того, что частица отразится от ступеньки.

То, что , означает: в установившемся (стационарном) состоянии вся энергия падающей волны отражается, однако в классически запрещенной областисуществует определенная вероятность обнаружить там частицу. И эта вероятность равна

. (10)

плотность вероятности уменьшается враза. Величинаназываетсяэффективной глубиной проникновения квантовой частицы в область, запрещенную классической механикой.

Прохождение частицы массы m над барьером, когда (рис.4).

С точки зрения классической механики ни одна частица в этом случае не будет отражаться от скачка потенциальной энергии в точке x = 0/

Решение уравнения Шредингера аналогично предыдущему случаю, и мы получаем

: ,

Из граничных условий о непрерывности функций и их производных принаходим

амплитуды B и C:

, (11)

По аналогии с плотностью потока частиц , гдескорость частиц,плотность

частиц (число частиц в единице объема), введем плотность потока вероятности

где скорость одной частицы.

Определим коэффициенты отражения и прохождения:

(12)

(13)

В (13) использовалось соотношение . Можно убедиться, что.

Таким образом, существует отличная от нуля вероятность отражения, даже если .

Этот эффект является чисто квантовым и объясняется наличием у частицы волновых свойств.

Интересно отметить, что коэффициенты ине изменятся, еслиипоменять местами, что соответствует случаю, когда частица движется к потенциальной ступеньке справа налево.

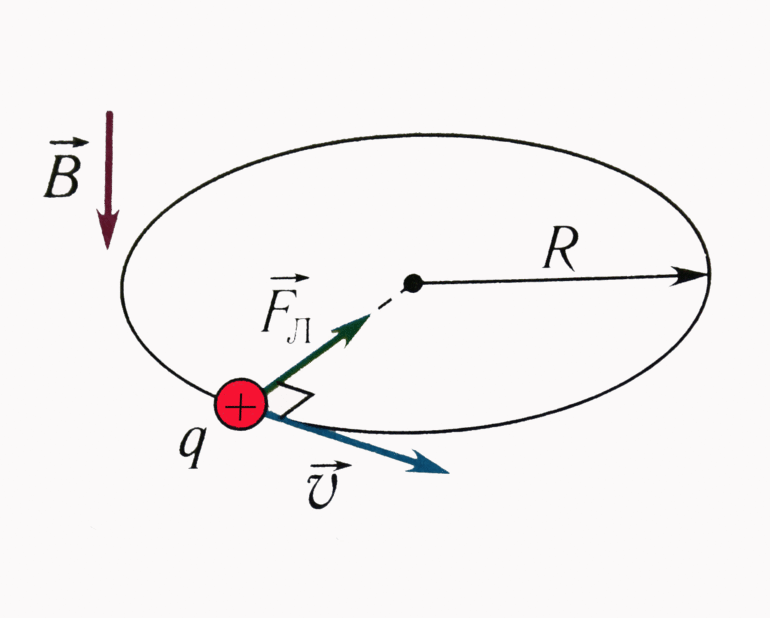
Сила Лоренца направлена по правилу левой руки: если пальцы указывают направление вектора скорости частицы, а линии магнитной индукции “втыкаются” в ладонь, то большой палец укажет направление действия силы (для положительно заряженных частиц). То есть в любой момент времени сила направлена перпендикулярно скорости, а это значит, что двигаться частица будет по окружности.

Задача 1. Электрон движется в однородном магнитном поле с индукцией Тл перпендикулярно линиям поля. Определить силу, действующую на электрон со стороны поля, если радиус кривизны траектории см.

Сила Лоренца направлена все время перпендикулярно скорости, и поэтому траектория частицы закручивается. По второму закону Ньютона

$a=\frac<\upsilon^2> $

$q B=\frac<m\upsilon> $

$\upsilon=\frac<qBR> $

$F=\frac<q^2B^2R> =\frac\cdot10^\cdot0,005>>=0,14\cdot10^$

Ответ: 1,4 пН
Задача 2. Определить частоту обращения электрона по круговой орбите в магнитном поле, индукция которого Тл.
По второму закону Ньютона

$a=\frac<\upsilon^2> $

$q B=\frac<m\upsilon> $

$\frac<\upsilon> =\frac< q B >$

$\nu=\frac<1> =\frac<\upsilon><2\pi R>=\frac< q B >=\frac\cdot0,2>>=5,6\cdot10^9$

Ответ: Гц, или 5,6 ГГц.
Задача 3. Электрон влетает в однородное магнитное поле перпендикулярно силовым линиям. Скорость электрона м/с, индукция магнитного поля мТл. Определить нормальное, тангенциальное ускорение электрона и радиус кривизны его траектории.

$q B=\frac<m\upsilon> $

$R=\frac< m\upsilon > =\frac< 9,1\cdot10^\cdot4\cdot 10^7>\cdot10^>=2,275\cdot10^$

Тогда нормальное ускорение равно:

$a_n=\frac<\upsilon^2> =\frac=7\cdot10^$

$a_<\tau> =0$

Ответ: мм, " width="96" height="18" />
м/с , =0" width="50" height="15" />
.

Задача 4. Частица массой влетает перпендикулярно силовым линиям в однородное магнитное поле с индукцией В. Заряд частицы . Доказать, что период обращения частицы не зависит от ее скорости.

По второму закону Ньютона

$a=\frac<\upsilon^2> $

$q B=\frac<m\upsilon> $

$\upsilon=\frac< q B R> $

$T=\frac<2 \pi R> Период обращения – время одного оборота. Пусть частица движется по окружности радиуса , тогда длина этой окружности . Период будет равен <\upsilon>$
, а скорость частицы мы нашли, поэтому

$T=\frac<2\pi R m> < q B R >=\frac< 2 \pi m >< q B >$

$T=\frac< 2 \pi m > Ответ: < q B >$
– не зависит от скорости.

Задача 5. Электрон движется в однородном магнитном поле с индукцией Тл по окружности радиусом см. Определить импульс электрона.

По второму закону Ньютона

$a=\frac<\upsilon^2> $

$q B=\frac<m\upsilon> $

$\upsilon=\frac< q B R> $

Импульс электрона будет равен

$p=m\upsilon= q B R=0,015\cdot0,1\cdot 1,6\cdot10^<-19> =2,4\cdot 10^$

$p=2,4\cdot 10^<-22> Ответ:$
кг м/с.

Задача 6. Электрон движется в магнитном поле с индукцией Тл по окружности радиусом см. Определить кинетическую энергию электрона (в джоулях и электрон-вольтах).

По второму закону Ньютона

$a=\frac<\upsilon^2> $

$q B=\frac<m\upsilon> $

$\upsilon=\frac< q B R> $

$E_k=\frac<m\upsilon^2> =\frac< q^2 B^2 R^2>=\frac\cdot0,02^2\cdot0,01>>=5,6\cdot10^$

Или в электронвольтах эВ.

$E_k=5,6\cdot10^<-16> Ответ:$
или 3500 эВ.
Задача 7. Заряженная частица с кинетической энергией Ек = 1 кэВ движется в однородном магнитном поле по окружности радиусом мм. Найти силу, действующую на частицу со стороны поля. 13.68.

По второму закону Ньютона

$F=ma=\frac<m\upsilon^2> =\frac=\frac>>=3,2\cdot10^$

$F=3,2\cdot10^<-13> Ответ:$
Н.

В физике электрическое поле принято описывать величиной, характеризующей действие на единичный электрический заряд. В электродинамике воздействие, которое приводит в движение частицы в магнитном поле, называют силой Лоренца.

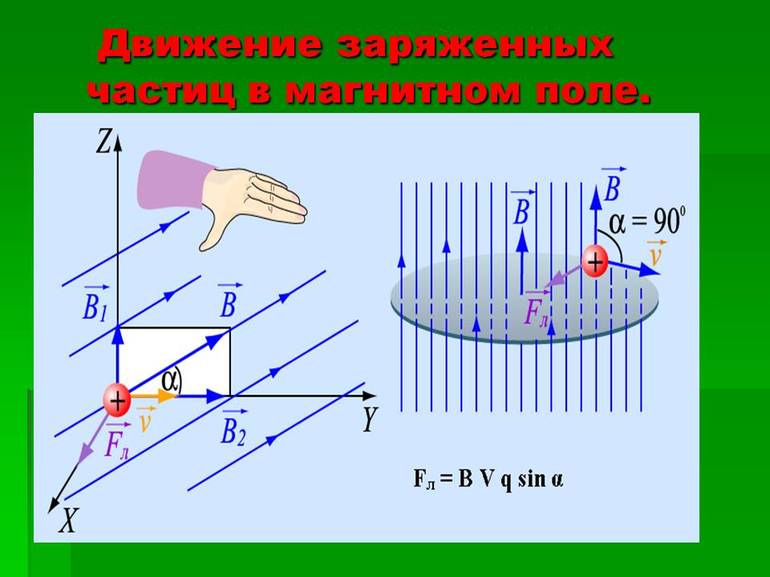
Её главная особенность — для неё не выполняется третье утверждение Ньютона, но справедливо правило сохранения импульса. При этом макроскопическим проявлением перемещения является закон взаимодействия токов.

Общие сведения

Ещё в III—II тысячелетии на острове Магнезия были обнаружены камни, обладающие странными свойствами. Они имели способность притягивать к себе железные предметы. Эти вещества в честь острова получили название магниты. Так как их свойства сохраняются в течение длительного времени, их считают постоянными. Было установлено, что если такой камень разместить на поплавке и положить на него магнит, при его развороте он вернётся в начальное положение. Другими словами, он всегда стремится ориентироваться определённым образом.

Если взять 2 магнита, то, в зависимости от их расположения, они могут притягиваться друг к другу или отталкиваться. Этот эффект объясняется наличием у намагниченных веществ двух полюсов. В 1820 году Христиан Эрстед читал лекцию о тепловом действии тока. Он через проволоку пропускал электричество, демонстрируя, как она разогревается.

Во время эксперимента один из студентов обнаружил, что когда замыкалась цепь, стрелка у рядом находящегося компаса отклонялась. Это вращение и позволило обнаружить связь между электричеством и магнетизмом.

Учёный начал экспериментально изучать эффект. Он предположил, что, так как электрический ток — направленное движение в проводнике заряженных частиц, существует какая-то сила, возникающая вокруг проводящего тела. Обнаружить её можно с помощью компаса. Эту особую пространственную материю назвали магнитным полем. Воображаемые направления, вдоль которых бы расположились стрелки компасов, назвали силовыми линиями.

Опытным путём были установлены характеристики, описывающие движение заряженной частицы в магнитном поле.

К основным из них относят:

Индукцию. Это плотность магнитных линий. С их помощью вещества разделяют на однородные и неоднородные. В первых магнитная индукция в каждой точке материи имеет одинаковое значение. Определяют её как отношение потока к площади поперечного сечения проводника.
Проницаемость. Описывает способность среды создавать магнитные силы. Величиной, характеризующей это свойство, является абсолютное значение.
Напряжённость. Изменяется в зависимости от силы тока в проводнике и его формы.

Описать магнитную материю можно численно и направлением. За её ориентацию принимается северная сторона, на которую указывает стрелка компаса.

Либо за неё можно принять расположение положительной нормали с током в рамке. Определяют её по правилу буравчика.

Рамка с током

Физиками было установлено, что если взять рамку и пропустить по ней ток, магнитное поле окажет влияние на электроны. В результате происходит их обращение. Вращательное действие силы характеризуется моментом энергии. Именно он и описывает действие материи.

Пусть в магнитном поле расположена прямоугольная рамка. По ней циркулирует ток против часовой стрелки. Вектор индукции направлен вверх. За направление магнитных линий принимается положительная нормаль. По правилу буравчика, если направление поступательного движения винта будет совпадать с направлением тока в проводнике, то вращение винта укажет расположение вектора магнитной индукции поля, создаваемого движением частиц.

Угол между нормалью и вектором обозначают буквой альфа. Естественно, что рамка стремится развернуться так, чтобы быть перпендикулярно полю. Но если она не совпадает с ним по направлению, на неё действует момент силы. Чтобы провести расчёты, необходимо выбрать ось относительно рамки.

Пусть она будет проходить параллельно длинным линиям прямоугольника. Для удобства длина её будет равняться a, а ширина b.

На такую установку будет действовать сила Ампера. Её определение звучит так: модуль вектора равен произведению магнитной индукции на силу тока в проводнике, его длине и синусу угла между направлением поля и заряженными частицами: F = B * I * L * sin (j). Она действует на все стороны рамки. При этом отличается только по направлению.

На рамку оказываются следующие воздействия:

На дальнюю длинную сторону действует сила равная F1. Значит, на параллельную ей боковую грань воздействие будет противоположно по направлению -F2, поэтому силы принимаются по модулю. Так как значение тока везде одинаковое, можно записать: F = |F1| = |F2|.
На короткие грани действуют силы, перпендикулярные проводнику. Они будут не поворачивать, а растягивать рамку. Соответственно, их можно обозначить как F3 и F4.

F1 и F2 создают нулевой момент. Они параллельны и направлены в противоположную сторону, образуют пару силы действующих в магнитном поле. Вычисляется она по формуле: M = F * d, где d — расстояние между воздействующими линиями энергии. Таким образом, момент силы в рамке будет определяться так: M = B * a * b * sin (j).

Если принять, что на прямоугольнике намотан провод с числом витков n, а произведение a * b — это площадь, формула примет окончательный вид: M = B * S * n * sin (j).

Сила Лоренца

Магнитное поле действует только на ту частицу, что подвергается воздействию силы Ампера. Пока электрон будет двигаться хаотично, никакого магнитного поля вокруг него не возникнет. Причём эта сила перпендикулярна проводнику и полю.

Получается, что причиной возникновения силы Ампера является какая-то материя, действующая на траекторию заряженных частиц, когда они начинают двигаться в поле.

Пусть в проводнике есть носители зарядов. Их массой в этом случае можно пренебречь. Так как частицами являются отрицательно заряженные электроны, движутся они противоположно направлению тока. На каждый заряд действует сила, которая в сумме даст силу Ампера.

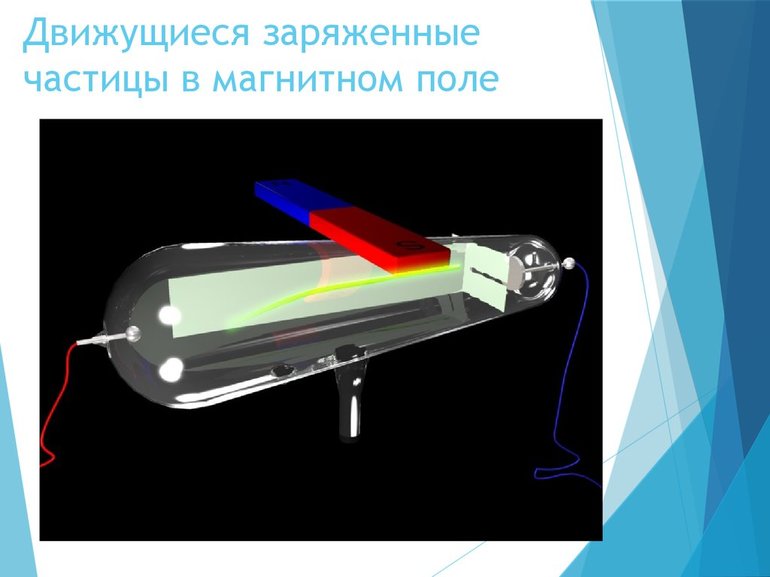
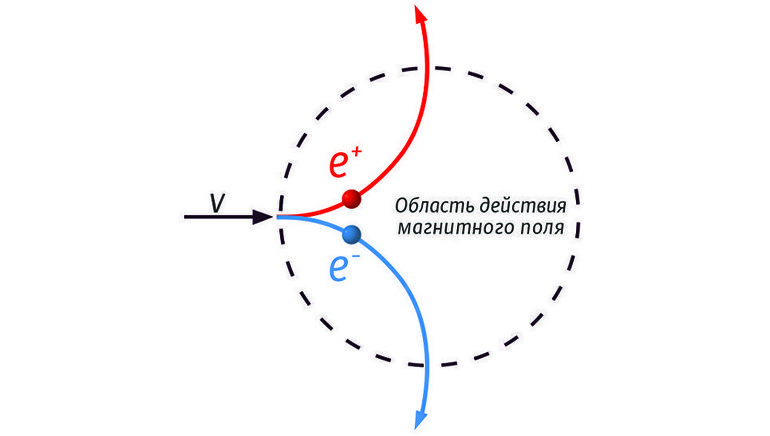
Если взять воображаемое увеличительное стекло и посмотреть, что происходит в середине проводника, возможно было бы увидеть следующее: в окружности тела электрон перемещался бы встречно току и испытывал действие силы, перпендикулярной его движению. Именно она и называется силой Лоренца. Кратко её определение звучит так: равнодействующая всех энергий Ампера, действующих на заряженные частицы, которые перемещаются в поле. Обозначают её Fл.

Кинетическая сила возникает только при движении. Если частица нейтральная (нейтрон), воздействие на неё не оказывается. Чтобы рассчитать эту силу, нужно знать длину проводника и скорость перемещения носителей заряда. Время, которое потребуется электрону, чтобы сменить своё положение, определяют из равенства: t = L / V.

Всю совокупность прошедших частиц можно обозначить Qоб. Это общий заряд, прошедший через радиус проводника за t. Он будет равняться: Qоб = I * t = (I * L) / V.

Учитывая определение, можно утверждать, что Fa = Fл * N. Так как количество частиц, находящихся в проводнике, равняется всему заряду в нём N = Qоб / Q, можно записать: N = I * L / V * Q. Отсюда сила Ампера: Fa = Fл * (I * L) / (V * q). Если сделать подстановку Fа и выразить силу Лоренца, формула для её определения примет вид: Fл = Q * V * B * sin (j), то есть она пропорциональна скорости частицы в магнитном поле, вектору направления индукции и количеству зарядов. Причём сила Лоренца будет наибольшей, когда V перпендикулярно B.

Решение задач

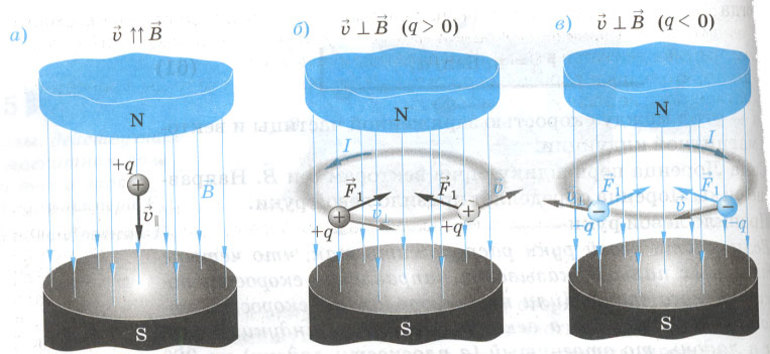
Исследования движения частиц в поле, вызванном магнитной энергией заключается в нахождении сил Лоренца и Ампера за период протекания электрического тока. Существуют определённые типы заданий, с помощью которых можно лучше понять изученный материал и наглядно увидеть, как тесно геометрия переплетается с физикой. Вот некоторые из них:

Плоская прямоугольная катушка со сторонами 10 и 5 см, состоящая из 200 витков, находится в однородном поле с индукцией 0,05 Тл. Какой максимальный винтовой момент может действовать на катушку, если сила тока 2 А. Для решения этой задачи нужно использовать формулу: M = n * B * I * S * sin (j). Наибольший момент будет, когда синус альфа равняется 1. Значит: M = n * B * I * a * b = 200 * 0,05 H / A* m *2 А * 0,1 м = 0, 1 Н * м. Задача решена.

Квадратная рамка с током закреплена так, что может свободно вращаться вокруг горизонтально расположенной стороны. Находится она в вертикальном однородном поле индукции B, массой m, а угол наклона к горизонту j. Найти силу тока в рамке. В устройстве циркулирует ток. Значит, существует момент силы. Условие механического равновесия будет выполнено когда: Mmg + Mмаг = 0. Учитывая, что Mmg = mg * d, а d = q * cos (j) / 2 можно записать: Mmg = mg * а q / 2, а Mмаг = - B * I * S * sin (j). На этом шаге можно найти знак по правилу буравчика. Значит: B * I * a 2 * sin (j) = (mg * a cos (j)) /2. Отсюда: I = (mg) / (2 * B * a * tg (j)).

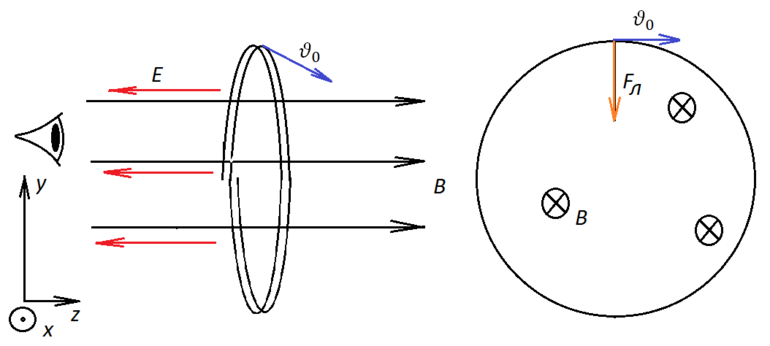
Индукция уловителя пылинок на базе масс-спектрометра имеет значение 0,1 Тл. Напряжение создаёт поле 10 кВ. В устройстве ионы попадают на пластинку, являющуюся датчиком загрязнения. Найти, на каком расстоянии от щели будут полосы ионов 2 H + .

Заряды двигаются по окружности. Согласно второму закону Ньютона: Fл = mg = q * V * B. Центростремительное ускорение: a = V2/ r. Отсюда: r = mV / qB. Пролёт ионов занимает половину радиуса. С учётом равенства mV 2 / 2 = q * U, рабочая формула примет вид: X = (2/ B) * √(2mV / q) = 2 А*м / 0,1 Н * √ (2 * 1,67 * 10 -27 кг * 10 4 В / 1,6 + 10 -19 Кл) = 0,289 м.

Часто решение задач требует не только знания нескольких формул, но и понимания, на какую частицу действует магнитное поле и какие силы при этом возникают. Кроме этого, приходится условие изображать схематично на рисунке.

Это часто необходимо для правильного определения направлений действующих сил и упрощения понимания задания. Не стоит забывать, что все вычисления выполняются в системе СИ.

Знакомство с современной физикой, в отличие от физики классической, вызывает естественные трудности восприятия основных понятий и идей квантовой механики - этого совершенно нового способа описания состояния микрочастиц и динамических законов, управляющих их движением.

Законы квантовой механики составляют основную теоретическую базу в изучении строения вещества. Так, опираясь на них, удалось выяснить строение атомов, установить природу химической связи, объяснить периодическую систему элементов, понять строение атомных ядер и свойства элементарных частиц.

Трудности при знакомстве с основами квантовой механики начинаются уже с описания основных характеристик самой микрочастицы, ее физического состояния, и, вообще, возможности задания ее начального и текущего состояния и контроля изменения этого состояния в процессе взаимодействия частицы с окружающими ее телами.

Даже сама возможность использования таких, казалось бы очевидных понятий, как пространственное положение микрочастицы, его изменение во времени, движение по траектории - для микрочастицы становится проблематичной. Более того, возникает существенное, неожиданное осложнение, связанное с взаимодействием микрочастицы с контролирующим ее движение измерительным прибором. Если в классической физике молчаливо предполагалось, что этим влиянием можно пренебречь, то в квантовой механике, как оказалось, воздействие прибора на микрообъект может радикально изменить его состояние.

Поэтому в теоретическую ткань квантовой механики органично вплетена взаимосвязь величин, характеризующих сами микрочастицы, с физическими величинами, непосредственно измеряемыми приборами.

Настоящая работа, позволит студенту более наглядно познакомиться с удивительными свойствами микрочастиц при их движении и взаимодействии с силовыми физическими полями в самых простых модельных ситуациях.

В процессе подготовки к выполнению работы и при ее непосредственном выполнении студенты приобретают необходимые первоначальные навыки и представления об основных понятиях и этапах решения типичной квантово-механической задачи.

На примере простейших барьерных задач в работе проводится компьютерное моделирование поведения микрочастицы в силовых полях с прямоугольным потенциалом (типа потенциальной ступени или барьера.)

С этой целью вначале студенту предлагается просмотреть демонстрационную программу, в которой моделируется поведение микрочастицы в зависимости от ее массы и энергии и от изменения силового поля, действующего на микрочастицу.

Можно наблюдать, как при варьировании энергии и массы закономерно меняются амплитуды отраженной и проходящей волн и, что особенно важно, наблюдать типичный квантово - механический эффект - эволюцию осциллирующих функций в экспоненциальные волновые, что соответствует некоторой глубине проникновения Xmax частицы в классически недоступную область.

Прочувствовав механизм возникновения туннельного эффекта, далее, в основной программе, студент уже самостоятельно на примере конкретного задания анализирует изменение состояния частицы и ее движение в двух вариантах силовых полей:

- Потенциальный скачок (ступенька)

В конце работы студент должен графически проанализировать изменение коэффициентов отражения (R) и прохождения (Т), а для случая потенциального барьера, кроме того, провести графический анализ вероятности просачивания сквозь него (D₁) в зависимости от ширины барьера - L, массы частицы - mas и энергии частицы (U₀-E).

1 Основные положения, касающиеся движения микрочастиц в потенциальных полях

1.1 Квантово-механическое описание движения частиц в одномерном случае

Рассмотрим одномерный случай.

Тогда динамическое уравнение, решения которого определяют движение микрочастицы, запишется:

(x,t) - волновая функция, описывающая состояние микрочастицы;

h - постоянная Планка;

U(x,t) - потенциал силового поля, действующего на частицу.

В алгебре решением уравнения называют числа - корни уравнения, которые будучи подставленными в уравнение, обращают его в тождество. Решением дифференциального уравнения называют функцию, которая будучи подставленной в уравнение со всеми своими производными, также обращает его в тождество.

В случае постоянства потенциала решение уравнения (1) имеет вид волн де-Бройля.

где импульс частицы:

А и В произвольные постоянные, которые ищутся из граничных условий. В решении (2) первое слагаемое представляет собой волну, распространяющуюся вправо, а второе - волну, бегущую влево.

Далее рассмотрим два типичных случая движения микрочастицы в поле прямоугольного потенциала.

1.1.2 Потенциальный скачок

Низкий потенциальный скачок ( см. Рисунок 1).

В этом случае энергия частицы больше высоты потенциального скачка (E>U).

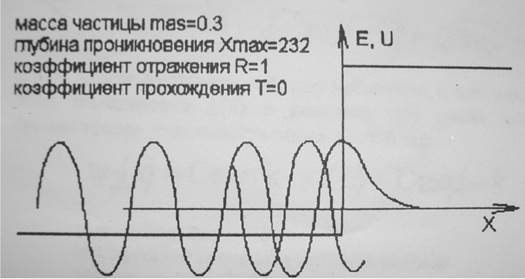
Рисунок1 - Решение уравнения Шредингера для случая высокой потенциальной ступеньки

Для стационарного случая (независимости физической ситуации от времени) решение уравнения Шредингера

в соответствии с выражением (2) будет представлено для области слева от х=0 суммой падающей волны и отраженной:

Здесь в отсутствие силового поля в первой области (U=0) согласно (3)

В области справа от x=0 решение будет представлено амплитудой прошедшей волны:

(6a)

Для того, чтобы задача имела конкретно завершенный вид и имела четкий физический смысл, необходимо в решениях (5-6) найти неопределенные коэффициенты А, В и С. Для нахождения этих коэффициентов используют аксиоматические свойства волновой функции (x):

Читайте также: