Доклад уравнение гармонической волны

Обновлено: 02.07.2024

Изменения состояния среды, распространяющиеся в этой среде и несущие с собой энергию, называются волнами.[1]
Для волн любой природы характерно распространение с конечной скоростью и перенос энергии без переноса вещества.
Волны могут иметь различную форму. Различают одиночные волны или импульсы – сравнительно короткие возмущения; цуги волн – ограниченный ряд повторяющихся возмущений (например, отрезок синусоиды); гармонические волны (бесконечно синусоидальные волны).
Задачи распространения гармонических волн относятся к задачам стационарной динамики.

Содержание

. Гармонические волны: основные понятия и определения. 3
2. Постановка задачи. 8
3. Исследование модельных задач. 12
3.1. Частоты толщиных резонансов. 12
3.2. Дисперсионные уравнения Рэлея-Лэмба. 16
3.3. Асимпттотики дисперсионного уравнения Релея-Лэмба. 21
4. Список использованных источников и литературы. 25

Прикрепленные файлы: 1 файл

КУРСОВАЯ з.doc

1. Гармонические волны: основные понятия и определения. 3

2. Постановка задачи. . . . 8

3. Исследование модельных задач. . . 12

3.1. Частоты толщиных резонансов. . . 12

3.2. Дисперсионные уравнения Рэлея- Лэмба. . 16

3.3. Асимпттотики дисперсионного уравнения Релея-Лэмба. 21

4. Список использованных источников и литературы. . 25

1. Гармонические волны: основные понятия и определения

Изменения состояния среды, распространяющиеся в этой среде и несущие с собой энергию, называются волнами.[1]

Для волн любой природы характерно распространение с конечной скоростью и перенос энергии без переноса вещества.

В [2] приведён следующий критерий: если характерный размер системы (где - скорость распространения возмущения, - время заметного изменения этого возмущения), о процессе следует говорить как о колебательном, происходящем в системе с сосредоточенными параметрами; если , то систему следует считать распределённой, а происходящий в ней процесс – волновым.

Волны могут иметь различную форму. Различают одиночные волны или импульсы – сравнительно короткие возмущения; цуги волн – ограниченный ряд повторяющихся возмущений (например, отрезок синусоиды); гармонические волны (бесконечно синусоидальные волны).

Задачи распространения гармонических волн относятся к задачам стационарной динамики. В задачах нестационарной динамики закон изменения искомых величин по времени неизвестен и требует определения. В задачах стационарной динамики предполагается, что все величины изменяются по времени по гармоническому закону:

где круговая частота, ;

- переменная фаза колебаний;

Наряду с (1.1), (1.2) используются комплексные представления:

где - комплексная амплитуда;

В задачах стационарной динамики начальные условия не ставятся. определена с точностью до произвольной постоянной : . Обычно полагают .

Если требуется, чтобы решение в виде (1.1) удовлетворяло всем граничным условиям на поверхности ограниченного тела, то говорят, что изучаются установившиеся колебания тела.

Если рассматривается бесконечное тело, то говорят, что изучается распространение гармонических волн.

Гармоническая волна является идеализированной, её возбуждение в реальных условиях проблематично. Однако, её важное значение заключается в том, что волну любой формы можно представить как сумму гармонических волн различных частот (гармоник). В линейных распределённых системах выполняется принцип суперпозиции, приводящий к тому, что эффекты, вызываемые негармоническими волнами, могут быть определены как сумма эффектов, создаваемых в отдельности каждой из её гармонических составляющих.

Если является линейной функцией , то говорят, что в теле распространяется плоская волна.

Если имеет вид , то говорят, что плоская волна распространяется в направлении оси .

Пусть тело представляет собой волновод, например, представляет собой цилиндр с направляющей параллельной оси или слой конечной толщины. В этом случае ищется решение вида:

и требуется, чтобы оно удовлетворяло граничным условиям на боковой поверхности волновода. В комплексной форме плоская волна, распространяющаяся в направлении оси имеет вид:

Модами называют частные решения, или волны, распространяющиеся вдоль оси волновода и удовлетворяющие граничным условиям на боковой поверхности волновода. Так же их называют нормальными волнами.

Запишем уравнение движения постоянной фазы:

Поверхность постоянной фазы представляет собой плоскость, перпендикулярную оси . Эта плоскость перемещается параллельно самой себе со скоростью

называемой фазовой скоростью. Таким образом, фазовая скорость – это скорость движения поверхности постоянной фазы.

Путь, проходимый поверхностью постоянной фазы за время равному периоду колебаний , называется длиной волны.

Решение в виде (1.4) должно удовлетворять граничным условиям на боковой поверхности. Из-за этого величины и не являются независимыми: . Тогда фазовая скорость также является зависимой от волнового числа:

Явление зависимости фазовой скорости гармонической волны от волнового числа или частоты называется дисперсией. Дисперсия может быть вызвана не только наличием границ, но и физическими свойствами среды (в идеально упругом теле этот вид дисперсии отсутствует).

Соотношение, связывающее и , называется дисперсионным уравнением. В общем виде записывают следующим образом:

Если фазовая скорость является постоянной , то говорят, что дисперсия отсутствует. В этом случае частота и волновое число линейно зависимы .

Частота, на которой нормальная волна перестаёт быть распространяющейся, называется частотой запирания. Полагая в дисперсионном уравнении, можно получить уравнение для определения частот запирания.

Рассмотрим распространение волнового пакета с длинами волн, близкими к некоторой длине волны . В этом случае , где , . Тогда

Если дисперсия отсутствует, то заменяем и получаем . Следовательно, в случае отсутствия дисперсии волновой пакет распространяется со скоростью .

Рассмотрим случай, когда дисперсия есть, то есть . Разложим в окрестности в ряд Тейлора:

Обозначим , а и подставим в интеграл:

Следовательно, волновой пакет распространяется со скоростью , называемый групповой скоростью.

2. Постановка задачи

Изучим распространение волн в бесконечном изотропном слое, толщиной . Слой находится в условиях плоского напряжённого состояния.

Введём декартовую систему координат: ось направлена по нормали, а вдоль срединной линии слоя, , .

Выпишем уравнение движения в перемещениях:

где - компоненты вектора перемещения;

- скорость распространения продольной волны в изотропном слое;

- скорость распространения поперечной волны;

Используя формулы Коши, запишем соотношения, связывающие компоненты тензора напряжений и вектора перемещений:

Здесь , , - компоненты тензора напряжений.

Введём безразмерные переменные, безразмерные компоненты вектора перемещений и тензора напряжений; а также безразмерные фазовую скорость и волновое число.

Подставим безразмерные величины в (2.2)

Подставим безразмерные величины в (2.1)

Умножим эти уравнения на

Опустим тильду, тогда уравнения движения в перемещениях (2.1) и граничные условия (2.3), соответственно, примут следующий вид:

Таким образом, требуется найти решение краевой задачи для уравнения(2.4), граничные условия выбираются в зависимости от условий закрепления границ. Рассмотрим простые модельные задачи, а именно, задачу о распространении гармонически х волн в упругом слое со свободными и задачу об определении частот толщинных резонансов.

3. Исследование модельных задач

3.1. Частоты толщинных резонансов

Введём в рассмотрение безразмерные потенциалы поля перемещений , такие, что

Они должны удовлетворять волновым уравнениям:

где - оператор Лапласа. (3.2)

Далее опустим тильду. Используя формулы (2.2), выразим напряжения через потенциалы:

разделим на и опустим тильду

Будем считать, что границы рассматриваемого слоя свободны от напряжений, тогда граничные условия имеют вид:

Частоты толщинных резонансов – это частоты собственных колебаний бесконечно тонких поперечных волокон слоя [3]. В этом случае перемещения не зависят от координаты .

Решение краевой задачи (3.2), (3.4) ищем в виде:

Определим частоты толщинного резонанса растяжения-сжатия. Считаем, что

Тогда из (3.2), (3.4) получим краевую задачу для нахождения функции :

Общее решение уравнения (3.6) имеет вид:

Используя граничные условия, из условия существования нетривиального решения, получим

Отсюда находим частоты толщинного резонанса растяжения-сжатия:

Если перемещение является чётным относительно координаты , то функция должна быть нечётной, и из (3.6), (3.7) можно получить частоты для так называемого антисимметричного напряженного состояния

Если перемещение является нечётным относительно , то - чётная, а частоты толщинного резонанса растяжения сжатия для симметричного напряжённого состояния:

Определим частоты сдвигового толщинного резонанса. Считаем, что

Из (3.2), (3.4) получим краевую задачу для определения функции :

Общее решение задачи (3.13) имеет вид:

Используя граничные условия задачи (3.13), из условия существования нетривиального решения получим:

Длина волны. Скорость волны

За один период волна распространяется на расстояние λ.

λ = vT

Длина волны — это расстояние, на которое распространяется волна за время, равное одному периоду колебаний.

Так как период Т и частота v связаны соотношением

При распространении волны:

1. Каждая частица шнура совершает периодические колебания во времени.
В случае гармонических колебаний (по закону синуса или косинуса) частота и амплитуда колебаний частиц одинаковы во всех точках шнура.
Эти колебания различаются только фазами.

2. В каждый момент времени форма волны повторяется через отрезки длиной λ.

Спустя промежуток времени Δt волна будет иметь вид, изображенный на том же рисунке второй линией.

Для продольной волны также справедлива формула, связывающая скорость распространения волны, длину волны и частоту колебаний.

Все волны распространяются с конечной скоростью. Длина волны зависит от скорости ее распространения и частоты колебаний.

Уравнение гармонической бегущей волны

Вывод уравнения волны, позволяющего определить смещение каждой точки среды в любой момент времени при распространении гармонической волны (на примере поперечной волны, бегущей по длинному тонкому резиновому шнуру).

Ось ОХ направлена вдоль шнура.
Начало отсчета - левый конец шнура.
Смещение колеблющейся точки шнура от положения равновесия - s.
Для описания волнового процесса нужно знать смещение каждой точки шнура в любой момент времени:

s = s (х, t).

Конец шнура (точка с координатой х = 0) совершает гармонические колебания с циклической частотой ω.
Колебания этой точки будут происходят по закону:

s = s_m sinc ωt

Если начальную фазу колебаний считать равной нулю.
s_m — амплитуда колебаний.

Колебания распространяются вдоль оси ОХ со скоростью υ и в произвольную точку с координатой х придут спустя время

Эта точка также начнет совершать гармонические колебания с частотой ω, но с запаздыванием на время τ.

Если пренебречь затуханием волны по мере ее распространения, то колебания в точке х будут происходить с той же амплитудой s_m, но с другой фазой:

Это и есть уравнение гармонической бегущей волны, распространяющейся в положительном направлении оси ОХ.

Используя уравнение можно определить смещение различных точек шнура в любой момент времени.

Механические волны. Физика, учебник для 11 класса - Класс!ная физика

Посмотрев данный видеоурок, учащиеся вспомнят, что называется механической волной и каковы её основные свойства. Мы также поговорим об особенностях распространения волн в упругих средах. Получим уравнение бегущей монохроматической волны. А также рассмотрим некоторые особенности отражения механических волн.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Распространение волн в упругих средах. Уравнение гармонической бегущей волны"

Всё время, пока существует волна, частицы среды совершают колебания около своих положений равновесия и смещаются от него не более чем на амплитуду. При этом различные частицы колеблются со сдвигом по фазе, за исключением тех, положения равновесия которых находятся друг от друга на расстоянии υТ.

Напомним, что геометрическое место точек среды, колеблющихся в одинаковых фазах, образует волновую поверхность.

Волновую поверхность, отделяющую колеблющиеся частицы среды от частиц, ещё не начавших колебаться, называют фронтом волны.

Как отмечалось нами ранее, возмущение, создаваемое источником волны, передаётся от одной точки среды к другой не мгновенно, а с определённой конечной скоростью. Скоростью распространения волны называется физическая величина, определяемая расстоянием, которое проходит любая точка фронта волны за единицу времени.

Для указания направления распространения волн, используется понятие луча. Лучом мы будем называть линию, проведённую перпендикулярно волновому фронту в направлении распространения волны.

Ранее мы с вами показали, что при возбуждении волны происходит процесс распространения колебаний, но не перенос вещества. Следовательно, при распространении волн происходит перенос энергии упругой деформации и импульса без переноса вещества. При этом энергия волны в упругой среде состоит из кинетической энергии совершающих колебания частиц и потенциальной энергии упругой деформации среды.

На прошлом уроке мы с вами говорили о том, что расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны. Она равна тому расстоянию, на которое распространяется волна за период:

Так как период колебаний обратно пропорционален частоте колебаний, то скорость волны связана с частотой колебаний уравнением:

Выразим из этой формулы длину волны, а также воспользуемся связью частоты колебаний с их циклической частотой:

Отсюда видно, что при возникновении волн в среде их частота определяется частотой колебаний источника. А скорость распространения волны зависит от свойств среды. Поэтому волны одной и той же частоты имеют различную длину в разных средах.

Теперь давайте получим уравнение плоской волны, то есть волны, волновые поверхности которой представляют собой плоскости, перпендикулярные к направлению распространения волны.

Предположим, что вибратор совершает гармонические колебания, подчиняющиеся закону синуса (считаем, что начальная фаза колебаний равна нулю):

В записанной формуле s — это смещение колеблющейся точки от положения равновесия, а s_m — амплитуда колебаний.

В точках, отстоящих на расстоянии х от источника, колебания частиц среды волнового фронта будут также гармоническими, с той же частотой, но будут отставать от колебаний источника на время:

Эти точки также начнут также совершать гармонические колебания с той же частотой, но с запаздыванием на время τ. Колебания в точке х будут происходить с той же амплитудой, но с другой фазой:

Это и есть уравнение плоской бегущей монохроматической волны. При этом считают, что в процессе распространения волны её затуханием можно пренебречь. Из уравнения видно, что смещение любой точки среды из равновесного положения при прохождении волны является функцией двух переменных: времени и расстояния до равновесного положения точки среды.

Из этого уравнения также следует, что амплитуда плоской незатухающей волны в данной точке среды постоянна и равна амплитуде колебаний источника. Также видно, что любая точка среды совершает гармонические колебания, начальная фаза которых зависит от удаления данной точки от источника колебаний:

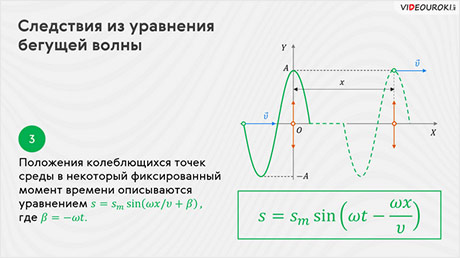
А положения колеблющихся точек среды в некоторый фиксированный момент времени описываются уравнением, которое вы сейчас видите на экране:

А теперь давайте с вами найдём разность фаз колебаний двух точек среды, находящихся на некотором расстоянии друг от друга:

Запишем уравнения, описывающие колебания этих двух точек:

Теперь найдём их разность фаз (напомним, что фазой колебания является аргументом периодической функции):

Перепишем полученное уравнение, воспользовавшись формулой, связывающей циклическую частоту с периодом колебаний:

В знаменателе формулы мы получили произведение периода колебаний и скорости волны, а это, как мы помним, есть длина волны:

Из последнего равенства следует, что если две точки находятся друг от друга на расстоянии длины волны, то разность фаз колебаний этих точек равна 2π, что соответствует данному нами ранее определению длины волны.

Теперь, для закрепления нового материала, давайте решим с вами задачу. Определите частоту звуковых колебаний в воздухе, если расстояние между двумя ближайшими точками волны, отличающимися по фазе на π, составляет 50 см. Для удобства будем считать, что скорость звука равна 340 м/с.

Гармоническая волна — согласно наиболее общему определению — волна, каждая точка колеблющейся среды или поле в каждой точке пространства совершает гармонические колебания [1] . В разных случаях при необходимости особо выделяется интересующий класс гармонических волн, например, плоская гармоническая волна, стоячая гармоническая волна итд (см. ниже).

Слово 'гармоническая' тут является синонимом слова 'монохроматическая', однако, по-видимому, не совсем точным; во всяком случае, обычные области применения того и другого термина обычно несколько различаются.

Источниками гармонических волн могут быть гармонические колебания, они также могут возбуждаться в какой-либо системе при взаимодействии ее с гармонической волной.

Содержание

Одномерный случай

Случай одномерного однородного пространства (или одномерной однородной среды) [2] — наиболее прост.

В этом случае все виды гармонических волн сводятся к:

а также к конечным линейным комбинациям волн такого вида (для выражения произвольной действительной гармонической волн в этом случае достаточно смешать две волны первого вида или четыре второго; в случае более многомерного u добавляется по два таких слагаемых на каждую поляризацию).

Может быть также использовано понятие гармонической стоячей волны, сводящейся к сумме двух гармонических бегущих (бегущих в противоположных направлениях) волн, описанных выше:

Здесь A — постоянный (не зависящий от x и t) коэффициент, природа и размерность которого свпадает с природой и размерностью поля u; k, ω и φ₀ — также постоянные параметры, в рассматриваемом одномерном случае все они — действительные числа (в отличие от более многомерных, где k становится векторным — для плоских волн). A — есть амплитуда волны, k — волновое число, ω — (циклическая) частота и φ₀ — начальная фаза — то есть фаза волны при x = t = 0.

Во второй формуле A — (обычно) комплексное, амплитуду волны определяет его модуль |A|, а начальная фаза спрятана также в A в качестве его аргумента, поскольку

$u(x,t) = A\ e^<i(kx - \omega t)> = |A|\ e^ e^ <i(kx - \omega t)>= |A|\ e^<i(kx - \omega t + Arg A)>.$

Так же, как стоячая волна выражается (как записано здесь) через две бегущих, так же и бегущая может быть выражена через две стоячих. Поэтому можно выбрать один из двух равноправных способов выражения произвольной гармонической волны в случае одномерного однородного пространства: через линейную комбинацию бегущих или линейную комбинацию стоячих волн. Это верно и для всех других случаев, хотя базисные волны, через линейную комбинацию которых выражается произвольная гармоническая волна, могут оказаться сложнее.

случай неоднородного одномерного пространства (неоднородной среды) оказывается значительно сложнее. В этом случае зависимость гармонических волн от пространственной координаты x становится не синусоидальной, а в общем — и наиболее типичном — случае и вовсе не выражается через элементарные функции. Тем не менее, и в этом случае остается верным утверждение о возможности выразить произвольную гамоническую волну через конечное (для определенной частоты) количество базисных гармонических волн.

Случаи пространства размерностью больше единицы

В случаях пространства размерностью больше единицы, даже если оно однородно, в принципе разнообразие возможных гармонических волн очень сильно возрастает. Однако есть два типа гармонических волн, которым следует уделить главное отдельное внимание.

Плоские гармонические волны

наиболее важным и часто встречающимся типом гармонических волн являются плоские гармонические волны. (Одномерные гармонические волны являются их одномерным частным случаем.)

$u(x,t) = A\ e^<i(\vec k \cdot \vec x - \omega t)> ,\$

где, в отличие от одномерной волны — уже не действительное число, а вектор, называемый волновым вектором, размерность которого равна размерности пространства, а выражение означает скалярное произведения этого вектора с вектором [3] , характеризующим точку пространства: .

Легко видеть, что если выбрать ось координат вдоль волнового вектора, плоская многомерная волна сводится к одномерной (u вообще перестает зависеть от остальных координат, а от первой — зависит как одномерная гармоническая волна).

Так же, как и в одномерном случае, стоячие и бегущие гармонические волны одной частоты с одинаковым (быть может, с точностью до знака) волновым вектором, элементарно линейно выражаются друг через друга.

Поскольку с помощью преобразования Фурье (в текущем параграфе подразумевается, конечно, многомерное преобразование Фурье) практически любую [4] функцию пространственных координат можно представить как сумму (интеграл) функций, представляющих каждая плоскую волну, а зависимость от времени в тогда для случая однородного пространства будет тоже очевидно гармонической, то очевидно удобство разложения любой гармонической (да и не только гармонической) волны по плоским гармоническим волнам. В каких-то случаях и в какой-то мере это может быть полезным и в случаях неоднородности пространства, хотя в этом случае это вполне может и не дать ожидаемых преимуществ, или извлечение этих преимуществ может потребовать особого искусства.

Сферические гармонические волны

Сферические гармонические волны несколько менее универсальны и просты (их гораздо труднее даже выписать в явном виде, если не выражать просто через бесконечные суммы/интегралы плоских волн; например, для двумерного пространства гармонические сферические волны выражаются через функции Бесселя, то есть не выражаются через элементарные функции).

Тем не менее они бывают очень полезны, когда сами условия задачи склоняют к попытке рассмотрения сферических волн, то есть, в особенности при исследовании волн, порождаемых точечным источником или когда задача в целом имеет сферическую симметрию (последнее лучше всего для попытки искать решение просто в виде только сферических волн).

Для трехмерного однородного пространства гармонические сферические волны имеют вид:

или (в виде, удобном в качестве для разложения):

" width="" height="" />
" width="" height="" />

Значение и теоретическое применение

Общий линейный случай

Любое линейное дифференциальное уравнение вида

$K \frac<\partial^n u> <\partial t^n>= L u,$

где порядок дифференцирования по времени n может быть любым (чаще интересны n = 1 или 2), а L любой линейный дифференциальный оператор, не зависящий от t (правда, если u должно быть действительным одномерным, а L -эрмитов, то нечетные n придется исключить), будет иметь решением гармоническую волну.

$u = e^<i\omega t> Действительно, подставим \cdot v(x)$
, где x — точка пространства любой размерности. Получаем тогда:

$K i^n\omega^n v = L v,\$

а экспонента сокращается. Сделав такую же подстановку с -ω, получим, при оговоренных выше условиях подходящего K, получить и действительное v как сумму этих двух решений.

Читайте также: