Декодирование линейного кода доклад

Обновлено: 17.05.2024

Пусть V – линейный -код, h – нулевой вектор и h₂, h_{3, …,} h_q k – остальные кодовые векторы. Тогда таблица декодирования можно составить следующим образом. Кодовые векторы располагаются в виде строки с нулевым вектором слева. Затем один из наборов, не содержащийся в этой строке и имеющий разрядность n, например g_i помещается под вектором h. Далее строка заполняется так, чтобы под каждым кодовым вектором h_i помещался вектор . Аналогично в первый столбец очередной строки помещается вектор g₂ и строка заполняется таким же способом. Процесс продолжается до тех пор, пока каждый возможный набор длины n не появится где-нибудь в таблице. Данная таблица называется стандартным расположением и совпадает с таблицей смежных классов.

Теорема 3. Если стандартное расположение используется как таблица декодирования для блокового кода, то по полученному вектору u будет правильно декодирован переданный вектор v тогда и только тогда, когда набор ошибок является образующим смежного класса.

Доказательство: Если , где g_i – образующий i-го смежного класса, то вектор должен находиться в стандартом расположении в i-м смежном классе под кодовым словом u и поэтому будет правильно декодирован. Если же вектор не является образующим смежного класса, то вектор v должен находиться в некотором классе j с образующим g_j. Тогда вектор v расположен в j-й строке, но не под вектором u, потому что .

*0000 *1011 *0101 *1110

1000 0011 1101 0110

0100 1111 0001 1010

0010 1001 0111 1100

а) 1011 ® 1001 ® 1001 (+) 0010 = 1011.

б) 0101 ® 0100 ® 0100 (+) 0100 = 0000 – неверно.

Другим важным случаем декодирования линейных кодов является синдромное декодирование.

Синдромное декодирование.

Предположим, что линейный код является нулевым пространством матрицы H размерности ( )*n. Для любого любого полученного на выходе вектора v вектор с компонентами называется синдромом. Поскольку рассматриваемый код – это нулевое пространство матрицы H, то некоторый вектор является словом тогда и только тогда, когда его синдром равен нулю.

Теорема 4. Два вектора v₁ и v₂ принадлежат одному и тому же смежному классу тогда и только тогда, когда их синдромы равны.

Доказательство: Два элемента группы v₁ и v₂ принадлежат одному и тому же смежному классу тогда и только тогда, когда есть элемент подгруппы, которой в данном случае является кодовое векторное пространство. Если кодовое пространство – это нулевое пространство матрицы H, то вектор принадлежит кодовому пространству тогда и только тогда, когда

Поскольку для умножения матриц справедлив дистрибутивный закон, то

Таким образом, вектор является кодовым вектором тогда и только тогда, когда синдромы векторов v₁ и v₂ равны.

Процесс декодирования может быть значительно упрощен за счет использования модифицированной таблицы декодирования. Таблица строится так, что в ней приводятся образующие смежных классов и синдромы для каждого из 2 n - k смежных классов. После того как получен вектор, вычисляется его синдром. Затем то таблице отыскивается образующий смежного класса, являющийся предполагаемым набором ошибок и вычитается из полученного вектора. В результате образуется предположительно исходный кодовый вектор.

(0000) 1011 0101 1110 (00)

(1000) 0011 1101 0110 (11)

(0100) 1111 0001 1010 (01)

(0010) 1001 0111 1100 (10)

0101®1101®1101 (+) 1000 = 0101

Синдромное декодирование позволяет сократить объем памяти при декодировании. Так, для кода (100,80) необходимо в случае декодировании по лидеру смежного класса 2 100 входов, а в случае синдромного декодирования 2 20 входов.

Коды Хэмминга.

Двоичный код Хэмминга удобнее всего задавать при помощи его проверочной матрицы. Проверочной матрицей кода Хэмминга является матрица, столбцами которой являются все ненулевые наборы разрядности m.

- длина кодового вектора : 2 m -1;

- число проверочных символов : m;

- число информационных символов : /

Поскольку все векторов, задающих одиночные ошибки принадлежат различным смежным классам, то этими смежными классами и кодовым пространством исчерпываются все 2 m смежных классов.

Таким образом, код Хэмминга является совершенным. Линейный код, совокупность образующих смежных классов которого в точности совпадает с совокупностью всех последовательностей веса t или меньше, называется совершенным.

Можно построить код Хэмминга любой длины n, Если выбрать матрицу H для наименьшего значения m, удовлетворяющего условию , а затем отбросить все лишние столбцы, оставив n столбцов. При этом можно выбрать столбцы таким образом, чтобы получился квазисовершенный код.

Добавлением к двоичному коду Хэмминга одного проверочного соотношения, проверяющего на четность совокупность всех символов кода можно получить код с минимальным весом, равным 4, т.е. так называемый расширенный код Хэмминга.

Декодирование такого кода осуществляется следующим образом:

Коды Рида-Маллера.

Достоинства: можно получить большое Хэммингово расстояние и легко поддаются декодированию.

Для любых m и r m , все компоненты которого равны 1, V₁,V₂,…, V_m – строки матрицы, столбцами которой являются все возможные двоичные наборы длины m. Определим следующим образом векторное произведение двух векторов:

Рассмотрим совокупность векторов, образованную произведениями векторов v_i, взятых по два, три, четыре и т.д. вплоть до m.

v₀ = ( 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 )

v₄ = ( 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 )

v₃ = ( 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 )

v₂ = ( 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 )

v₁ = ( 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 )

v₄v₃ = ( 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 )

v₄v₂ = ( 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 1 )

v₄v₁ = ( 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 1 )

v₃v₂ = ( 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 )

v₃v₁ = ( 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 1 )

v₂v₁ = ( 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 )

Код Рида-Маллера порядка r определяется как код, базисом которого являются вектор v₀,v₁,…,v_m и все векторные произведения из r или меньшего числа этих векторов. Очевидно, что скалярное произведение двух векторов равно 0, если число единиц в векторном произведении четно и равно 1, если оно нечетно.

Для любого вектора v v 2 =v. Единственным произведением, содержащим нечетное число единиц, является произведение всех векторов v₁,…,v_m. Векторное произведение любого вектора из базиса кода порядка r на любой вектор из базиса кода порядка m-r-1 является вектором из базиса кода порядка m-1 и в нем содержится четное число единиц. Таким образом, любой вектор, принадлежащий коду порядка r, ортогонален любому базисному вектору, являющемуся произведением m-r-1 или меньшего числа векторов v₁,…,v_m. Из этого также следует, что код Рида-Маллера порядка r является нулевым пространством матрицы, образованной векторами v₀,v₁,…,v_m и всеми векторными произведениями этих векторов в количестве не более чем m-r-1, взятыми в качестве ее строк.

Важнейшая особенность кодов Рида-Маллера состоит в том, что декодирование для них может быть проведено достаточно простым способом.

Информационные символы этого кода кодируются следующим вектором:

Задача состоит в том, чтобы определить значения a по полученному вектору, несмотря на возможные ошибки. Очевидно, что сумма первых четырех компонент как элементов поля из двух элементов (0 и 1) равна нулю для всех базисных векторов, за исключением v₂v₁. Таким образом, если ошибок не было, то:

В общем случае можно записать независимых соотношений. Ошибки могут сделать некоторые из этих соотношений несправедливыми, но каждая ошибка влияет только на одно из соотношений. Следовательно, если выбрать a₂₁ равным величине, появляющейся наиболее часто в выражениях, то при любой комбинации из или меньшего числа ошибок значение a₂₁ будет декодировано правильно. Аналогичным образом определяются a₃₁, a₃₂, a₄₁, a₄₃. После того как они определены, выражение

может быть вычтено из полученного вектора. Тогда, если ошибок не было, останется вектор

так, что следующая совокупность коэффициентов может быть определена аналогичным путём:

Идентичные уравнения можно записать для a₂, a₃, a₄. Если предположить, что ошибок не было, то

Этот вектор должен быть нулевым, если a₀=0 и единичным, если a₀=1, поэтому a₀ нужно выбирать равным тому из этих элементов, который появляется в векторе чаще.

Поскольку при такой системе декодирования могут быть исправлены все комбинации из или меньшего числа ошибок, то минимальное расстояние должно быть равно самое меньшее , а так как все кодовые векторы имеют четный вес, то оно должно быть равно самое меньшее .

Схему для определения того, суммы каких именно символов полученного вектора должны быть равны заданному информационному символу, можно описать следующим образом. Расположим символы в каждом из первоначальных векторов v₁,…,v_m, и назовем компоненту, соответствующую j-ому нулю в векторе v_i, и компоненту, соответствующую j-ой единице в векторе v_i, парными компонентами вектора v_i. Тогда 2 ( m -1) сумм парных компонент v_i используются для определения a_i. Далее, каждая из 2 ( m -2) сумм четырех компонент, используемых для определения a_ij, образуется некоторыми двумя парными компонентами вектора v_i и парными для этих уже выбранных компонент компонентами вектора v_j. Аналогично каждое соотношение, определяющее a_ijk, представляет собой сумму некоторых парных компонент вектора v_i плюс сумму компонент вектора v_j, парных к этим компонентам, и сумму компонент вектора v_k, парных к уже выбранным компонентам, так, что в каждой сумме получается всего 8 слагаемых. Этот процесс можно продолжить аналогичным образом.

Путь - матрица размера и ранга над полем . Эта матрица задает линейное отображение B^" />
пространства в пространство " />
по формуле . Ядро этого линейного отображения или множество решений уравнения , образующее подпространство пространства , является линейным кодом . Можно рассмотреть разбиение пространства на классы равнообразности. В один класс входят все элементы , которые при отображении B^" />
переходят в один и тот же элемент пространства " />
. Элемент пространства " />
, в который переходят все элементы одного класса, называется синдромом. Pис.7.8 иллюстрирует разбиение пространства на классы равнообразности.

Отображение B^" />
является отображением на все пространство " />
. Для систематической матрицы H это практически очевидно. Действительно, для любого " />
можно найти (построить) , такой, что .

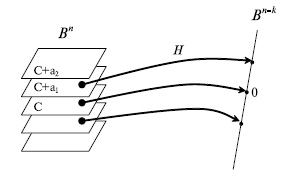
Рис. 7.8. Разбиение пространства Bn на классы равнообразности

Произведение называется синдромом [29], [33]. Фактически, синдромом вектора является образ этого вектора при отображении - B^" />
. Все векторы , имеющие один синдром, образуют класс . Так как синдром " />
имеет размерность , всего существует " />
классов (если проверочная матрица имеет ранг , в частности, если матрица имеет систематический вид). Из определения линейного кода следует, что класс , которому соответствует нулевой синдром, является кодом . Каждый класс , отличный от кода, порождается "сдвигом" кода на один из векторов класса . Действительно, если ., то есть , тогда и, следовательно, и , где - кодовое слово . Таким образом, любой некодовый вектор , имеющий синдром , можно представить в виде суммы кодового вектора и вектора, имеющего синдром . Представление такого вида не является единственным. Некодовый вектор в этой сумме можно рассматривать как вектор ошибок, произошедших в тех разрядах кодового слова , в которых соответствующие компоненты вектора равны 1. Из всех векторов ошибок, имеющих один синдром, наиболее вероятным является вектор (векторы) с минимальным весом (числом единичных компонент ). Такой вектор (векторы) называется лидером класса.

Алгоритм декодирования заключается в следующем. Если получен вектор и , считаем, что ошибкам соответствует наиболее вероятный вектор из класса , то есть лидер класса . Тогда декодирование осуществляется в вектор , получающийся из принятого вектора удалением лидера.

$\begin x_1+x_2+x_3=0\\x_1+x_4=0\end\Rightarrow \beginx_3=x_1+x_2\\x_4=x_1\end$

и которые можно рассматривать как информационные разряды, задаются произвольно (всего 4 варианта 00, 01, 10, 11), а проверочные разряды и определяются через и . В итоге все кодовые слова определяются из выражения

$\begin x_1\\x_2\\x_3\\x_4\end=\begin1&0\\0&1\\1&1\\1&0\end*,$

где и - информационные разряды, а 1&0\\0&1\\1&1\\1&0\end" />
- порождающая матрица , столбцами которой являются кодовые векторы.

Кодовые слова, рассматриваемые как векторы-столбцы, образуют матрицу кода

$C=\begin 0&0&1&1\\ 0&1&0&1\\ 0&1&1&0\\ 0&0&1&1\end$

Расстояние кода равно минимальному весу ненулевого слова .

Найдем смежные классы, которые состоят из векторов пространства , имеющих одинаковый синдром, и выберем в каждом классе лидера ( вектор из класса с минимальным весом).

Синдромом является любое возможное значение произведения .

В данном случае имеется 4 синдрома: , , , " />
.Каждому синдрому соответствует смежный класс , синдром " />
соответствует коду. Смежные классы (столбцы матриц) для каждого синдрома и выбранные лидеры приведены в таблице.

В третьем смежном классе - два потенциальных лидера с весом (нормой), равным 1. Один из них выбирается в качестве лидера произвольно.

Рассмотрим на этом примере процесс декодирования полученного вектора (слова) с использованием синдромов. Пусть передавался кодовый вектор 0\\1\\1\\0\end" />
и в процессе переачи произошла ошибка в первом разряде. Это означает, что на приемном конце был получен вектор 1\\1\\1\\0\end=\begin0\\1\\1\\0\end+\begin1\\0\\0\\1\end" />
, полученный из переданного вектора 0\\1\\1\\0\end" />
в результате добавления вектора ошибки 1\\0\\0\\0\end" />
(ошибка в первом разряде). Определим синдром, вычислив произведение . В данном случае получим " />
. Это означает, что полученный вектор водит в четвертый смежный класс (см. таблицу). Лидером этого смежного класса является вектор 1\\0\\0\\0\end" />
, соответствующий данному синдрому. Вычитая (добавляя) лидер к принятому вектору, производим декодирование 0\\1\\1\\0\end" />
В данном случае декодирование выполнено правильно.

В данной публикации будет рассматриваться линейно групповой код, как один из представителей систематических корректирующих кодов и предложена его реализация на C++.

Что из себя представляет корректирующий код. Корректирующий код – это код направленный на обнаружение и исправление ошибок. А систематические коды — Это коды, в которых контрольные и информационные разряды размещаются по определенной системе. Одним из таких примеров может служить Код Хэмминга или собственно линейно групповые коды.
Линейно групповой код состоит из информационных бит и контрольных. Например, для исходной комбинации в 4 символа, линейно групповой код будет выглядеть вот так:

Где первые 4 символа это наша исходная комбинация, а последние 3 символа это контрольные биты.

Общая длина линейно группового кода составляет 7 символов. Если число бит исходной комбинации нам известно, то чтобы вычислить число проверочных бит, необходимо воспользоваться формулой:

Где n — это число информационных бит, то есть длина исходной комбинации, и log по основанию 2. И общая длина N кода будет вычисляться по формуле:

Допустим исходная комбинация будет составлять 10 бит.

d всегда округляется в большую сторону, и d=4.

И полная длина кода будет составлять 14 бит.

Разобравшись с длиной кода, нам необходимо составить производящую и проверочную матрицу.

Линейно групповой код: 100110101011100

Сразу обозначим, что контрольные разряды в ЛГК определяются по правилам чётности суммы соответствующих индексов, в нашем случае, эти суммы составляют: 5,3,3,4,4. Следовательно, контрольная часть кода выглядит: 11100.

Допустим, наш код был отправлен с ошибкой в 6-ом разряде. Для определения ошибок в коде служит, уже ранее составленная проверочная матрица

В нашем случае синдром равен: 01111, что соответствует 6-му разряду в ЛГК. Мы инвертируем бит и получаем корректный линейно групповой код.

Декодирование скорректированного ЛГК происходит путём простого удаления контрольных бит. После удаления контрольных разрядов ЛГК мы получаем исходную комбинацию, которая была отправлена на кодировку.

В заключение можно сказать, что такие корректирующие коды как линейно групповые коды, Код Хэмминга уже достаточно устарели, и в своей эффективности однозначно уступят своим современным альтернативам. Однако они вполне справляются с задачей познакомиться с процессом кодирования двоичных кодов и методом исправления ошибок в результате воздействия помех на канал связи.

Реализация работы с ЛГК на C++:

3. Тенников, Ф.Е. Теоретические основы информационной техники / Ф.Е. Тенников. – М.: Энергия, 1971. – 424 с.

Теоретическая часть.
Дискретный канал.

кратность гарантированно обнаруживаемых ошибок;

кратность гарантированно исправляемых ошибок.

Под избыточностью понимают число вводимых дополнительных разрядов

где n — число кодовых символов на выходе кодера, соответствующих k информационным символам на его входе.
Кодовое расстояние d или расстояние характеризует степень различия любых двух кодовых комбинаций. Оно выражается числом разрядов, в которых комбинации отличаются одна от другой.

Для помехоустойчивого кода наиболее важным является минимальное кодовое расстояние - наименьшее кодовое расстояние из всех между всеми парами кодовых комбинаций.
В общем случае при необходимости обнаруживать ошибки кратности минимальное кодовое расстояние должно быть, по крайней мере, на единицу
больше , т. е.
Соответственно, кратность гарантированно обнаруживаемых кодом ошибок равна

Кратность гарантированно исправляемых кодом ошибок вычисляется по формуле

Таким образом, код, имеющий минимальное кодовое расстояние ,

Рис.2. Общий принцип исправления и обнаружения ошибок.

В случае, если по каналу было передано кодовое слово , и оно пришло с искажениями, возможны три варианта декодирования с исправлением ошибки.
1. Было получено слово, попадающее в область вокруг вектора . Такое слово будет преобразовано декодером в слово и декодирование будет осуществлено верно.

Если получено слово, не принадлежащее областям ни одного кодового слова, то оно не может быть декодировано и, следовательно, возникает ошибка декодирования.

3. Слово, попадающее в область вокруг , будет преобразовано декодером в .
Такая ошибка не может быть обнаружена.
В показанном на рис. 5.1 случае не все слова размерности n принадлежат областям декодирования. Таких кодов большинство. Коды, в которых непересекающиеся области декодирования охватывают все пространство слов размерности n, называются совершенными или плотноупакованными. При использовании совершенных кодов всегда возможна коррекция ошибок (не всегда правильная). Декодер такого кода не может определить ошибку декодирования. Он работает либо в режиме определения ошибок, либо в режиме исправления ошибок. Основными совершенными кодами являются коды Хэмминга и коды Голея.
Код Хэмминга можно построить для любого натурального числа r ≥ 3. Этот код будет обладать рядом свойств.

n=2r-1
k=2r-1-r
r=n-k
d_min=3, t=1

v=u₀v₀+u₁v₁+…+u_k_-1v_k_-1,(1)

Векторы базиса образуют порождающую матрицу G размера

Тогда уравнение (1) принимает вид

v=uG(2)

где u=(u₀,u₁, u_k_-1) - информационное слово.
Фактически, формула (36) описывает процедуру кодирования линейного блочного кода посредством образующей матрицы. Для пространства кодовых слов линейного (n,k)-кода существует дуальное ему пространство кода (n,n−k), порождаемое матрицей H размера (n−k)×n. Такая матрица получила название проверочной для кода (n,k) и обладает следующими свойствами
GH T =0 (3)

vH T =0

на основе которых реализована операция декодирования линейных блочных кодов.
Как правило рассматривают так называемые систематические или каноничные формы матриц G и H, использующиеся для процедуры систематического кодирования. На практике, любая порождающая матрица G линейного блочного (n,k)-кода может быть преобразована к систематическому виду посредством элементарных операций и перестановок столбцов матрицы.
Матрица G в систематической форме состоит из двух подматриц: единичной матрицы I размера k×k и проверочной подматрицы P размера k×(n−k) .

Соответственно, исходя из свойства (3), следует, что проверочная матрица H состоит из транспонированной проверочной матрицы и единичной матрицы размера .

Декодирование линейных блочных кодов.
Как и в случае кодирования, декодирование линейных блочных кодов можно осуществлять посредством таблицы по принципу максимального правдоподобия. В этом случае производится последовательное поразрядное сравнение принятого на вход декодера слова со всеми возможными кодовыми словами. В результате будет выбрано кодовое слово, имеющее наименьшее число отличий от декодируемого. В случае несовершенных кодов возможен вариант, когда есть несколько кодовых слов, отличающихся от принятого в одинаковом числе разрядов. Соответственно, декодер

не может принять решение о верности одного из вариантов и выдает сигнал о невозможности декодирования. Недостатки такой схемы те же, что и в случае кодирования - необходим большой объем памяти для хранения всех кодовых слов в случае длинных кодов. Быстродействие для длинных кодов также значительно увеличивается.
В связи с этим используют механизм синдромного декодирования, основанный на использовании проверочной матрицы H.
Для понимания принципа декодирования рассмотрим как выражаются проверочные символы кодового слова через информационные на примере систематического кода Хэмминга (7,4).

Если в канале произошла ошибка, то для принятого вектора r хотя бы одно из равенств (4) выполняться не будет. Проверочные соотношения можно записать для принятого вектора в виде системы уравнений (4).

Соответственно, если хотя бы один из компонент вектора s = < , , >не равен нулю, то в принятом слове есть ошибка.
Уравнения (5) можно записать через проверочную матрицу H.

Вектор s принято называть синдромом. Таким образом, ошибка в принятом слове будет обнаружена, если хоть один компонент синдрома принятого слова не равен нулю. Для исправления ошибки используется тот факт, что каждый синдром соответствует своей позиции одиночной ошибки (мы говорим о кодах Хэмминга).
Расширенные коды Хэмминга.
Расширение кода Хэмминга заключается в дополнении кодового слова дополнительным двоичным разрядом так, чтобы оно содержало четное число единиц. Такое расширение дает ряд преимуществ.

Длина кода увеличивается до n = 2r, что удобнее для хранения и передачи информации.

2. Минимальное расстояние = 4, следовательно = 3.
Также, дополнительный разряд позволяет использовать декодер в гибридном режиме обнаружения и коррекции ошибок.

Практическая часть.
Техническое задание: Написать программу для реализации кодирования и декодирования помехоустойчивым кодом Хемминга.
Исходные данные:
Порождающая матрица G:

Проверочная матрица H:

Текст для кодирования:
One of the most alarming forms of air pollution is acid rain. It results from the release into the atmosphere of sulphur and nitrogen oxides that react with water droplets and return to earth in the form of acid rain, mist or snow.
Acid rain is killing forests in Canada, the USA, and central and northern Europe. (Nearly every species of tree is affected.) It has acidified lakes and streams and they can’t support fish, wildlife, plants or insects. (In the USA 1 in 5 lakes suffer from this type of pollution).

Листинг программы.

Результаты работы программы.

Рис.3. Интерфейс программы.

Рис.4. Результаты кодирования.

Смоделируем действие шума в двоичном канале, изменив произвольным образом N символов:

Шифр до внесения изменений:
01000111 11111111
01101100 11100010
01101100 01011010
00101011 00000000
01101100 11111111
01101100 01101100
00101011 00000000
01110001 01000111
01101100 10001110
01101100 01011010

Шифр после внесения изменений:
01001111 11111111
01101100 11100010
11101100 01011010
00101011 00010000
01101100 11111111
01101000 01101100
00101011 00000000
01110001 11010111
01101100 10001110
01101101 01011010

Рис.5.

Рис.6. Результаты декодирования.

Читайте также: